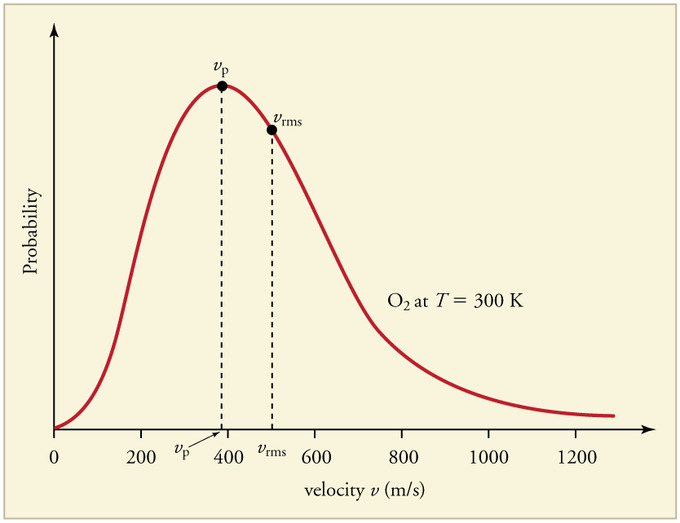
\(T_{boom}\) being nuclear suggests that energy is generated in excess of energy input driving the matter to higher temperature. The velocities \(v\) of individual particles are, if we admit Kinetic Theory for ideal gas, distributed according to the Maxwell-Boltzmann distribution. The most probable velocity \(v_{p}\) is given by,
\(v_{p}=\sqrt{\cfrac{2RT}{M_m}}\) --- (*)
where \(T\), is the temperature when most particles attain \(v_{p}\)
If at \(v_{p}\), the particles are in resonance (post "A Small Boom" dated 16 Oct 2017) and is nuclear, then \(T_{boom\,p}\) is the temperature when the matter is most nuclear, probablistically.
\(v^2_{p}=\cfrac{2RT}{M_m}\)
but,
\(v^2_{rms}=\cfrac{3RT_{rms}}{M_m}=\cfrac{3}{2}v^2_{p}\)
If we set, \(v_{p}=v_{boom}\), then
\(v^2_{rms}=\cfrac{3}{2}v^2_{p}=\cfrac{3}{2}v^2_{boom}\)
and
\(T_{boom\,p}=T_{rms}=v^2_{rms}.\cfrac{M_m}{3R}=\cfrac{3}{2}v^2_{boom}.\cfrac{M_m}{3R}=\cfrac{3}{2}T_{boom}\)
Boiling or melting may not require the matter to be at its most nuclear. Sufficient energy to initiate a change in phase will do.
However, the rms value is likely the measured value of \(T\), as the average energy (root of the mean square value) content of the whole distribution profile. However, energy radiating from the matter will peak when \(v_{boom}\) is most probable, and so, when \(T=T_{boom\,p}\) the matter is most nuclear. Or simply from (*)
\(T_{boom\,p}=v^2_{boom}.\cfrac{M_m}{2R}\)
when \(v_{boom}=v_{p}\)
And we have to adjust all values of \(T_{boom}\) calculated previously.