Cesium lead tribromide (\(CsPbBr_3\)) perovskite nanocrystals,\(Z_m=55+82+35*3\), with density \(4.83\,gcm^{-3}\), and molar mass (calculated) \(579.82\,gmol^{-1}\),
\(v_{boom}=3.4354*\cfrac{4830}{55+82+35*3}=68.57\,ms^{-1}\)
\(T_{boom}=68.57^2*\cfrac{579.82*10^{-3}}{2*8.3144}=163.95\,K\) or \(-109.20^oC\)
By themselves these values are not indicative.
Wednesday, November 29, 2017
Tuesday, November 28, 2017
Monday, November 27, 2017
Freeze! Police
What happens when,
\(f_{\psi}=\cfrac{c}{2\pi a_\psi}=\cfrac{c}{2\pi*14.77}=3230699.3\,GHz\)
hits you?
You freeze。 唛唷!定哋唻。
Why is the phase already at \(\pi\) or negative? Time particles is ejected from the center of all \(a_{\psi\,c}\) (post "Sticky Particles Too...Many" dated 24 Jun 2016), energy density, \(\psi\) is lost, and we experience the passage of time. This frequency pointing at an object, returns the \(\psi\) lost and time stand still.
Maybe...but definitely 打劫!!!
No, just robbing time, suspended animation and long space flight...and who else wants your head frozen.
\(f_{\psi}=\cfrac{c}{2\pi a_\psi}=\cfrac{c}{2\pi*14.77}=3230699.3\,GHz\)
hits you?
You freeze。 唛唷!定哋唻。
Why is the phase already at \(\pi\) or negative? Time particles is ejected from the center of all \(a_{\psi\,c}\) (post "Sticky Particles Too...Many" dated 24 Jun 2016), energy density, \(\psi\) is lost, and we experience the passage of time. This frequency pointing at an object, returns the \(\psi\) lost and time stand still.
Maybe...but definitely 打劫!!!
No, just robbing time, suspended animation and long space flight...and who else wants your head frozen.
Just A Strobe Light
Consider,
\(2cos^2(\cfrac{\phi}{2})=cos(\phi)+1\lt cos(\phi)+v\)
when \(v\lt1\),
\(2cos^2(\cfrac{\phi}{2})\lt cos(\phi)+v\)
because of the power of two, \(\phi\) has a period of \(\pi\) and \(\cfrac{\phi}{2}\) has a period of \(\cfrac{\pi}{2}\)
Given, \(v\lt1\), \(\cfrac{\phi}{2}\lt \cfrac{\pi}{2}\) and let \(\theta=\cfrac{\phi}{2}\)
From the post "Moving Moving...Frames" dated 25 Nov 2017,
\(\theta\lt \cfrac{\pi}{2}\)
The \(x\) axis is marked by the zeros of \(cos^2(\theta)\), and \(x=cos(\phi)+v\) the zeros of \(cos(\phi)+1\) and \(cos^2(\theta)\) are the same. Since \(\theta\lt \cfrac{\pi}{2}\), it takes at least two \(\theta\)s for \(x\) to be along \(VO\) and \(x\) stands still. Two more \(\theta\)s and \(x\) is in the reverse direction \(OH\). \(x\) is a vector, it is pointing left. \(v\) varies with each turn of \(\theta\).
In this case \(\theta\) or \(\cfrac{\phi}{2}\) is changed by adding \(v\), a moving reference frame with velocity \(v\). If \(\theta\) is changed directly, as in the case of a pulsing light by changing its flash frequency, then \(\theta\) is not restricted to be less then \(\cfrac{\pi}{2}\). As \(\theta\) is increased from zero, \(x\) stands still when \(\theta=\cfrac{\pi}{2}\), and then seems to reverse at \(\theta=\pi\).
If \(x\) are marked by the blades of a fan swinging by periodically, first the blades seem to stand still and then reverses its direction, as the flash frequency increases.
This form of time travel/reversal, requires "presence" at the furthest point back in time, traveled to. This is the origin. Time reversal cannot be further back beyond this origin.
Which is just like making a video and then reversing it, except you have no participation; the reversed playback is not real.
In this case, the motion is periodic in the first place. The same motion is repeated over and over.
Just a strobe light...except for,
\(f_{\psi}=\cfrac{c}{2\pi a_\psi}=\cfrac{c}{2\pi*14.77}=3230699.3\,GHz\)
from the post "A Treasure What Worth?" dated 30 Jul 2016. \(a_{\psi}=14.77\,nm\) is the time particle exerting a placid field (post "The Placid Field" dated 30 Jul 2016). This frequency may just make it real.
Note: The direction of \(x\) is reversed from the post "Moving Moving...Frames" dated 25 Nov 2017, such that \(\theta\) is the angle the resultant vector (\(x+v\)) makes with \(x\). If the other direction of \(x\) is considered then the resultant angle will be \(\cfrac{\pi}{2}-\theta\) and the end result is the same.
Remember alien experiment where the candle flame freezes in the (time) field?
\(2cos^2(\cfrac{\phi}{2})=cos(\phi)+1\lt cos(\phi)+v\)
when \(v\lt1\),
\(2cos^2(\cfrac{\phi}{2})\lt cos(\phi)+v\)
because of the power of two, \(\phi\) has a period of \(\pi\) and \(\cfrac{\phi}{2}\) has a period of \(\cfrac{\pi}{2}\)
Given, \(v\lt1\), \(\cfrac{\phi}{2}\lt \cfrac{\pi}{2}\) and let \(\theta=\cfrac{\phi}{2}\)
From the post "Moving Moving...Frames" dated 25 Nov 2017,
\(\theta\lt \cfrac{\pi}{2}\)
The \(x\) axis is marked by the zeros of \(cos^2(\theta)\), and \(x=cos(\phi)+v\) the zeros of \(cos(\phi)+1\) and \(cos^2(\theta)\) are the same. Since \(\theta\lt \cfrac{\pi}{2}\), it takes at least two \(\theta\)s for \(x\) to be along \(VO\) and \(x\) stands still. Two more \(\theta\)s and \(x\) is in the reverse direction \(OH\). \(x\) is a vector, it is pointing left. \(v\) varies with each turn of \(\theta\).
In this case \(\theta\) or \(\cfrac{\phi}{2}\) is changed by adding \(v\), a moving reference frame with velocity \(v\). If \(\theta\) is changed directly, as in the case of a pulsing light by changing its flash frequency, then \(\theta\) is not restricted to be less then \(\cfrac{\pi}{2}\). As \(\theta\) is increased from zero, \(x\) stands still when \(\theta=\cfrac{\pi}{2}\), and then seems to reverse at \(\theta=\pi\).
If \(x\) are marked by the blades of a fan swinging by periodically, first the blades seem to stand still and then reverses its direction, as the flash frequency increases.
This form of time travel/reversal, requires "presence" at the furthest point back in time, traveled to. This is the origin. Time reversal cannot be further back beyond this origin.
Which is just like making a video and then reversing it, except you have no participation; the reversed playback is not real.
In this case, the motion is periodic in the first place. The same motion is repeated over and over.
Just a strobe light...except for,
\(f_{\psi}=\cfrac{c}{2\pi a_\psi}=\cfrac{c}{2\pi*14.77}=3230699.3\,GHz\)
from the post "A Treasure What Worth?" dated 30 Jul 2016. \(a_{\psi}=14.77\,nm\) is the time particle exerting a placid field (post "The Placid Field" dated 30 Jul 2016). This frequency may just make it real.
Note: The direction of \(x\) is reversed from the post "Moving Moving...Frames" dated 25 Nov 2017, such that \(\theta\) is the angle the resultant vector (\(x+v\)) makes with \(x\). If the other direction of \(x\) is considered then the resultant angle will be \(\cfrac{\pi}{2}-\theta\) and the end result is the same.
Remember alien experiment where the candle flame freezes in the (time) field?
Barium And Green
Barium is interesting with \(Z_m=56\), density \(3.51\,gcm^{-3}\) and molar mass \(137.327\,gmol^{-1}\)
\(v_{boom}=3.4354*\cfrac{3510}{56}=215.33\,ms^{-1}\)
\(T_{boom}=215.33^2*\cfrac{137.327*10^{-3}}{2*8.3144}=382.90\,K\) or \(109.75\,^oC\)
Does it glow green at \(T_{boom}=109.75\,^oC\)? Explosive! And poisonous!
\(v_{boom}=3.4354*\cfrac{3510}{56}=215.33\,ms^{-1}\)
\(T_{boom}=215.33^2*\cfrac{137.327*10^{-3}}{2*8.3144}=382.90\,K\) or \(109.75\,^oC\)
Does it glow green at \(T_{boom}=109.75\,^oC\)? Explosive! And poisonous!
Saturday, November 25, 2017
Moving Moving...Frames
OMG it is possible to go back to the rest frame by moving in the moving frame that moves in a moving frame... for eight times.
where geometrically, \(\theta=45^{o}\) and \(v=x\), \(v'=x'\), \(v"=x"\)...
What does this mean?!
where geometrically, \(\theta=45^{o}\) and \(v=x\), \(v'=x'\), \(v"=x"\)...
What does this mean?!
Both Frames Moving Linearly...
And if both reference frames are moving,
From the post "Thought Experiment Gone Wrong" dated 17 Nov 2017,
\(x^{'}=\cfrac{x-vt}{\sqrt{1-v^2}}\)
So,
\(x^{''}=\cfrac{x^{'}-v^{'}t}{\sqrt{1-{v^{'}}^{2}}}\)
It is tempting to substitute one into the other, and get
\(x^{"}=\cfrac{\cfrac{x-vt}{\sqrt{1-v^2}}-v^{'}t}{\sqrt{1-{v^{'}}^{2}}}\)
in this case, \(v^{'}\) is the speed measured in \(x^{'}\) frame not \(x\). Every unit in \(x^{'}\) as measured in \(x\) is scaled by the factor \(\cfrac{1}{\sqrt{1-v^2}}\). Instead we should have,
\(x^{"}=\cfrac{{x-vt}-v^{'}t}{\sqrt{({1-v^2})(1-{v^{'}}^{2})}}=\cfrac{x-(v+v^{'})t}{\sqrt{({1-v^2})(1-{v^{'}}^{2})}}\)
where \(v^{'}\) is also scaled by \(\cfrac{1}{\sqrt{1-v^2}}\),
\(v^{'}\rightarrow \cfrac{v^{'}}{\sqrt{1-v^2}}\).
Do we scale \(v^{'}\) again in the denominator? No. The scaling factor from \(x^{"}\) to \(x^{'}\) does not get scaled again. The translation term get scaled.
Just for the fun of it...
From the post "Thought Experiment Gone Wrong" dated 17 Nov 2017,
\(x^{'}=\cfrac{x-vt}{\sqrt{1-v^2}}\)
So,
\(x^{''}=\cfrac{x^{'}-v^{'}t}{\sqrt{1-{v^{'}}^{2}}}\)
It is tempting to substitute one into the other, and get
\(x^{"}=\cfrac{\cfrac{x-vt}{\sqrt{1-v^2}}-v^{'}t}{\sqrt{1-{v^{'}}^{2}}}\)
in this case, \(v^{'}\) is the speed measured in \(x^{'}\) frame not \(x\). Every unit in \(x^{'}\) as measured in \(x\) is scaled by the factor \(\cfrac{1}{\sqrt{1-v^2}}\). Instead we should have,
\(x^{"}=\cfrac{{x-vt}-v^{'}t}{\sqrt{({1-v^2})(1-{v^{'}}^{2})}}=\cfrac{x-(v+v^{'})t}{\sqrt{({1-v^2})(1-{v^{'}}^{2})}}\)
where \(v^{'}\) is also scaled by \(\cfrac{1}{\sqrt{1-v^2}}\),
\(v^{'}\rightarrow \cfrac{v^{'}}{\sqrt{1-v^2}}\).
Do we scale \(v^{'}\) again in the denominator? No. The scaling factor from \(x^{"}\) to \(x^{'}\) does not get scaled again. The translation term get scaled.
Just for the fun of it...
Seeding Clouds
What is the temperature of thunderstorm clouds, where the lightning has been? It is possible to seed the clouds simply with water at \(\approx80^oC\).
If water is sprayed, it will have to be hotter at the nozzle such that the fine mist that forms at the end of its trip is at \(80^oC\).
What you would see is lightning, as the spray mixes with the clouds.
Sing!
If water is sprayed, it will have to be hotter at the nozzle such that the fine mist that forms at the end of its trip is at \(80^oC\).
What you would see is lightning, as the spray mixes with the clouds.
Sing!
Lightning Generator
This is a lightning generator,
water at the density of \(971.8\,kgm^{-3}\) (at \(80^oC\) or with a suspension/air mix to achieve this density) contained and stirred at \(v=r\omega=333.85\,ms^{-1}\), \(r\) being half the blade width. The blades are insulated at the axial.
If water does disintegrate at this velocity, many particles both positive and negative will be generated.
How to separate them? These particles must be conducted away, if not this is a bomb not a generator.
water at the density of \(971.8\,kgm^{-3}\) (at \(80^oC\) or with a suspension/air mix to achieve this density) contained and stirred at \(v=r\omega=333.85\,ms^{-1}\), \(r\) being half the blade width. The blades are insulated at the axial.
If water does disintegrate at this velocity, many particles both positive and negative will be generated.
How to separate them? These particles must be conducted away, if not this is a bomb not a generator.
Lightning Is Nuclear
Hydrogen, \(H_2\), with \(Z_m=2\), density \(0.08988\,gL^{-1}\), molar mass \(1.00784\,gmol^{-1}\)
\(v_{boom}=3.4354*\cfrac{0.08988}{1*2}=0.154\,ms^{-1}\)
\(T_{boom}=0.154^2*\cfrac{1.00784*10^{-3}}{2*8.3144}=1.44e-6\,K\)
This is way low, practically at zero Kelvin.
Water at \(80^oC\), with a density of \(971.8\,kgm^{-3}\),
\(v_{boom\,water}=3.4354*\cfrac{971.8}{10}=333.85\,ms^{-1}\)
Which is about lightning speed of \(332\,ms^{-1}\). Is lightning nuclear? What raise water temperature to \(80\,^oC\) in the first place? Density of condensed water droplets in the air could change with air currents to \(971.8\,kgm^{-3}\) without an increase in temperature. It is just mixing air into water to bring down the density of water.
\(v_{boom}\) causes the lightning to race at \(v_{boom}\) speed after initiation because the particles exit/separate at \(v_{boom}\) speed (post "Sonic Boom" dated 14 Oct 2017 and post "No Solution But Exit Velocity Anyway" dated 14 Jul 2015). But, how does lightning start?
Given temperature, the spread of velocities (Boltzmann distribution) among the water molecules provides that some are at \(v_{boom}\) speed. Given similar water density across wide region, lightning can propagate from end to end.
The waiting factor is for condensed water in the clouds to be at the right density of \(971.8\,kgm^{-3}\).
Goodnight.
\(v_{boom}=3.4354*\cfrac{0.08988}{1*2}=0.154\,ms^{-1}\)
\(T_{boom}=0.154^2*\cfrac{1.00784*10^{-3}}{2*8.3144}=1.44e-6\,K\)
This is way low, practically at zero Kelvin.
Water at \(80^oC\), with a density of \(971.8\,kgm^{-3}\),
\(v_{boom\,water}=3.4354*\cfrac{971.8}{10}=333.85\,ms^{-1}\)
Which is about lightning speed of \(332\,ms^{-1}\). Is lightning nuclear? What raise water temperature to \(80\,^oC\) in the first place? Density of condensed water droplets in the air could change with air currents to \(971.8\,kgm^{-3}\) without an increase in temperature. It is just mixing air into water to bring down the density of water.
\(v_{boom}\) causes the lightning to race at \(v_{boom}\) speed after initiation because the particles exit/separate at \(v_{boom}\) speed (post "Sonic Boom" dated 14 Oct 2017 and post "No Solution But Exit Velocity Anyway" dated 14 Jul 2015). But, how does lightning start?
Given temperature, the spread of velocities (Boltzmann distribution) among the water molecules provides that some are at \(v_{boom}\) speed. Given similar water density across wide region, lightning can propagate from end to end.
The waiting factor is for condensed water in the clouds to be at the right density of \(971.8\,kgm^{-3}\).
Goodnight.
Friday, November 24, 2017
Hot Superconductor, Cold Superconductor
This is impossible, \(BaTiO_3\),
\(v_{boom}=3.4354*\cfrac{6020}{56+22+8*3}=202.76\,ms^{-1}\)
\(T_{boom}=202.76^2*\cfrac{233.192*10^{-3}}{2*8.3144}=576.50\,K\) or \(303.35\,^oC\)
This is way hot. Temperature is know to decrease conductivity. An impossible hot superconductor.
For \(CaCu_3Ti_4O_{12}\),
\(v_{boom}=3.4354*\cfrac{4700}{20+29*3+22*4+8*12}=55.49\,ms^{-1}\)
\(T_{boom}=55.49^2*\cfrac{614.1789*10^{-3}}{2*8.3144}=43.17\,K\) or \(-229.98\,^oC\)
This is cold. The cell unit is too big to be considered as a quasi-nucleus. Maybe it is possible to parcel out molar mass and arrive at a density value for copper only in the crystal structure.
\(f_{Cu}=\cfrac{total\,molar\,mass\,Cu}{total\,atomic\,molar\,mass}\)
\(M_{m\,Cu}=M_m*f_{Cu}\approx molar\,mass\,Cu\)
where \(M_m\) is molecular mass,
\(\rho_{cu}=\rho_{m}.f_{cu}\)
where \(\rho_{m}\) and \(\rho_{cu}\) are crystal density and density of \(Cu\) in the structure, and so consider only copper in the structure.
So,
\(f_{Cu}=\cfrac{63.546*3}{614.1789}=0.310\)
\(\rho_{cu}=4700*0.310=1458.86\,kgm^{-3}\)
Considering only \(Cu\) in \(CaCu_3Ti_4O_{12}\),
\(v_{boom}=3.4354*\cfrac{1458.86}{29*3}=57.60\,ms^{-1}\)
\(T_{boom}=57.60^2*\cfrac{63.546*3*10^{-3}}{2*8.3144}=38.03\,K\)
It does not seem to work. Furthermore, to consider collisions with \(Cu\) only, the atomic will have to dominate the structure in size. The rest of the molecules is as if does not exist. Even so, three separate \(Cu\) atoms does not form a quasi-nucleus. Maybe,
\(v_{boom}=3.4354*\cfrac{1458.86}{29}=172.82\,ms^{-1}\)
\(T_{boom}=172.82^2*\cfrac{63.546*10^{-3}}{2*8.3144}=114.13\,K\)
which does not show what to do next. At best at small hump around \(114.13\,K\) in a decaying conductivity profile as temperature decreases.
What about copper by itself as a metal;
\(v_{boom}=3.4354*\cfrac{8960}{29}=1061.42\,ms^{-1}\)
\(T_{boom}=1061.42^2*\cfrac{63.546*10^{-3}}{2*8.3144}=4305.29\,K\) or \(4032.14\,^oC\)
which is not indicative of its high conductivity of electricity. For this reason a folly...
\(v_{boom}=3.4354*\cfrac{6020}{56+22+8*3}=202.76\,ms^{-1}\)
\(T_{boom}=202.76^2*\cfrac{233.192*10^{-3}}{2*8.3144}=576.50\,K\) or \(303.35\,^oC\)
This is way hot. Temperature is know to decrease conductivity. An impossible hot superconductor.
For \(CaCu_3Ti_4O_{12}\),
\(v_{boom}=3.4354*\cfrac{4700}{20+29*3+22*4+8*12}=55.49\,ms^{-1}\)
\(T_{boom}=55.49^2*\cfrac{614.1789*10^{-3}}{2*8.3144}=43.17\,K\) or \(-229.98\,^oC\)
This is cold. The cell unit is too big to be considered as a quasi-nucleus. Maybe it is possible to parcel out molar mass and arrive at a density value for copper only in the crystal structure.
\(f_{Cu}=\cfrac{total\,molar\,mass\,Cu}{total\,atomic\,molar\,mass}\)
\(M_{m\,Cu}=M_m*f_{Cu}\approx molar\,mass\,Cu\)
where \(M_m\) is molecular mass,
\(\rho_{cu}=\rho_{m}.f_{cu}\)
where \(\rho_{m}\) and \(\rho_{cu}\) are crystal density and density of \(Cu\) in the structure, and so consider only copper in the structure.
So,
\(f_{Cu}=\cfrac{63.546*3}{614.1789}=0.310\)
\(\rho_{cu}=4700*0.310=1458.86\,kgm^{-3}\)
Considering only \(Cu\) in \(CaCu_3Ti_4O_{12}\),
\(v_{boom}=3.4354*\cfrac{1458.86}{29*3}=57.60\,ms^{-1}\)
\(T_{boom}=57.60^2*\cfrac{63.546*3*10^{-3}}{2*8.3144}=38.03\,K\)
It does not seem to work. Furthermore, to consider collisions with \(Cu\) only, the atomic will have to dominate the structure in size. The rest of the molecules is as if does not exist. Even so, three separate \(Cu\) atoms does not form a quasi-nucleus. Maybe,
\(v_{boom}=3.4354*\cfrac{1458.86}{29}=172.82\,ms^{-1}\)
\(T_{boom}=172.82^2*\cfrac{63.546*10^{-3}}{2*8.3144}=114.13\,K\)
What about copper by itself as a metal;
\(v_{boom}=3.4354*\cfrac{8960}{29}=1061.42\,ms^{-1}\)
\(T_{boom}=1061.42^2*\cfrac{63.546*10^{-3}}{2*8.3144}=4305.29\,K\) or \(4032.14\,^oC\)
which is not indicative of its high conductivity of electricity. For this reason a folly...
Shifting Right With High Temperature
Given,
\(v^2_{v\,p}=\cfrac{2RT_{boom}}{nM_m}\)
but
\(v^2_{boom}=\cfrac{3RT_{boom}}{nM_m}=v^2_{rms}\)
then in order for \(v_{rms}\rightarrow v_{v\,p}\) temperature has to change by,
\(T_{boom}\rightarrow \cfrac{3}{2}T_{boom}\) such that,
\(v^2_{v\,p}=\cfrac{2R}{nM_m}\cfrac{3}{2}T_{boom}=\cfrac{3RT_{boom}}{nM_m}=v^2_{boom}\)
So,
\(T_{v\,p}=\cfrac{3}{2}T_{boom}\); temperature is increased and the distribution shifted right until \(v_{p}\) is now \(v_{rms}\) previously, which was numerically, \(v_{boom}\).
It is wrong to use,
\(v^2_{boom}=\cfrac{3}{2}v^2_{p}\)
and so,
\(T_{boom}=v^2_{boom}*\cfrac{molar\,mass*10^{-3}}{3*8.3144}\)
\(T_{v\,p}=v^2_{p}*\cfrac{molar\,mass*10^{-3}}{2*8.3144}\)
\(T_{v\,p}=\cfrac{2}{3}v^2_{boom}*\cfrac{molar\,mass*10^{-3}}{2*8.3144}\)
\(T_{v\,p}=T_{boom}\)
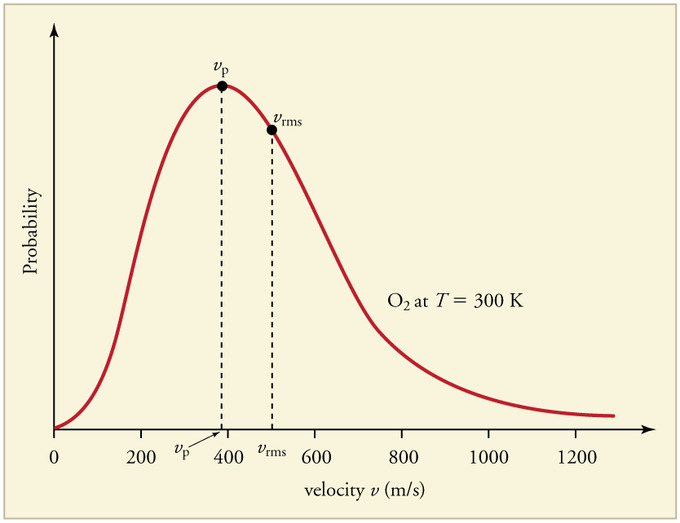
In this case,\( v_{p}\) replaces \(v_{rms}\) on the same velocity probability distribution, the temperature of the profile remains the same. \(v_{boom}\) is still at \(v_{rms}\). What is needed is to increase temperature such that \(v_{p}=v_{boom}\), on a new distribution.
Have a nice day.
\(v^2_{v\,p}=\cfrac{2RT_{boom}}{nM_m}\)
but
\(v^2_{boom}=\cfrac{3RT_{boom}}{nM_m}=v^2_{rms}\)
then in order for \(v_{rms}\rightarrow v_{v\,p}\) temperature has to change by,
\(T_{boom}\rightarrow \cfrac{3}{2}T_{boom}\) such that,
\(v^2_{v\,p}=\cfrac{2R}{nM_m}\cfrac{3}{2}T_{boom}=\cfrac{3RT_{boom}}{nM_m}=v^2_{boom}\)
So,
\(T_{v\,p}=\cfrac{3}{2}T_{boom}\); temperature is increased and the distribution shifted right until \(v_{p}\) is now \(v_{rms}\) previously, which was numerically, \(v_{boom}\).
It is wrong to use,
\(v^2_{boom}=\cfrac{3}{2}v^2_{p}\)
and so,
\(T_{boom}=v^2_{boom}*\cfrac{molar\,mass*10^{-3}}{3*8.3144}\)
\(T_{v\,p}=v^2_{p}*\cfrac{molar\,mass*10^{-3}}{2*8.3144}\)
\(T_{v\,p}=\cfrac{2}{3}v^2_{boom}*\cfrac{molar\,mass*10^{-3}}{2*8.3144}\)
\(T_{v\,p}=T_{boom}\)
In this case,\( v_{p}\) replaces \(v_{rms}\) on the same velocity probability distribution, the temperature of the profile remains the same. \(v_{boom}\) is still at \(v_{rms}\). What is needed is to increase temperature such that \(v_{p}=v_{boom}\), on a new distribution.
Have a nice day.
Radioactivity And Cold Temperature
The previous post "Half Life Calculated" dated 23 Nov 2017 suggests that temperature effects radioactivity and is maximized at one specific temperature, \( T_{v\,p}\). This temperature, however is often low in the subzero Celsius region.
Temperature is believed, does not effect radioactivity.
Maybe we are looking in the wrong direction. Cold temperature increases radioactivity and a specific temperature \(T_{v\,p}\) maximizes it.
Temperature is believed, does not effect radioactivity.
Maybe we are looking in the wrong direction. Cold temperature increases radioactivity and a specific temperature \(T_{v\,p}\) maximizes it.
Simply Scary
For \(CaGeO_3\), \(Z_m=20+32+8*3=76\) density \(3.56\,gcm^{-3}\) and molar mass \(160.7162\,gmol^{-1}\)
\(v_{boom}=3.4354*\cfrac{3560}{76}=160.92\,ms^{-1}\)
\(T_{v\,p}=160.92^2*\cfrac{160.7162*10^{-3}}{2*8.3144}=250.28\,K\) or \(-22.87\,^oC\)
which is still way low even with the use of \(v_p\) instead of \(v_{rms}\). Clearly,
\(T_{v\,p}\) or \(T_{boom}\propto density^2\) and
\(Conductivity\,at\,T_{v\,p}\gt Conductivity\,at\,T_{boom}\) due to more fraction of particles attaining \(v_{boom}\) at \( T_{v\,p}\). Conductivity is maximum at \(v_p=v_{boom}\) when \(Temperature=T_{v\,p}\).
The simple \(y=x^2\) relation of \(T_{v\,p}\) and \(T_{boom}\) with density is surprising given all the write-ups in superconductivity.
\(v_{boom}=3.4354*\cfrac{3560}{76}=160.92\,ms^{-1}\)
\(T_{v\,p}=160.92^2*\cfrac{160.7162*10^{-3}}{2*8.3144}=250.28\,K\) or \(-22.87\,^oC\)
which is still way low even with the use of \(v_p\) instead of \(v_{rms}\). Clearly,
\(T_{v\,p}\) or \(T_{boom}\propto density^2\) and
\(Conductivity\,at\,T_{v\,p}\gt Conductivity\,at\,T_{boom}\) due to more fraction of particles attaining \(v_{boom}\) at \( T_{v\,p}\). Conductivity is maximum at \(v_p=v_{boom}\) when \(Temperature=T_{v\,p}\).
The simple \(y=x^2\) relation of \(T_{v\,p}\) and \(T_{boom}\) with density is surprising given all the write-ups in superconductivity.
Most Number Of...
What if, we are to use \(v_p\) instead of \(v_{rms}\) in the discussions of perovskites solar cells and superconductors,
\(T_{v\,p}=v^2_{boom}*\cfrac{molar\,mass*10^{-3}}{2*8.3144}\)
\(T_{v\,p}=\cfrac{3}{2}T_{boom}\)
In the case of \(MgO_3Ti\) with, \(Z_m=22+12+8*3=58\) a density of \(3.36\,gcm^{-3}\) and molar mass of \(120.17\,gmol^{-1}\). Its \(T_{v\,p}\) is,
\(v_{boom}=3.4354*\cfrac{3360}{58}=199.01\)
\(T_{v\,p}=v^2_{boom}*\cfrac{molar\,mass*10^{-3}}{2*8.3144}\)
\(T_{v\,p}=\cfrac{3}{2}T_{boom}\)
In the case of \(MgO_3Ti\) with, \(Z_m=22+12+8*3=58\) a density of \(3.36\,gcm^{-3}\) and molar mass of \(120.17\,gmol^{-1}\). Its \(T_{v\,p}\) is,
\(v_{boom}=3.4354*\cfrac{3360}{58}=199.01\)
\(T_{v\,p}=199.01^2*\cfrac{120.17*10^{-3}}{2*8.3144}=286.21\,K\) or \(13.06\,^oC\)
For \(ZnTiO_3\),
\(T_{v\,p}=\cfrac{3}{2}*354.41=531.62\,K\) or \(258.46\,^ oC\)
For \(TiCaO_3\),
\(T_{v\,p}=\cfrac{3}{2}*354.41=531.62\,K\) or \(258.46\,^ oC\)
For \(TiCaO_3\),
\(350.91\,K\lt T_{v\,p}\lt402.0\,K\) or \(77.76\,^oC\lt T_{v\,p}\lt128.85\,^oC\)
For \(FeTiO_3\),
\(458.79\,K\lt T_{v\,p}\lt476.50\,K\) or \(185.64\,^oC\lt T_{v\,p}\lt203.36\,^oC\)
For \(MnTiO_3\),
\(T_{v\,p}=437.01\,K\) or \(163.83\,^oC\)
It seems that only by reducing the density of high value \(T_{v\,p}\) perozskites can \(T_{v\,p}\) at room temperature be achieved. For example a \(82.60\%\) \(MnTiO_3\) has a \(T_{v\,p}\) of
\(T_{v\,p}=0.8260^2*437.01=298.16\,K\) or \(25.01\,^oC\)
The rest of the \(100\%\), \(17.40\%\) can be with \(Fe\), \(FeTiO_3\), as long as they can form into the same crystal structure.
The rest of the \(100\%\), \(17.40\%\) can be with \(Fe\), \(FeTiO_3\), as long as they can form into the same crystal structure.
Reducing density can only reduce \(T_{v\,p}\); \(T_{v\,p}\) cannot be increased this way. Density can only be reduced given a crystalline structure.
It is likely that \(v_p\) provides the most number of freed particles that will act as charge carriers. Super-superconductor...The difference between \(v_p\) and \(v_{rms}\) is,
\(v_p=\sqrt{\cfrac{2}{3}}v_{rms}=0.667v_{rms}\)
\(v_p\) should be used instead of \(v_{rms}\); we should set \(v_{p}=\sqrt{\cfrac{2RT}{nM_m}}=v_{boom}\ne v_{rms}\) such that \(T=T_{boom}\).
And it rains again...
\(v_p=\sqrt{\cfrac{2}{3}}v_{rms}=0.667v_{rms}\)
\(v_p\) should be used instead of \(v_{rms}\); we should set \(v_{p}=\sqrt{\cfrac{2RT}{nM_m}}=v_{boom}\ne v_{rms}\) such that \(T=T_{boom}\).
And it rains again...
Thursday, November 23, 2017
Half Life Calculated
Given \(T\),
The probability of any particle attaining \(v_{boom}\) is \(p_v\). If radioactive decay is the result of particles colliding at \(v_{boom}\), then the portion of particles decaying away at any one time is,
\(\cfrac{dN}{dt}=-p_v.N\) --- (*)
where \(N\) is the number of particles.
\(N(t)=N_oe^{-p_vt}\)
where \(N_o\) is the number of particles at time \(t=0\). Consider,
\(\cfrac{1}{2}N_o=N_oe^{-p_vt_{1/2}}\)
\(t_{1/2}=\cfrac{ln(2)}{p_v}\)
Half life can be calculated from a graph of Probability, \(p\) vs Velocity, \(v\). Unfortunately such plots are often illustrative. The velocities profile of free particles in a solid has never been done.
Note: Expression (*) requires that \(p_v=\cfrac{N_v}{N}\) where \(N_v\) is the number of particles with velocity equals to \(v_{boom}\) and \(N\) is the total number of particles; that the probability of a particle having \(v_{boom}\) is the fraction of particles having \(v_{boom}\).
The probability of any particle attaining \(v_{boom}\) is \(p_v\). If radioactive decay is the result of particles colliding at \(v_{boom}\), then the portion of particles decaying away at any one time is,
\(\cfrac{dN}{dt}=-p_v.N\) --- (*)
where \(N\) is the number of particles.
\(N(t)=N_oe^{-p_vt}\)
where \(N_o\) is the number of particles at time \(t=0\). Consider,
\(\cfrac{1}{2}N_o=N_oe^{-p_vt_{1/2}}\)
\(t_{1/2}=\cfrac{ln(2)}{p_v}\)
Half life can be calculated from a graph of Probability, \(p\) vs Velocity, \(v\). Unfortunately such plots are often illustrative. The velocities profile of free particles in a solid has never been done.
Note: Expression (*) requires that \(p_v=\cfrac{N_v}{N}\) where \(N_v\) is the number of particles with velocity equals to \(v_{boom}\) and \(N\) is the total number of particles; that the probability of a particle having \(v_{boom}\) is the fraction of particles having \(v_{boom}\).
Tuning Down \(T_{boom}\)
With \(ZnTiO_3\), with \(Z_m=30+22+8*3=76\), molar mass of \(161.24\,gmol^{-1}\) and a density of \(5.18\,gcm^{-3}\),
\(v_{boom}=3.4354*\cfrac{5180}{76}=234.14\,ms^{-1}\)
and
\(T_{boom}=234.14^2*\cfrac{161.24*10^{-3}}{3*8.3144}=354.41\,K\) or \(81.26\,^oC\)
If \(ZnTiO_3\) crystal are reduced in density to 91.72% by adding a dopant (\(Mn\), \(Fe\) are all capable of oxidation state \(+3\)), then \(T_{boom}\) is reduced by,
\(T_{boom}=0.9172^2*354.41=298.15\,K\) or \(25.00\,^oC\)
Changing the crystal's density tunes down \(T_{boom}\). Goodnight.
\(v_{boom}=3.4354*\cfrac{5180}{76}=234.14\,ms^{-1}\)
and
\(T_{boom}=234.14^2*\cfrac{161.24*10^{-3}}{3*8.3144}=354.41\,K\) or \(81.26\,^oC\)
If \(ZnTiO_3\) crystal are reduced in density to 91.72% by adding a dopant (\(Mn\), \(Fe\) are all capable of oxidation state \(+3\)), then \(T_{boom}\) is reduced by,
\(T_{boom}=0.9172^2*354.41=298.15\,K\) or \(25.00\,^oC\)
Changing the crystal's density tunes down \(T_{boom}\). Goodnight.
Pyrophanite Is Eighteen
Pyrophanite, \(MnTiO_3\) of \(Z_m=25+22+8*3=71\), a specific gravity of \(4.537\) and a molar mass of \(150.8032\,gmol^{-1}\),
\(v_{boom}=3.4354*\cfrac{4537}{71}=219.52\,ms^{-1}\)
and a \(T_{boom}\) range of,
\(T_{boom}=219.52^2*\cfrac{150.8032*10^{-3}}{3*8.3144}=291.34\,K\) or \(18.19\,^oC\)
This temperature, some might consider room temperature, but under the sun I would prefer, Ilmenite at \(32.71\,^oC\)
Remember only specifically at \(T_{boom}\). Even if Pyrophanite cannot act as a solar cell it can be a charge cell where charging occurs at \(T_{boom}\) quickly followed by a slow discharge at off \(T_{boom}\) temperature.
Have a sunny day.
This temperature, some might consider room temperature, but under the sun I would prefer, Ilmenite at \(32.71\,^oC\)
Remember only specifically at \(T_{boom}\). Even if Pyrophanite cannot act as a solar cell it can be a charge cell where charging occurs at \(T_{boom}\) quickly followed by a slow discharge at off \(T_{boom}\) temperature.
Have a sunny day.
Wednesday, November 22, 2017
Perovskite Crystal And Critical Temperature
Perovskite crystal has a repeating unit of \(TiCaO_3\), \(Z_m=22+20+8*3=66\) and a formula mass of \(135.96\,gmol^{-1}\) and a specific gravity of \(3.98–4.26\).
\(v_{boom}=3.4354*\cfrac{3980}{66}=207.17\)
\(v_{boom}=3.4354*\cfrac{4260}{66}=221.74\)
A \(v_{boom}\) range of \(207.17\) to \(221.74\).
And a corresponding \(T_{boom}\) range of,
\(T_{boom}=207.17^2*\cfrac{135.96*10^{-3}}{3*8.3144}=233.94\,K\)
\(T_{boom}=221.74^2*\cfrac{135.96*10^{-3}}{3*8.3144}=268.0\,K\)
\(233.94\,K\lt T_{boom}\lt268.0\,K\)
which is about \(-5.14\,^oC\) to \(-39.20\,^oC\)
A very cold solar cell.
If we replace \(Ca\) with \(Mg\), \(MgO_3Ti\) with, \(Z_m=22+12+8*3=58\) a density of \(3.36\,gcm^{-3}\) and molar mass of \(120.17\,gmol^{-1}\). Its \(T_{boom}\) is,
\(v_{boom}=3.4354*\cfrac{3360}{58}=199.01\)
\(v_{boom}=3.4354*\cfrac{3980}{66}=207.17\)
\(v_{boom}=3.4354*\cfrac{4260}{66}=221.74\)
A \(v_{boom}\) range of \(207.17\) to \(221.74\).
And a corresponding \(T_{boom}\) range of,
\(T_{boom}=207.17^2*\cfrac{135.96*10^{-3}}{3*8.3144}=233.94\,K\)
\(T_{boom}=221.74^2*\cfrac{135.96*10^{-3}}{3*8.3144}=268.0\,K\)
\(233.94\,K\lt T_{boom}\lt268.0\,K\)
which is about \(-5.14\,^oC\) to \(-39.20\,^oC\)
A very cold solar cell.
If we replace \(Ca\) with \(Mg\), \(MgO_3Ti\) with, \(Z_m=22+12+8*3=58\) a density of \(3.36\,gcm^{-3}\) and molar mass of \(120.17\,gmol^{-1}\). Its \(T_{boom}\) is,
\(v_{boom}=3.4354*\cfrac{3360}{58}=199.01\)
with a lower molar mass this is going to lower \(T_{boom}\) further.
And \(TiBeO_3\) does not seems to exist, but the search leads to Ilmenite, \(FeTiO_3\) of \(Z_m=26+22+8*3=72\), a specific gravity of \(4.70–4.79\) and a molar mass of \(151.7102\,gmol^{-1}\),
\(v_{boom}=3.4354*\cfrac{4700}{72}=224.25\)
\(v_{boom}=3.4354*\cfrac{4790}{72}=228.54\)
and a \(T_{boom}\) range of,
\(T_{boom}=228.54^2*\cfrac{151.7102*10^{-3}}{3*8.3144}=317.67\,K\)
\(T_{boom}=224.25^2*\cfrac{151.7102*10^{-3}}{3*8.3144}=305.86\,K\)
and it is over the range of \(32.71\,^oC\) to \(44.53\,^oC\). We may have a winner with Ilmenite as a room temperature superconductor!
Conductivity, Critical Temperature
Particles that shed from a nucleus or quasi nucleus as the result of collisions at \(v_{boom}\) are basic particles of all nature. The equation,
\(v_{boom}=3.4354*\cfrac{density}{particle\,count\,per\,type}\)
considers the count of particles of each and all types in the nucleus or quasi nucleus. These are basic particle that are a quarter of the normal charge. (post "New Discrepancies And Hollow Earth" dated 23 Jun2016)
In matter that are conductive of a specific type of particles, negative charges in conductors, negative gravity particles in crystal and temperature particles in thermal conductors, these freed charges increases conductivity. This occurs at a specific temperature \(T_{boom}\),
\(T_{v\,boom}=v^2_{boom}*\cfrac{molar\,mass*10^{-3}}{3*8.3144}\)
Have a nice day.
\(v_{boom}=3.4354*\cfrac{density}{particle\,count\,per\,type}\)
considers the count of particles of each and all types in the nucleus or quasi nucleus. These are basic particle that are a quarter of the normal charge. (post "New Discrepancies And Hollow Earth" dated 23 Jun2016)
In matter that are conductive of a specific type of particles, negative charges in conductors, negative gravity particles in crystal and temperature particles in thermal conductors, these freed charges increases conductivity. This occurs at a specific temperature \(T_{boom}\),
\(T_{v\,boom}=v^2_{boom}*\cfrac{molar\,mass*10^{-3}}{3*8.3144}\)
Have a nice day.
Fuss With Time
Why is the \(x\) axis in the post "Thought Experiment Gone Wrong" dated 19 Nov 2017 moving at one unit per unit time?
Because the origin is defined as a point. A line is a point moving. In this case arbitrarily at one unit per unit time and the axis goes on forever. A short line is a point moved, given its velocity, \(v\)
\(L=\int^{t}_0{v}dt=\sqrt{\left(\int^{t}_{0}{v(x,\,t)}dt\right)^2+\left(\int^{t}_{0}{v(y,\,t)}dt\right)^2}\)
where \(v(y,\,t)\) is the \(y\) component of \(v\) and \(v(x,\,t)\) is the \(x\) component of \(v\). \(v\) is a vector integrated over time. With,
\(\cfrac{d y}{d t}=a\)
\(\cfrac{d x}{d t}=b\)
and so,
\(\cfrac{d y}{d x}=\cfrac{a}{b}\)
with
\((x_1,\,y_1)\) as the starting point,
\(L=\sqrt{\left(\int^{x_2}_{x_1}{v(x,\,t)\cfrac{1}{b}}dx\right)^2+\left(\int^{y_2}_{y_1}{v(y,\,t)\cfrac{1}{a}}dy\right)^2}\)
Because the origin is defined as a point. A line is a point moving. In this case arbitrarily at one unit per unit time and the axis goes on forever. A short line is a point moved, given its velocity, \(v\)
\(L=\int^{t}_0{v}dt=\sqrt{\left(\int^{t}_{0}{v(x,\,t)}dt\right)^2+\left(\int^{t}_{0}{v(y,\,t)}dt\right)^2}\)
where \(v(y,\,t)\) is the \(y\) component of \(v\) and \(v(x,\,t)\) is the \(x\) component of \(v\). \(v\) is a vector integrated over time. With,
\(\cfrac{d y}{d t}=a\)
\(\cfrac{d x}{d t}=b\)
and so,
\(\cfrac{d y}{d x}=\cfrac{a}{b}\)
with
\((x_1,\,y_1)\) as the starting point,
\(L=\sqrt{\left(\int^{x_2}_{x_1}{v(x,\,t)\cfrac{1}{b}}dx\right)^2+\left(\int^{y_2}_{y_1}{v(y,\,t)\cfrac{1}{a}}dy\right)^2}\)
\((x_2,\,y_2)\) is the end point after time \(t\), and \(y_2=\cfrac{a}{b}(x_2-x_1)+y_1\) and
\(x_1=b.t\)
Over one unit time,
\(x_2=b + x_1\)
and
\(y_2=a + y_1\)
but,
\(v(y,\,t)=\cfrac{d y}{d t}=a\)
\(v(x,\,t)=\cfrac{d x}{d t}=b\)
so,
\(L=\sqrt{\left(\int^{x_2}_{x_1}{b\cfrac{1}{b}}dx\right)^2+\left(\int^{y_2}_{y_1}{a\cfrac{1}{a}}dy\right)^2}\)
\(L=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt{b^2+a^2}\)
which is what is expected. Why the fuss? We started with the origin as a point, the rest of the graph is with this point as the lowest denominator. A infinite line is a point with a velocity; a finite length on the graph is a point with a velocity after a finite integral over an arbitrary time interval.
Both length and the axes have a direction and are vectors. A curve is a point with changing velocity. Intersections are paths that crosses irrespective of time. But a collision is in both space and time.
Still what's the fuss? The time dimension enters into the discussion because the issue at hand is space and time in spacetime diagrams.
Tuesday, November 21, 2017
All You Have To Do Is WAIT
As \(v\rightarrow c\)
\(\left.\begin{array}{l}t=\cfrac{v}{c}x\\t=\cfrac{c}{v}x\end{array}\right\rbrace\rightarrow t=x\)
could be the reason why people think that if we travel at light speed we also travel through time. Or that time is at light speed, \(c\).
The last is true, only if light speed is the speed limit. Light speed is set as the speed limit when the scaling factor \(c\) was applied to Lorentz transform that scaled,
\(v\lt1\) to \(v\lt c\)
As for time travel (in the time dimension) at light speed in the space dimension...You cannot travel in the orthogonal direction \(y\) even if you are at light speed in the direction \(x\). Space and time are orthogonal dimensions. However, in a gravitational field, a change in gravity that changes your time speed that incidentally also propels you to light speed and back, may move you back and forth in time with respect to the rest of us. We are all traveling at the same time speed, already.
We are already traveling through time. To go forward by ten years. all you have to do is WAIT.
Note: Time, time speed and light speed are different things. \(Time\,speed\,=\,light\,speed\) is an assumption.
\(\left.\begin{array}{l}t=\cfrac{v}{c}x\\t=\cfrac{c}{v}x\end{array}\right\rbrace\rightarrow t=x\)
could be the reason why people think that if we travel at light speed we also travel through time. Or that time is at light speed, \(c\).
The last is true, only if light speed is the speed limit. Light speed is set as the speed limit when the scaling factor \(c\) was applied to Lorentz transform that scaled,
\(v\lt1\) to \(v\lt c\)
As for time travel (in the time dimension) at light speed in the space dimension...You cannot travel in the orthogonal direction \(y\) even if you are at light speed in the direction \(x\). Space and time are orthogonal dimensions. However, in a gravitational field, a change in gravity that changes your time speed that incidentally also propels you to light speed and back, may move you back and forth in time with respect to the rest of us. We are all traveling at the same time speed, already.
We are already traveling through time. To go forward by ten years. all you have to do is WAIT.
Note: Time, time speed and light speed are different things. \(Time\,speed\,=\,light\,speed\) is an assumption.
Time, Time Speed And Gravity
When the argument in the previous post "Who Has A Longer Penis?" dated 21 Nov 2017 is applied to time duration, then to a travelling observer at high speed, any movements on an object at rest is in slow motion; to a observer at rest, any movements on a travelling object is quicken up.
That does not mean that the travelling object age faster. One second at rest, is longer while travelling when measured by the observer at rest. It is the same one second as experienced by the traveler. Both the traveler and rest observed experience the same time speed.
Gravity changes time speed. Free motion under the effect of a gravitational field, changes time speed.
A travelling person on the surface of earth age the same as when the person is at rest, even if it is at light speed, because gravity is the same and so their time speed is the same. (post "Time, Time Speed, Aging" dated 24 Apr 2014). GPS time is adjusted because of the difference in gravity the satellite experiences, which is related to its orbital speed because of its circular motion around earth. GPS experiences a different time speed not directly because of its orbital speed.
Under the action of a gravitational field without propulsion, acceleration to light speed means time stand still.
But the scaling factor \(c\) is arbitrary. Lorentz transform does not proof the light speed limit but applies the light speed limit, \(c\).
Have a nice day.
Who Has A Longer Penis?
Relatively speaking, no matter who you are,
\(OP\gt OQ\)
and as
\(v\rightarrow c\)
\(\left.\begin{array}{l}t=\cfrac{v}{c}x\\t=\cfrac{c}{v}x\end{array}\right\rbrace\rightarrow t=x\)
which is why the graph is better shown with \(v\rightarrow \cfrac{v}{c}\).
Who has a longer penis? You, or you traveling at speed \(v\)? It matters only if you are facing in the \(v\) direction. In the direction perpendicular to \(v\), you are equally disadvantaged. And it matters who is measuring, you or an observer at rest.
The traveling length \(OP\) as measured by a rest frame becomes \(OQ\). To an observer at rest, a length \(OP\) traveling at \(v\), lengthwise, is contracted to \(OQ\). A fast travelling space ship appears shorter, as it zooms past.
And to a travelling observer, a length at rest \(OQ\) is measured to be longer, of length \(OP\). To the spaceship as it zoom away at high speed, everything stationary, elongates. And a point of star becomes a line.
\(O\), \(P\) and \(Q\) are simultaneous points.
Your penis, travelling with you is still the same wienie length to you, no matter how you measured it.
Have a nice day.
\(OP\gt OQ\)
and as
\(v\rightarrow c\)
\(\left.\begin{array}{l}t=\cfrac{v}{c}x\\t=\cfrac{c}{v}x\end{array}\right\rbrace\rightarrow t=x\)
which is why the graph is better shown with \(v\rightarrow \cfrac{v}{c}\).
Who has a longer penis? You, or you traveling at speed \(v\)? It matters only if you are facing in the \(v\) direction. In the direction perpendicular to \(v\), you are equally disadvantaged. And it matters who is measuring, you or an observer at rest.
The traveling length \(OP\) as measured by a rest frame becomes \(OQ\). To an observer at rest, a length \(OP\) traveling at \(v\), lengthwise, is contracted to \(OQ\). A fast travelling space ship appears shorter, as it zooms past.
And to a travelling observer, a length at rest \(OQ\) is measured to be longer, of length \(OP\). To the spaceship as it zoom away at high speed, everything stationary, elongates. And a point of star becomes a line.
\(O\), \(P\) and \(Q\) are simultaneous points.
Your penis, travelling with you is still the same wienie length to you, no matter how you measured it.
Have a nice day.
Monday, November 20, 2017
Of Course Uranium-235
Why is Uranium-235 explosive?
\(v_{boom}=3.4354*\cfrac{19100}{92}=713.22\,ms^{-1}\)
Given sonic boom at \(v_{sonic}=342.53\,ms^{-1}\) from the post "Sonic Boom Updated" dated 30 Oct 2017.
\(\cfrac{v_{boom}}{v_{sonic}}=\cfrac{713.22}{342.53}=2.08\)
After the detonation, the explosive front moves off at sonic boom speed that is twice less than \(v_{boom}\) of Uranium-235, two head on collisions at \(342.53\,ms^{-1}\) can generate enough \(KE\) (\(2\times342.53\,ms^{-1}\)) and trigger nuclear disintegration of the Uranium. A-bomb is destructive because of this moving nuclear front at sonic boom speed. Otherwise a bomb is destructive after the release of heat and pressure built up just after detonation. The material does no continue to disintegrate as it is thrown from the explosion. The built up of heat and pressure is limited by the bomb's containment. Any weakness in the containment will reduce its destructiveness. The destructiveness of an A-bomb on the other hand, depends on it attaining \(v_{boom}\) that is half of the sonic boom. Prevent \(v_{boom}\) and the A-bomb is no more dangerous than boiling iron at \(3635.16\,K\). If the A-bomb is further contained and the nuclear material is prevented from attaining \(v_{boom}\), its destructiveness will be reduced.
Maybe... and thankfully \(^{235}U\) is difficult to obtain.
Which might lead us to water with \(v_{boom}=v_{sonic}\). A sonic boom is totally destructive, very loud (ie high pressure) and very hot, but not radioactive thereafter and not usually sustained.
Tabooo....
\(v_{boom}=3.4354*\cfrac{19100}{92}=713.22\,ms^{-1}\)
Given sonic boom at \(v_{sonic}=342.53\,ms^{-1}\) from the post "Sonic Boom Updated" dated 30 Oct 2017.
\(\cfrac{v_{boom}}{v_{sonic}}=\cfrac{713.22}{342.53}=2.08\)
After the detonation, the explosive front moves off at sonic boom speed that is twice less than \(v_{boom}\) of Uranium-235, two head on collisions at \(342.53\,ms^{-1}\) can generate enough \(KE\) (\(2\times342.53\,ms^{-1}\)) and trigger nuclear disintegration of the Uranium. A-bomb is destructive because of this moving nuclear front at sonic boom speed. Otherwise a bomb is destructive after the release of heat and pressure built up just after detonation. The material does no continue to disintegrate as it is thrown from the explosion. The built up of heat and pressure is limited by the bomb's containment. Any weakness in the containment will reduce its destructiveness. The destructiveness of an A-bomb on the other hand, depends on it attaining \(v_{boom}\) that is half of the sonic boom. Prevent \(v_{boom}\) and the A-bomb is no more dangerous than boiling iron at \(3635.16\,K\). If the A-bomb is further contained and the nuclear material is prevented from attaining \(v_{boom}\), its destructiveness will be reduced.
Maybe... and thankfully \(^{235}U\) is difficult to obtain.
Which might lead us to water with \(v_{boom}=v_{sonic}\). A sonic boom is totally destructive, very loud (ie high pressure) and very hot, but not radioactive thereafter and not usually sustained.
Tabooo....
Sunday, November 19, 2017
When Right Angle Is Not
Given,
\(x^{'}=\cfrac{x-vt}{\sqrt{1-v^2}}\)
what happens when \(v\ge1\)?
When \(x^{'}\) was set to \(1\) in the triangle (post "Thought Experiment Gone Wrong" dated 20 Nov 2017),
\(cos(\theta)=\cfrac{\sqrt{1-v^2}}{1}\)
we are attempting to transform \(x^{'}\) to \(x\) where it is calibrated to unit length. We are saying if \(x^{'}\) is to be one unit what do we need to do to \(x\). Using the triangle restricts the value of \(v\) to less than \(1\).
So, given \(v\) and \(x\) and \(v\ge 1\) to use the transform, both \(v\) and \(x\) are scale up to the value of the highest speed possible, light speed \(c\) and \(|c|\) respectively;
\(\cfrac{v}{c}\rightarrow v\)
\(\cfrac{x}{|c|}\rightarrow x\)
and \(x^{'}\) is also measured in the unit of \(c\) per unit time.
\(\cfrac{x^{'}}{|c|}\rightarrow x^{'}\)
And hence Lorentz's transform.
Note: If \(x=10\,m\) then to used Lorentz transform we need \(\cfrac{10}{299792458}\rightarrow x\) instead of just \(x=10\).
\(x^{'}=\cfrac{x-vt}{\sqrt{1-v^2}}\)
what happens when \(v\ge1\)?
When \(x^{'}\) was set to \(1\) in the triangle (post "Thought Experiment Gone Wrong" dated 20 Nov 2017),
\(cos(\theta)=\cfrac{\sqrt{1-v^2}}{1}\)
we are attempting to transform \(x^{'}\) to \(x\) where it is calibrated to unit length. We are saying if \(x^{'}\) is to be one unit what do we need to do to \(x\). Using the triangle restricts the value of \(v\) to less than \(1\).
So, given \(v\) and \(x\) and \(v\ge 1\) to use the transform, both \(v\) and \(x\) are scale up to the value of the highest speed possible, light speed \(c\) and \(|c|\) respectively;
\(\cfrac{v}{c}\rightarrow v\)
\(\cfrac{x}{|c|}\rightarrow x\)
and \(x^{'}\) is also measured in the unit of \(c\) per unit time.
\(\cfrac{x^{'}}{|c|}\rightarrow x^{'}\)
And hence Lorentz's transform.
Note: If \(x=10\,m\) then to used Lorentz transform we need \(\cfrac{10}{299792458}\rightarrow x\) instead of just \(x=10\).
Adjusting For Unit Consistency, Lorentz's
With reference to the previous post, "Thought Experiment Gone Wrong" dated 20 Nov 2017, when we replace "units" with meters and uses light speed, \(c\) as standard,
Instead of one unit,
\(x^{'}cos(\theta)=x^{'}.\cfrac{\sqrt{c^2-v^2}}{c}=x^{'}.\sqrt{1-\cfrac{v^2}{c^2}}=x\)
So,
\(x^{'}=\cfrac{x}{\sqrt{1-\cfrac{v^2}{c^2}}}\) --- (*)
as the origin is still displaced by \(vt\),
\(x^{'}=x-vt\)
but the dilation needed is now given by (*), so,
\(x^{'}=\cfrac{x-vt}{\sqrt{1-\cfrac{v^2}{c^2}}}\)
and the rest of Lorentz transformations follows.
What does it mean when we use light speed this way? \(c\), instead of one unit? It means, \(v\) is in units of 299792458 ms-1 and \(x\) in units of 299792458 m. But it is OK because,
\(c.x^{'}=\cfrac{c.x-c.vt}{\sqrt{1-\cfrac{(c.v)^2}{c^2}}}\)
where \(x^{' }\), \(x\) and \(v\) are in units or unit meter and unit meter per unit time, respectively.
\(c.x^{'}=c.\cfrac{x-vt}{\sqrt{1-v^2}}\)
\(x^{'}=\cfrac{x-vt}{\sqrt{1-v^2}}\)
which is the same as before. But! when \(\gamma=\cfrac{1}{\sqrt{1-\cfrac{v^2}{c^2}}}\),
\(\cfrac{x}{|c|}\rightarrow x\)
\(\cfrac{x^{'}}{|c|}\rightarrow x^{'}\)
and
\(\cfrac{v}{c}\rightarrow v\)
we are using light speed as reference, everything is measured in 299792458 m or 299792458 ms-1.
Have a nice day.
Instead of one unit,
\(x^{'}cos(\theta)=x^{'}.\cfrac{\sqrt{c^2-v^2}}{c}=x^{'}.\sqrt{1-\cfrac{v^2}{c^2}}=x\)
So,
\(x^{'}=\cfrac{x}{\sqrt{1-\cfrac{v^2}{c^2}}}\) --- (*)
as the origin is still displaced by \(vt\),
\(x^{'}=x-vt\)
but the dilation needed is now given by (*), so,
\(x^{'}=\cfrac{x-vt}{\sqrt{1-\cfrac{v^2}{c^2}}}\)
and the rest of Lorentz transformations follows.
What does it mean when we use light speed this way? \(c\), instead of one unit? It means, \(v\) is in units of 299792458 ms-1 and \(x\) in units of 299792458 m. But it is OK because,
\(c.x^{'}=\cfrac{c.x-c.vt}{\sqrt{1-\cfrac{(c.v)^2}{c^2}}}\)
where \(x^{' }\), \(x\) and \(v\) are in units or unit meter and unit meter per unit time, respectively.
\(c.x^{'}=c.\cfrac{x-vt}{\sqrt{1-v^2}}\)
\(x^{'}=\cfrac{x-vt}{\sqrt{1-v^2}}\)
which is the same as before. But! when \(\gamma=\cfrac{1}{\sqrt{1-\cfrac{v^2}{c^2}}}\),
\(\cfrac{x}{|c|}\rightarrow x\)
\(\cfrac{x^{'}}{|c|}\rightarrow x^{'}\)
and
\(\cfrac{v}{c}\rightarrow v\)
we are using light speed as reference, everything is measured in 299792458 m or 299792458 ms-1.
Have a nice day.
Thought Experiment Gone Wrong
I was reading...
where clock \(C\) is exactly between clock \(A\) and Clock \(B\) and at noon both clocks flash in the directions of \(C\). If \(A\) and \(B\) are synchronized, then \(C\) receives both flashes of light simultaneously. A forth observer travelling to the right with velocity \(v\), will not receive the pulse simultaneously and the argument leads to Lorentz transform.
If our focus is on the clock being EXACTLY synchronized, then the directions of the light flashes are SPECIFICALLY in the \(C\) directions. \(X\) in the first place, does not first receive a pulse from clock \(B\) and then a pulse from clock \(A\). \(X\), while traveling misses both pulses aimed at \(C\). \(X\) travelling at velocity \(v\), do not see the light AT ALL. Neither does the position \(x\), where the moving clock \(X\) is instantaneously at, in space, while traveling at velocity, \(v\), at noon, receive any light pulse from \(A\) and \(B\).
If \(X\) happens to be at \(C\) at noon, it will not receive any pulses as it passes \(C\) because the pulses arrive after \(X\) has passed by. If \(X\) happens to be at \(C\), a little after noon, when the pulses arrive, \(X\) will receive both pulses. It cannot receive one pulse after another and conclude that the clocks \(A\) and \(B\) are not synchronized. \(X\) receives both pulses or none, and can only affirms that the clocks are synchronized and but cannot deduce that the clocks are not synchronized.
If X does receive a pulse, it is one aimed specifically at it and is necessarily of a different path length; ray \(a\ne b\), unless \(X\) is at \(C\) when the pulses arrive.
If we are to specify time exactly then light as a vector, its direction must also be specified exactly.
Otherwise, we rely on the conservation of energy, that in all frames of reference, the total energy contained within those frames, in the system, is the same.
where a frame with a moving origin at velocity, \(v\) and an \(x\) axis moving at one unit per unit time with respect to the origin is transformed back to a frame with a stationary origin and an \(x\) axis moving at one unit per unit time. Yes, the \(x\) axis is moving at one unit per unit time with respect to the origin. And the origin, a point, is orthogonal to all axes. The origin of the moving frame moving at \(v\),
\(x^{'}=x-vt\)
at the same time, one unit along \(x^{'}\) is actually longer than one unit along \(x\) in the rest frame,
\(x^{'}cos(\theta)=x^{'}.\cfrac{\sqrt{1-v^2}}{1}=x\)
So, in the rest frame units along \(x\),
\(x^{'}=\cfrac{x}{\sqrt{1-v^2}}\)
thus,
\(x^{'}=\cfrac{x-vt}{\sqrt{1-v^2}}\)
we move the origin in time by \(vt\) and scaled the units along \(x\) axis by \(\cfrac{1}{\sqrt{1-v^2}}\) to obtain the equivalent of a moving frame with respect to the rest frame.
And the rest of Lorentz transform between rest frame and moving frames follows. It is conservation of energy because we are dealing with velocity squared terms.
where clock \(C\) is exactly between clock \(A\) and Clock \(B\) and at noon both clocks flash in the directions of \(C\). If \(A\) and \(B\) are synchronized, then \(C\) receives both flashes of light simultaneously. A forth observer travelling to the right with velocity \(v\), will not receive the pulse simultaneously and the argument leads to Lorentz transform.
If our focus is on the clock being EXACTLY synchronized, then the directions of the light flashes are SPECIFICALLY in the \(C\) directions. \(X\) in the first place, does not first receive a pulse from clock \(B\) and then a pulse from clock \(A\). \(X\), while traveling misses both pulses aimed at \(C\). \(X\) travelling at velocity \(v\), do not see the light AT ALL. Neither does the position \(x\), where the moving clock \(X\) is instantaneously at, in space, while traveling at velocity, \(v\), at noon, receive any light pulse from \(A\) and \(B\).
If \(X\) happens to be at \(C\) at noon, it will not receive any pulses as it passes \(C\) because the pulses arrive after \(X\) has passed by. If \(X\) happens to be at \(C\), a little after noon, when the pulses arrive, \(X\) will receive both pulses. It cannot receive one pulse after another and conclude that the clocks \(A\) and \(B\) are not synchronized. \(X\) receives both pulses or none, and can only affirms that the clocks are synchronized and but cannot deduce that the clocks are not synchronized.
If X does receive a pulse, it is one aimed specifically at it and is necessarily of a different path length; ray \(a\ne b\), unless \(X\) is at \(C\) when the pulses arrive.
If we are to specify time exactly then light as a vector, its direction must also be specified exactly.
Otherwise, we rely on the conservation of energy, that in all frames of reference, the total energy contained within those frames, in the system, is the same.
where a frame with a moving origin at velocity, \(v\) and an \(x\) axis moving at one unit per unit time with respect to the origin is transformed back to a frame with a stationary origin and an \(x\) axis moving at one unit per unit time. Yes, the \(x\) axis is moving at one unit per unit time with respect to the origin. And the origin, a point, is orthogonal to all axes. The origin of the moving frame moving at \(v\),
\(x^{'}=x-vt\)
at the same time, one unit along \(x^{'}\) is actually longer than one unit along \(x\) in the rest frame,
\(x^{'}cos(\theta)=x^{'}.\cfrac{\sqrt{1-v^2}}{1}=x\)
So, in the rest frame units along \(x\),
\(x^{'}=\cfrac{x}{\sqrt{1-v^2}}\)
thus,
\(x^{'}=\cfrac{x-vt}{\sqrt{1-v^2}}\)
we move the origin in time by \(vt\) and scaled the units along \(x\) axis by \(\cfrac{1}{\sqrt{1-v^2}}\) to obtain the equivalent of a moving frame with respect to the rest frame.
And the rest of Lorentz transform between rest frame and moving frames follows. It is conservation of energy because we are dealing with velocity squared terms.
Crystal Liquid
Can a crystal be liquefied? Possibly with \(p^{+}\). Does crystal softens in \(H_2\) gas? The lattice bonds in common solids are of charge particles that are weaken by the presence of \(T^{+}\) particles. In orbital motion the \(T^{+}\) particles produce weak electric fields. So, crystals held together by gravity particles are weaken by \(p^{+}\) particles that, in orbits, produce weak gravitational fields.
If crystals are so effected by gravity then, gravity can be measured by the change in Young's modulus of a crystal under gravity, along gravity's line of action. A change in Young's modulus changes the length of the crystal that if set into oscillations changes its frequency.
If crystals are so effected by gravity then, gravity can be measured by the change in Young's modulus of a crystal under gravity, along gravity's line of action. A change in Young's modulus changes the length of the crystal that if set into oscillations changes its frequency.
Does glass flow and deform quicker in hydrogen gas?
It's Complicated
To admit basic particles that are free in a solids, we have to look at the expression,
\(v_{boom}=3.4354*\cfrac{density}{particle\,count\,per\,type}\)
again.
\(Z=1\) for basic particles.
In case of basic particles alone,
\(v_{boom\,particles}=3.4354*{density}\) - (1)
where \(density\) is the particle density within the confined volume in a solid or a gas containment.
In the case of basic particles colliding with the lattice cells,
\(v_{boom}=3.4354*\cfrac{density}{(Z=1)*(particle\,count\,per\,type)}\) -- (2)
which the same as before.
In the case of a gas,
\(v_{boom}=3.4354*\cfrac{density}{(particle\,count\,per\,type)*(particle\,count\,per\,type)}\) --- (3)
where molecules collide. Particle count per type is the total number of particles of one type that constitute the molecule.
In a solid and liquid we have the superposition of (1) and (2). In a gas we have the superposition of (1), (2) and (3). We might add, in the case of basic particles colliding with matter in the liquid state,
\(v_{boom}=3.4354*\cfrac{density}{(Z=1)*m*(particle\,count\,per\,type)}\) -- (4)
where \(m\) is the average number of molecules in a cluster/chain in the liquid state.
If these other scenario occurs, then the plot of energy states given temperature will be the superposition of two or more graphs as enumerated above. Each change in phase (solid\(\rightarrow \)liquid, liquid\(\rightarrow \)gas) introduces a new superimposed graph.
As an after thought, we might also add, collisions between molecule clusters in a gas,
\(v_{boom}=3.4354*\cfrac{density}{m*(particle\,count\,per\,type)*m*(particle\,count\,per\,type)}\) --- (5)
where \(m\) is the average molecular cluster size in the gas. And
\(v_{boom}=3.4354*\cfrac{density}{m*(particle\,count\,per\,type)*(particle\,count\,per\,type)}\) --- (6)
for collisions between molecule clusters and singular molecule in a gas
And things get complicated, with many shadows.
\(v_{boom}=3.4354*\cfrac{density}{particle\,count\,per\,type}\)
again.
\(Z=1\) for basic particles.
In case of basic particles alone,
\(v_{boom\,particles}=3.4354*{density}\) - (1)
where \(density\) is the particle density within the confined volume in a solid or a gas containment.
In the case of basic particles colliding with the lattice cells,
\(v_{boom}=3.4354*\cfrac{density}{(Z=1)*(particle\,count\,per\,type)}\) -- (2)
which the same as before.
In the case of a gas,
\(v_{boom}=3.4354*\cfrac{density}{(particle\,count\,per\,type)*(particle\,count\,per\,type)}\) --- (3)
where molecules collide. Particle count per type is the total number of particles of one type that constitute the molecule.
In a solid and liquid we have the superposition of (1) and (2). In a gas we have the superposition of (1), (2) and (3). We might add, in the case of basic particles colliding with matter in the liquid state,
\(v_{boom}=3.4354*\cfrac{density}{(Z=1)*m*(particle\,count\,per\,type)}\) -- (4)
where \(m\) is the average number of molecules in a cluster/chain in the liquid state.
If these other scenario occurs, then the plot of energy states given temperature will be the superposition of two or more graphs as enumerated above. Each change in phase (solid\(\rightarrow \)liquid, liquid\(\rightarrow \)gas) introduces a new superimposed graph.
As an after thought, we might also add, collisions between molecule clusters in a gas,
\(v_{boom}=3.4354*\cfrac{density}{m*(particle\,count\,per\,type)*m*(particle\,count\,per\,type)}\) --- (5)
where \(m\) is the average molecular cluster size in the gas. And
\(v_{boom}=3.4354*\cfrac{density}{m*(particle\,count\,per\,type)*(particle\,count\,per\,type)}\) --- (6)
for collisions between molecule clusters and singular molecule in a gas
And things get complicated, with many shadows.
The Problem With M
The expected \(m\) in,
\(P(energy\,state\,m)=e^{-\cfrac{E_a}{k.T_{boom}}}.\cfrac{\cfrac{1}{n^m}}{m!}\)
is,
\(E[m]=\sum^\infty_1{me^{-\cfrac{E_a}{k.T_{boom}}}.\cfrac{\cfrac{1}{n^m}}{m!}}\)
\(E[m]=e^{-\cfrac{E_a}{k.T_{boom}}}\sum^\infty_1{\cfrac{m\cfrac{1}{n^m}}{m!}}\)
From,
\(\sum^\infty_0 {k\cfrac{z^k}{k!}}=ze^z=\sum^\infty_1 {k\cfrac{z^k}{k!}}\)
because the term when \(k=0\) is zero.
\(E[m]=e^{-\cfrac{E_a}{k.T_{boom}}}\sum^\infty_1{\cfrac{m\cfrac{1}{n^m}}{m!}}=e^{-\cfrac{E_a}{k.T_{boom}}}.\cfrac{1}{n}e^{\cfrac{1}{n}}\)
But,
\(\cfrac{E_a}{kT_{boom}}=\cfrac{1}{n}\)
\(E[m]=\cfrac{1}{n}\)
What happened? \(P(energy\,state\,m)\) should have been \(P(energy\,state\,m,\,\cfrac{1}{m})\), but is the result still valid.
\(P(energy\,state\,m)\) is the probability of a particle being in the \(m\) energy state, that is, with thermal energy \(m\) times its kinetic energy.
\({kT_{boom}}={m}.{E_a}\)
In this result, \(E_a\) is not the energy state of the particle. But, the sum of thermal and kinetic energy, \(E\) is,
\(E=thermal\,energy+kinetic\,energy={kT_{boom}}+E_a\)
\(E=(m+1)E_a\)
Compared to Boltzmann Distribution,
\(F({\rm {state}})\propto e^{-{\frac {E}{kT}}}\)
\(P(energy\,state\,m)\) has an explicit discrete random variable \(m\), but is to be interpreted as the reciprocal of a energy multiple and its total energy is \(m+1\) multiple of its kinetic energy at a given temperature \(T_{boom}\).
In this dream world, all matter with temperature is nuclear, to a greater or less extent, depending on the fraction of particles with the most probable speed \(v_p=v_{boom}\) given \(T_{boom}\). All matter with temperature is radiating.
Temperature particles, \(T^{+}\) and \(T^{-}\) and charged particles, \(p^{+}\) and \(e^{-}\) are likely candidates in solids, in water and other polar liquid. Gravity particles, \(g^{+}\) and \(g^{-}\) in the case of crystalline solids.
\(P(energy\,state\,m)=e^{-\cfrac{E_a}{k.T_{boom}}}.\cfrac{\cfrac{1}{n^m}}{m!}\)
is,
\(E[m]=\sum^\infty_1{me^{-\cfrac{E_a}{k.T_{boom}}}.\cfrac{\cfrac{1}{n^m}}{m!}}\)
\(E[m]=e^{-\cfrac{E_a}{k.T_{boom}}}\sum^\infty_1{\cfrac{m\cfrac{1}{n^m}}{m!}}\)
From,
\(\sum^\infty_0 {k\cfrac{z^k}{k!}}=ze^z=\sum^\infty_1 {k\cfrac{z^k}{k!}}\)
because the term when \(k=0\) is zero.
\(E[m]=e^{-\cfrac{E_a}{k.T_{boom}}}\sum^\infty_1{\cfrac{m\cfrac{1}{n^m}}{m!}}=e^{-\cfrac{E_a}{k.T_{boom}}}.\cfrac{1}{n}e^{\cfrac{1}{n}}\)
But,
\(\cfrac{E_a}{kT_{boom}}=\cfrac{1}{n}\)
\(E[m]=\cfrac{1}{n}\)
What happened? \(P(energy\,state\,m)\) should have been \(P(energy\,state\,m,\,\cfrac{1}{m})\), but is the result still valid.
\(P(energy\,state\,m)\) is the probability of a particle being in the \(m\) energy state, that is, with thermal energy \(m\) times its kinetic energy.
\({kT_{boom}}={m}.{E_a}\)
In this result, \(E_a\) is not the energy state of the particle. But, the sum of thermal and kinetic energy, \(E\) is,
\(E=thermal\,energy+kinetic\,energy={kT_{boom}}+E_a\)
\(E=(m+1)E_a\)
Compared to Boltzmann Distribution,
\(F({\rm {state}})\propto e^{-{\frac {E}{kT}}}\)
\(P(energy\,state\,m)\) has an explicit discrete random variable \(m\), but is to be interpreted as the reciprocal of a energy multiple and its total energy is \(m+1\) multiple of its kinetic energy at a given temperature \(T_{boom}\).
In this dream world, all matter with temperature is nuclear, to a greater or less extent, depending on the fraction of particles with the most probable speed \(v_p=v_{boom}\) given \(T_{boom}\). All matter with temperature is radiating.
Temperature particles, \(T^{+}\) and \(T^{-}\) and charged particles, \(p^{+}\) and \(e^{-}\) are likely candidates in solids, in water and other polar liquid. Gravity particles, \(g^{+}\) and \(g^{-}\) in the case of crystalline solids.
Friday, November 17, 2017
An Old Friend For New Reasons
When \( v_{p}\) replaces \(v_{rms}\),
\(v_{p}=\sqrt{\cfrac{2RT_{boom}}{M_m}}\)
\(v^2_{boom}=v^2_{p}\) and
\(M_m\rightarrow nM_m\)
\(v^2_{boom}=\cfrac{2RT}{nM_m}\)
where \(n\) is due to clustering, when \(n\) particles coalesce and move as one,
\(n.\cfrac{1}{2}{M_m}v^2_{boom}={\cfrac{1}{2}*2R.T_{boom}}=R.T_{boom}\)
\(\cfrac{\cfrac{1}{2}{M_m}v^2_{boom}}{R.T_{boom}}=\cfrac{1}{n}\)
Let \(M_m=N.m_a\), \(N\)is the number in one mole and \(m_a\) is particle mass,
\(\cfrac{\cfrac{1}{2}{N.m_a}v^2_{boom}}{R.T_{boom}}=\cfrac{\cfrac{1}{2}{m_a}v^2_{boom}}{\cfrac{R}{N}T_{boom}}=\cfrac{1}{n}\)
Let \(E_a=\cfrac{1}{2}{m_a}v^2_{boom}\)
\(\cfrac{E_a}{kT_{boom}}=\cfrac{1}{n}\)
and we are back to Maxwell-Boltzmann, but as in the post "\(T_{boom}\) To The Power Of \(T_{boom}\)" dated 09 Nov 2017,
\(P(energy\,state\,m)=e^{-\cfrac{E_a}{k.T_{boom}}}.\cfrac{\cfrac{1}{n^m}}{m!}\)
Was Maxwell-Boltzmann measuring the most probable, and thus the maximum nuclear output due to \(T_{boom}\) in the first place?
If so, \(T_{boom}\) is \(T\) in Maxwell-Boltzmann distribution. We have been measuring \(T_{boom}\) as temperature already, all the time.
But \(T_{boom}\) is nuclear. It is not just an increase in temperature.
\(v_{p}=\sqrt{\cfrac{2RT_{boom}}{M_m}}\)
\(v^2_{boom}=v^2_{p}\) and
\(M_m\rightarrow nM_m\)
\(v^2_{boom}=\cfrac{2RT}{nM_m}\)
where \(n\) is due to clustering, when \(n\) particles coalesce and move as one,
\(n.\cfrac{1}{2}{M_m}v^2_{boom}={\cfrac{1}{2}*2R.T_{boom}}=R.T_{boom}\)
\(\cfrac{\cfrac{1}{2}{M_m}v^2_{boom}}{R.T_{boom}}=\cfrac{1}{n}\)
Let \(M_m=N.m_a\), \(N\)is the number in one mole and \(m_a\) is particle mass,
\(\cfrac{\cfrac{1}{2}{N.m_a}v^2_{boom}}{R.T_{boom}}=\cfrac{\cfrac{1}{2}{m_a}v^2_{boom}}{\cfrac{R}{N}T_{boom}}=\cfrac{1}{n}\)
Let \(E_a=\cfrac{1}{2}{m_a}v^2_{boom}\)
\(\cfrac{E_a}{kT_{boom}}=\cfrac{1}{n}\)
and we are back to Maxwell-Boltzmann, but as in the post "\(T_{boom}\) To The Power Of \(T_{boom}\)" dated 09 Nov 2017,
\(P(energy\,state\,m)=e^{-\cfrac{E_a}{k.T_{boom}}}.\cfrac{\cfrac{1}{n^m}}{m!}\)
Was Maxwell-Boltzmann measuring the most probable, and thus the maximum nuclear output due to \(T_{boom}\) in the first place?
If so, \(T_{boom}\) is \(T\) in Maxwell-Boltzmann distribution. We have been measuring \(T_{boom}\) as temperature already, all the time.
But \(T_{boom}\) is nuclear. It is not just an increase in temperature.
Wednesday, November 15, 2017
Who Decides Temp
This is \(ln(n)\) vs \(T_{boom}\) for Methane,
The negative gradient suggest \(n=Be^{-AT_{boom}}\) where \(A\) is the gradient of the line above and \(B=ln(y-intercept)\) a constant.
Then,
\(Temp=nT_{boom}=n.\cfrac{ln(\cfrac{B}{n})}{A}\) or \(Temp=-\cfrac{1}{A}n.ln(\cfrac{n}{B})\)
This is the way to relate \(n\) to Temp. But the density of the matter under study cannot be zero. For \(n\) to be valid \(T_{boom}\ne0\). The graph does not fit.
\(n\propto \cfrac{1}{T_{boom}}\)...
Given an average \(n\), \(Temp\propto T_{boom}\), that is why the previous posts on Methane suggests a series of \(ln(ln(ln(...))\).
\(n\) is the independent variable that determines \(Temp\) given \(T_{boom}\), something else set \(n\) and it is not \(Temp\). \(Temp\) is the result of \(n\) given \(T_{boom}\).
At the particle level, temperature jump at discrete steps as,
\(Temp=nT_{boom}\) or
\(\cfrac{E_a}{\cfrac{3}{2}kT_{boom}}=\cfrac{1}{n}\)
and \(n\) is an integer. But \(Temp\) given a volume of particles is a statistical average over all particles.
An we can all shower at the most comfortable temperature. Goodnight.
The negative gradient suggest \(n=Be^{-AT_{boom}}\) where \(A\) is the gradient of the line above and \(B=ln(y-intercept)\) a constant.
Then,
\(Temp=nT_{boom}=n.\cfrac{ln(\cfrac{B}{n})}{A}\) or \(Temp=-\cfrac{1}{A}n.ln(\cfrac{n}{B})\)
This is the way to relate \(n\) to Temp. But the density of the matter under study cannot be zero. For \(n\) to be valid \(T_{boom}\ne0\). The graph does not fit.
\(n\propto \cfrac{1}{T_{boom}}\)...
Given an average \(n\), \(Temp\propto T_{boom}\), that is why the previous posts on Methane suggests a series of \(ln(ln(ln(...))\).
\(n\) is the independent variable that determines \(Temp\) given \(T_{boom}\), something else set \(n\) and it is not \(Temp\). \(Temp\) is the result of \(n\) given \(T_{boom}\).
At the particle level, temperature jump at discrete steps as,
\(Temp=nT_{boom}\) or
\(\cfrac{E_a}{\cfrac{3}{2}kT_{boom}}=\cfrac{1}{n}\)
and \(n\) is an integer. But \(Temp\) given a volume of particles is a statistical average over all particles.
An we can all shower at the most comfortable temperature. Goodnight.
How Cold Can Two Get?
More Methane \(CH_4\) data,

What's more exponential than \(e^{T}\)? \(e^{T^2}\), \(e^{T^{T}}\)?
Temperature squared, \(Temp^2\) is not enough.
Data for the following graph was not printable. \(T^T\) was too big. Although the graph was still presented by the spreadsheet program. The graph is just a series of data points from 1 to 15 on the x axis.
Temperature to the power of temperature. Which make \(0^0=1\) a testable reality. But
\(ln(n)=1\) makes \(n=e=2.718\)
Is this the minimum \(n\) for Bose-Einstein condensate? \(\lfloor n \rfloor=2\)?
For any other \(n\), \(Temp\ne0\); temperature simply cannot be zero. This suggests that Absolute Zero is attainable only with a pair of particles. We have not considered the gradient and y-intercept of the regression line.
If the gradient is \(A\) and the y-intercept is \(C\) then,
\(ln(n_{0})=A.0^0+C\), \(n_{0}=e^{A+C}\)
which could be any number. We are still in trouble if Absolute Zero is achievable only with a specific number of particles.
Goodnight.

What's more exponential than \(e^{T}\)? \(e^{T^2}\), \(e^{T^{T}}\)?
Temperature squared, \(Temp^2\) is not enough.
Data for the following graph was not printable. \(T^T\) was too big. Although the graph was still presented by the spreadsheet program. The graph is just a series of data points from 1 to 15 on the x axis.
Temperature to the power of temperature. Which make \(0^0=1\) a testable reality. But
\(ln(n)=1\) makes \(n=e=2.718\)
Is this the minimum \(n\) for Bose-Einstein condensate? \(\lfloor n \rfloor=2\)?
For any other \(n\), \(Temp\ne0\); temperature simply cannot be zero. This suggests that Absolute Zero is attainable only with a pair of particles. We have not considered the gradient and y-intercept of the regression line.
If the gradient is \(A\) and the y-intercept is \(C\) then,
\(ln(n_{0})=A.0^0+C\), \(n_{0}=e^{A+C}\)
which could be any number. We are still in trouble if Absolute Zero is achievable only with a specific number of particles.
Goodnight.
Tuesday, November 14, 2017
Methane For The Restless
More data on \(n\) for Methane \(CH_4\) (from http://www.ddbst.com/en/EED/PCP/DEN_C1051.php),
And the graph of "exponential" increase in \(n\) with temperature is,
We are not getting anywhere, restlessly so.
| Temp (K) | Density (kg/m3) | v boom (m/s) | T boom (K) | n |
| 383.15 | 425.0 | 146.00 | 39.372 | 9.73 |
| 384.81 | 404.0 | 138.79 | 35.577 | 10.82 |
| 398.15 | 402.3 | 138.21 | 35.278 | 11.29 |
| 428.15 | 347.8 | 119.48 | 26.367 | 16.24 |
| 452.50 | 280.1 | 96.23 | 17.101 | 26.46 |
| 453.15 | 276.4 | 94.95 | 16.653 | 27.21 |
| 455.86 | 265.0 | 91.04 | 15.307 | 29.78 |
| 457.88 | 254.1 | 87.29 | 14.074 | 32.53 |
| 461.52 | 226.8 | 77.91 | 11.212 | 41.16 |
| 462.65 | 212.2 | 72.90 | 9.815 | 47.14 |
| 463.59 | 190.0 | 65.27 | 7.869 | 58.91 |
| 463.77 | 177.1 | 60.84 | 6.837 | 67.84 |
| 463.79 | 172.6 | 59.30 | 6.494 | 71.42 |
| 463.81 | 164.2 | 56.41 | 5.877 | 78.92 |
And the graph of "exponential" increase in \(n\) with temperature is,
We are not getting anywhere, restlessly so.
Monday, November 13, 2017
\(n\) Is Small
To put things into perspective, since particles are in the nano-meter range one million, \(n=10^{6}\) of them lined up end to end is about one millimeter.
If the matter has a solid or liquid state, \(n\gt 1\) is inevitable.
If the matter has a solid or liquid state, \(n\gt 1\) is inevitable.
Drunk Already, Enthanol
A even wider range of temp vs density values for ethanol is given below,
A graph of \(n\) vs Temp (K) is given below,
This set of data from https://www.thermalfluidscentral.org/encyclopedia/index.php/Thermophysical_Properties:_Ethanol shows the value of \(n\) decreases with high temperature. But the data does not agree with those in the previous posts "More Ethanol" dated 13 Nov 2017 and "Ethanol Boom Kills \(T_{boom}\) dated 10 Nov 2017 for lower values of temperature.
\(n\) drops throughout the temperature range presented.
| Temp (K) 513.15 | V boom (m/s) 0.415 | T boom (K) 54.83 | n 5.55 |
| 493.15 | 0.510 | 67.39 | 8.39 |
| 473.15 | 0.564 | 74.52 | 10.26 |
| 453.15 | 0.610 | 80.60 | 12.00 |
| 433.15 | 0.650 | 85.89 | 13.62 |
| 413.15 | 0.680 | 89.85 | 14.91 |
| 393.15 | 0.710 | 93.81 | 16.25 |
| 373.15 | 0.730 | 96.46 | 17.18 |
| 353.15 | 0.757 | 100.02 | 18.48 |
| 333.15 | 0.770 | 101.74 | 19.12 |
| 313.15 | 0.789 | 104.25 | 20.07 |
| 293.15 | 0.800 | 105.70 | 20.64 |
| 273.15 | 0.901 | 119.05 | 26.18 |
This set of data from https://www.thermalfluidscentral.org/encyclopedia/index.php/Thermophysical_Properties:_Ethanol shows the value of \(n\) decreases with high temperature. But the data does not agree with those in the previous posts "More Ethanol" dated 13 Nov 2017 and "Ethanol Boom Kills \(T_{boom}\) dated 10 Nov 2017 for lower values of temperature.
\(n\) drops throughout the temperature range presented.
More Ethanol
More extensive data for ethanol \(CH_3CH_2OH\) is presented below,
\(n\) increases as temperature increases throughout the range of temperature presented, and beyond the boiling point at \(351.39\,K\).
\(n\) increasing with temperature is consistent with increasing thermal energy \(\cfrac{3}{2}kT\) with temperature, but clustered particles seem intuitively less likely to increase in size with temperature. Increase in collisions is likely to break clustered particles apart. BUT density is decreasing, that means there is more space between particles as temperature increases. Maybe collisions decreases with lowered density and clustering increases with temperature as density drops, with more space between clustered particles.
Taken to higher temperature, before disintegration, clustering could result in large macro-molecules in high velocity. Is that possible? The least value of \(n\) is one, \(n\ge1\)
What is the nature of such clustering? Temperature particles acting like waves and coalesce? Is clustering electrostatic as the particles break from the lattice are positively charged.
Is \(n\) even valid?
| Temp (K) | Densityx10^3 (kg/m3) | v boom (m/s) | T boom (K) | n |
| 378.15 | 706 | 93.284 | 16.07 | 23.53 |
| 373.15 | 711 | 93.945 | 16.30 | 22.89 |
| 368.15 | 717 | 94.738 | 16.58 | 22.21 |
| 363.15 | 722 | 95.398 | 16.81 | 21.60 |
| 358.15 | 728 | 96.191 | 17.09 | 20.96 |
| 353.15 | 733 | 96.852 | 17.32 | 20.38 |
| 348.15 | 738 | 97.513 | 17.56 | 19.82 |
| 343.15 | 743 | 98.173 | 17.80 | 19.28 |
| 338.15 | 748 | 98.834 | 18.04 | 18.74 |
| 333.15 | 753 | 99.494 | 18.28 | 18.22 |
| 328.15 | 758 | 100.155 | 18.53 | 17.71 |
| 323.15 | 763 | 100.816 | 18.77 | 17.21 |
| 318.15 | 768 | 101.476 | 19.02 | 16.73 |
| 313.15 | 772 | 102.005 | 19.22 | 16.30 |
| 308.15 | 777 | 102.666 | 19.47 | 15.83 |
| 303.15 | 781 | 103.194 | 19.67 | 15.41 |
| 298.15 | 786 | 103.855 | 19.92 | 14.97 |
| 293.15 | 790 | 104.383 | 20.12 | 14.57 |
| 288.15 | 795 | 105.044 | 20.38 | 14.14 |
| 283.15 | 799 | 105.572 | 20.59 | 13.76 |
| 278.15 | 803 | 106.101 | 20.79 | 13.38 |
| 273.15 | 808 | 106.762 | 21.05 | 12.98 |
| 268.15 | 812 | 107.290 | 21.26 | 12.61 |
| 263.15 | 816 | 107.819 | 21.47 | 12.26 |
| 258.15 | 820 | 108.347 | 21.68 | 11.91 |
| 253.15 | 824 | 108.876 | 21.89 | 11.56 |
| 248.15 | 828 | 109.404 | 22.11 | 11.23 |
| 243.15 | 832 | 109.933 | 22.32 | 10.89 |
| 238.15 | 836 | 110.461 | 22.54 | 10.57 |
| 233.15 | 840 | 110.990 | 22.75 | 10.25 |
| 228.15 | 844 | 111.518 | 22.97 | 9.93 |
| 223.15 | 848 | 112.047 | 23.19 | 9.62 |
| 218.15 | 851 | 112.443 | 23.35 | 9.34 |
| 213.15 | 855 | 112.972 | 23.57 | 9.04 |
| 208.15 | 859 | 113.500 | 23.79 | 8.75 |
| 203.15 | 863 | 114.029 | 24.01 | 8.46 |
| 198.15 | 866 | 114.425 | 24.18 | 8.19 |
| 193.15 | 870 | 114.954 | 24.41 | 7.91 |
| 188.15 | 874 | 115.482 | 24.63 | 7.64 |
| 183.15 | 877 | 115.879 | 24.80 | 7.38 |
| 178.15 | 881 | 116.407 | 25.03 | 7.12 |
| 173.15 | 884 | 116.804 | 25.20 | 6.87 |
| 168.15 | 888 | 117.332 | 25.43 | 6.61 |
| 163.15 | 891 | 117.729 | 25.60 | 6.37 |
\(n\) increases as temperature increases throughout the range of temperature presented, and beyond the boiling point at \(351.39\,K\).
\(n\) increasing with temperature is consistent with increasing thermal energy \(\cfrac{3}{2}kT\) with temperature, but clustered particles seem intuitively less likely to increase in size with temperature. Increase in collisions is likely to break clustered particles apart. BUT density is decreasing, that means there is more space between particles as temperature increases. Maybe collisions decreases with lowered density and clustering increases with temperature as density drops, with more space between clustered particles.
Taken to higher temperature, before disintegration, clustering could result in large macro-molecules in high velocity. Is that possible? The least value of \(n\) is one, \(n\ge1\)
What is the nature of such clustering? Temperature particles acting like waves and coalesce? Is clustering electrostatic as the particles break from the lattice are positively charged.
Is \(n\) even valid?
Sunday, November 12, 2017
Freezing Is The Other Way
It seems paradoxical that \(n\) increases with temperature in all the material examined, water and ethanol. Although higher temperature is expected to be able to move larger cluster. The biggest cluster will be a completely aggregated solid. But freezing is in the other direction. This hypothetical aggregated solid at high temperature will have high velocity.
What else is there?
What else is there?
Look Sharp, A New Expression
From the updated post "\(T_{boom}\) To The Power Of \(T_{boom}\)" dated 09 Nov 2017, from which we have the notion that clustering elevate the thermal energy of a particle,
\(\cfrac{E_a}{\cfrac{3}{2}kT_{boom}}=\cfrac{1}{n}\)
at the same time the particle is actually an aggregate of \(n\) particles, at speed \(v_{boom}\).
This does not introduce new inventions into Kinetic Theory but is derived within Kinetic Theory with the application \(v_{boom}\). The mean state \(n\) is responsible for the existence and spread of discrete energy states, \(m\).
\(P(energy\,state\,m)=e^{-\cfrac{E_a}{k.\cfrac{3}{2}T_{boom}}}.\cfrac{\cfrac{1}{n^m}}{m!}\)
If a matter has a liquid state or a solid state, particles in it will bond to from aggregate and so the particles cluster. In the case of water, hydrogen bonds cluster the molecular particles.
This is not new, but the term \(\cfrac{1}{m!}\) does explain the deviation when \(m\) is high. In this expression the tail end of the graph is lowered by high values of \(m\). At the same time, \(T_{boom}\) axis is contracted by \(1.5\) (3D graph). These result in a much sharper graph.
Goodnight.
\(\cfrac{E_a}{\cfrac{3}{2}kT_{boom}}=\cfrac{1}{n}\)
at the same time the particle is actually an aggregate of \(n\) particles, at speed \(v_{boom}\).
This does not introduce new inventions into Kinetic Theory but is derived within Kinetic Theory with the application \(v_{boom}\). The mean state \(n\) is responsible for the existence and spread of discrete energy states, \(m\).
\(P(energy\,state\,m)=e^{-\cfrac{E_a}{k.\cfrac{3}{2}T_{boom}}}.\cfrac{\cfrac{1}{n^m}}{m!}\)
If a matter has a liquid state or a solid state, particles in it will bond to from aggregate and so the particles cluster. In the case of water, hydrogen bonds cluster the molecular particles.
This is not new, but the term \(\cfrac{1}{m!}\) does explain the deviation when \(m\) is high. In this expression the tail end of the graph is lowered by high values of \(m\). At the same time, \(T_{boom}\) axis is contracted by \(1.5\) (3D graph). These result in a much sharper graph.
Goodnight.
Iron Boiled At \(T_{boom\,p}\)
For Iron \(Fe\), \(Z=26\), molar mass of \(0.055845\,kgmol^{-1}\), density of \(7874\,kgm^{-3}\)
\(v_{boom}=3.4354*\cfrac{7874}{26}=1040.40\,ms^{-1}\)
\(T_{boom\,p}=\cfrac{1040.40^2*0.055845}{2*8.3144}=3635.16\,K\) or \(3362.01\,^oC\)
Iron has a melting point of \(1811\,K\) and a boiling point of \(3134 K\)
\(v_{boom}=3.4354*\cfrac{7874}{26}=1040.40\,ms^{-1}\)
\(T_{boom\,p}=\cfrac{1040.40^2*0.055845}{2*8.3144}=3635.16\,K\) or \(3362.01\,^oC\)
Iron has a melting point of \(1811\,K\) and a boiling point of \(3134 K\)
And the most nuclear \(T_{boom\,p}\) bring iron beyond its boiling point.
Friday, November 10, 2017
The Nuclear Cow is Driving...
\(T_{boom\,p}\) is when the matter is most nuclear, given density.
\(T_{boom\,p}=v^2_{boom}.\cfrac{M_m}{2R}\)
\(v_{boom}=3.4354*\cfrac{density}{Z}\)
Change in phase (melting and boiling) need not be at when the matter is most nuclear. But radiation from the matter is highest at this temperature, \(T_{boom\,p}\) when it is most nuclear. Such radiation is not derived from the heat source that warms the matter, but from \(v_{boom}\) within the matter. (post "A Small Boom" dated 16 Oct 2017)
And the nuclear cow drives the cart, looking for evidence..., the cart is still before the cow, nuclear or not.
\(T_{boom\,p}=v^2_{boom}.\cfrac{M_m}{2R}\)
\(v_{boom}=3.4354*\cfrac{density}{Z}\)
Change in phase (melting and boiling) need not be at when the matter is most nuclear. But radiation from the matter is highest at this temperature, \(T_{boom\,p}\) when it is most nuclear. Such radiation is not derived from the heat source that warms the matter, but from \(v_{boom}\) within the matter. (post "A Small Boom" dated 16 Oct 2017)
And the nuclear cow drives the cart, looking for evidence..., the cart is still before the cow, nuclear or not.
Coal Fire Again
The problem is Lignite (a form of coal) has a density of only \(801\,kgm^{-3}\) which would mean,
\(v_{boom\,lignite}=3.4354*\cfrac{801}{6}=458.63\,ms^{-1}\)
and
\(T_{p}=\cfrac{458.63^2*12.0107*10^{-3}}{2*8.3144}=151.93\,K\)
Lignite will spontaneously ignite at \(151.93-273.15=-121.22\,^oC\)! What happened? Apparently, lignite low density value is due to bulk (air space) and is not structural. The quoted density value is bulk density.
In the case of Anthracite, another form of coal, with a density value of \(1506\,kgm^{-3}\),
\(v_{boom\,anthracite}=3.4354*\cfrac{1506}{6}=862.29\,ms^{-1}\)
and
\(T_{862}=\cfrac{862.29^2*12.0107*10^{-3}}{2*8.3144}=537.04\,K\)
It will ignite at \(263.90\,^oC\)
And bituminous coal of a density \(1346\,kgm^{-3}\),
\(v_{\small{boom\,bituminous}}=3.4354*\cfrac{1346}{6}=770.67\,ms^{-1}\)
and
\(T_{770}=\cfrac{770.67^2*12.0107*10^{-3}}{2*8.3144}=428.98\,K\)
\(v_{boom\,lignite}=3.4354*\cfrac{801}{6}=458.63\,ms^{-1}\)
and
\(T_{p}=\cfrac{458.63^2*12.0107*10^{-3}}{2*8.3144}=151.93\,K\)
Lignite will spontaneously ignite at \(151.93-273.15=-121.22\,^oC\)! What happened? Apparently, lignite low density value is due to bulk (air space) and is not structural. The quoted density value is bulk density.
In the case of Anthracite, another form of coal, with a density value of \(1506\,kgm^{-3}\),
\(v_{boom\,anthracite}=3.4354*\cfrac{1506}{6}=862.29\,ms^{-1}\)
and
\(T_{862}=\cfrac{862.29^2*12.0107*10^{-3}}{2*8.3144}=537.04\,K\)
It will ignite at \(263.90\,^oC\)
And bituminous coal of a density \(1346\,kgm^{-3}\),
\(v_{\small{boom\,bituminous}}=3.4354*\cfrac{1346}{6}=770.67\,ms^{-1}\)
and
\(T_{770}=\cfrac{770.67^2*12.0107*10^{-3}}{2*8.3144}=428.98\,K\)
It will ignite at \(155.83\,^oC\).
And another quoted value of density for coal at \(1400\,kgm^{-3}\)
\(v_{\small{boom\,brown}}=3.4354*\cfrac{1400}{6}=801.59\,ms^{-1}\)
and
\(T_{770}=\cfrac{801.59^2*12.0107*10^{-3}}{2*8.3144}=464.10\,K\)
It ignites at \(190.95\,^oC\)
Crystalline (structural) density should be used and not bulk density in the calculations for \(v_{boom}\) and \(T_{v\,boom}\).
Do we need to differentiate \(v_{rms}\) and \(v_p\) and so, \(T_{v\,boom}\) and \(T_{boom\,p}\)?
Apparently you need to have most of the particles at \(v_{boom}\) (\(v_{p}=v_{boom}\)) to ignite the matter, and afterwards the matter settles to a temperature where the particles has a \(v_{rms}\) at \(v_{boom}\). ie. (\(v_{rms}=v_{boom}\)). In the former case, we are concerned with velocities at which most particles collide and in the latter, we are concerned with the mean of velocities squared of the particles as indicative of its energy content; the measured temperature according to Kinetic Theory for Ideal gases.
Speculative... still go put out the coal fire.
and
\(T_{770}=\cfrac{801.59^2*12.0107*10^{-3}}{2*8.3144}=464.10\,K\)
It ignites at \(190.95\,^oC\)
Crystalline (structural) density should be used and not bulk density in the calculations for \(v_{boom}\) and \(T_{v\,boom}\).
Do we need to differentiate \(v_{rms}\) and \(v_p\) and so, \(T_{v\,boom}\) and \(T_{boom\,p}\)?
Apparently you need to have most of the particles at \(v_{boom}\) (\(v_{p}=v_{boom}\)) to ignite the matter, and afterwards the matter settles to a temperature where the particles has a \(v_{rms}\) at \(v_{boom}\). ie. (\(v_{rms}=v_{boom}\)). In the former case, we are concerned with velocities at which most particles collide and in the latter, we are concerned with the mean of velocities squared of the particles as indicative of its energy content; the measured temperature according to Kinetic Theory for Ideal gases.
Speculative... still go put out the coal fire.
Hottest When Most Probable
\(T_{boom}\) being nuclear suggests that energy is generated in excess of energy input driving the matter to higher temperature. The velocities \(v\) of individual particles are, if we admit Kinetic Theory for ideal gas, distributed according to the Maxwell-Boltzmann distribution. The most probable velocity \(v_{p}\) is given by,
\(v_{p}=\sqrt{\cfrac{2RT}{M_m}}\) --- (*)
where \(T\), is the temperature when most particles attain \(v_{p}\)
If at \(v_{p}\), the particles are in resonance (post "A Small Boom" dated 16 Oct 2017) and is nuclear, then \(T_{boom\,p}\) is the temperature when the matter is most nuclear, probablistically.
\(v^2_{p}=\cfrac{2RT}{M_m}\)
but,
\(v^2_{rms}=\cfrac{3RT_{rms}}{M_m}=\cfrac{3}{2}v^2_{p}\)
If we set, \(v_{p}=v_{boom}\), then
\(v^2_{rms}=\cfrac{3}{2}v^2_{p}=\cfrac{3}{2}v^2_{boom}\)
and
\(T_{boom\,p}=T_{rms}=v^2_{rms}.\cfrac{M_m}{3R}=\cfrac{3}{2}v^2_{boom}.\cfrac{M_m}{3R}=\cfrac{3}{2}T_{boom}\)
Boiling or melting may not require the matter to be at its most nuclear. Sufficient energy to initiate a change in phase will do.
However, the rms value is likely the measured value of \(T\), as the average energy (root of the mean square value) content of the whole distribution profile. However, energy radiating from the matter will peak when \(v_{boom}\) is most probable, and so, when \(T=T_{boom\,p}\) the matter is most nuclear. Or simply from (*)
\(T_{boom\,p}=v^2_{boom}.\cfrac{M_m}{2R}\)
when \(v_{boom}=v_{p}\)
And we have to adjust all values of \(T_{boom}\) calculated previously.
Iron Melted At \(T_{boom}\)
Please be reminded of \(E=mc^2\). Small amount of mass is equivalent to huge amount of energy.
For Iron \(Fe\), \(Z=26\), molar mass of \(0.055845\,kgmol^{-1}\), density of \(7874\,kgm^{-3}\)
\(v_{rms}=3.4354*\cfrac{7874}{26}=1040.40\,ms^{-1}\)
\(T_{boom}=\cfrac{1040.40^2*0.055845}{3*8.3144}=2423.44\,K\) or \(2150.29\,^oC\)
Iron has a melting point of \(1811\,K\) and a boiling point of \(3134 K\)
What happens to iron at \(2423.44\,K\)? Red Hot? No, red hot in all shades are below the melting point.
The density of iron at \(2150.29\,^oC\) is expected to be different from \(7874\,kgm^{-3}\). So, what happens to iron around \(2150.29\,^oC\)? If at this temperature iron is completely sealed off from oxidizing does it remain at \(T_{boom}\)?
For Iron \(Fe\), \(Z=26\), molar mass of \(0.055845\,kgmol^{-1}\), density of \(7874\,kgm^{-3}\)
\(v_{rms}=3.4354*\cfrac{7874}{26}=1040.40\,ms^{-1}\)
\(T_{boom}=\cfrac{1040.40^2*0.055845}{3*8.3144}=2423.44\,K\) or \(2150.29\,^oC\)
Iron has a melting point of \(1811\,K\) and a boiling point of \(3134 K\)
What happens to iron at \(2423.44\,K\)? Red Hot? No, red hot in all shades are below the melting point.
The density of iron at \(2150.29\,^oC\) is expected to be different from \(7874\,kgm^{-3}\). So, what happens to iron around \(2150.29\,^oC\)? If at this temperature iron is completely sealed off from oxidizing does it remain at \(T_{boom}\)?
Cool Liquid Fuel Boom
\(T_{boom}\) for liquid fuel,
Kerosene \(C_{13.5}H_{29}\), molar mass of \(0.19136\,kgmol^{-1}\) and density \(795\,kgm^{-3}\)
\(v_{rms}=3.4354*795*\cfrac{1}{13.5*6+29*1}=24.83\,ms^{-1}\)
\(T_{boom}=\cfrac{24.83^2*0.19136}{3*8.3144}=4.729\,K\)
Base on another set of data Kerosene \(C_{12}H_{26}\), molar mass of \(0.17032\,kgmol^{-1}\) and density \(750\,kgm^{-3}\)
\(v_{rms}=3.4354*750*\cfrac{1}{12*6+26*1}=26.29\,ms^{-1}\)
\(T_{boom}=\cfrac{26.29^2*0.17032}{3*8.3144}=4.719\,K\)
Diesel \(C_{12}H_{24}\), molar mass of \(0.1683\,kgmol^{-1}\) and density \(840\,kgm^{-3}\)
\(v_{rms}=3.4354*840*\cfrac{1}{12*6+24*1}=30.05\,ms^{-1}\)
\(T_{boom}=\cfrac{24.83^2*0.1683}{3*8.3144}=6.225\,K\)
Kerosene \(C_{13.5}H_{29}\), molar mass of \(0.19136\,kgmol^{-1}\) and density \(795\,kgm^{-3}\)
\(v_{rms}=3.4354*795*\cfrac{1}{13.5*6+29*1}=24.83\,ms^{-1}\)
\(T_{boom}=\cfrac{24.83^2*0.19136}{3*8.3144}=4.729\,K\)
Base on another set of data Kerosene \(C_{12}H_{26}\), molar mass of \(0.17032\,kgmol^{-1}\) and density \(750\,kgm^{-3}\)
\(v_{rms}=3.4354*750*\cfrac{1}{12*6+26*1}=26.29\,ms^{-1}\)
\(T_{boom}=\cfrac{26.29^2*0.17032}{3*8.3144}=4.719\,K\)
Diesel \(C_{12}H_{24}\), molar mass of \(0.1683\,kgmol^{-1}\) and density \(840\,kgm^{-3}\)
\(v_{rms}=3.4354*840*\cfrac{1}{12*6+24*1}=30.05\,ms^{-1}\)
\(T_{boom}=\cfrac{24.83^2*0.1683}{3*8.3144}=6.225\,K\)
Gasoline \(C_{8}H_{18}\), molar mass of \(0.1142\,kgmol^{-1}\) and density \(719.7\,kgm^{-3}\)
\(v_{rms}=3.4354*719.7*\cfrac{1}{8*6+18*1}=37.46\,ms^{-1}\)
\(T_{boom}=\cfrac{37.46^2*0.1142}{3*8.3144}=6.560\,K\)
They are way cold. Very cold. By themselves, they are not indicative of any thing. Maybe they are resistance to further cooling.
\(v_{rms}=3.4354*719.7*\cfrac{1}{8*6+18*1}=37.46\,ms^{-1}\)
\(T_{boom}=\cfrac{37.46^2*0.1142}{3*8.3144}=6.560\,K\)
They are way cold. Very cold. By themselves, they are not indicative of any thing. Maybe they are resistance to further cooling.