野心燎世原
贪溺安份地
战掠非劳获
僚杀毁功德
自古恶受恶
刀客死刀下
《劝战》
正气绕心怀
单衣当护甲
意转日月轮
志焰焚侵兵
剑指化敌小
赤手摆乾坤!
《仙幻说》
Saturday, April 30, 2016
Killing Oscillations
It may be possible to kill oscillations quickly by applying a 180o phase wave form, or having removed the resonance driving force, applies a DC at the peak value of the oscillating sinusoidal.
It the case of a toaster, apply a DC voltage to the heating element with the oscillating voltage off. This DC voltage should be valued at the peak value of the oscillating voltage.
Anti-gravity too much!
It the case of a toaster, apply a DC voltage to the heating element with the oscillating voltage off. This DC voltage should be valued at the peak value of the oscillating voltage.
Anti-gravity too much!
The Rest Are In The Clouds
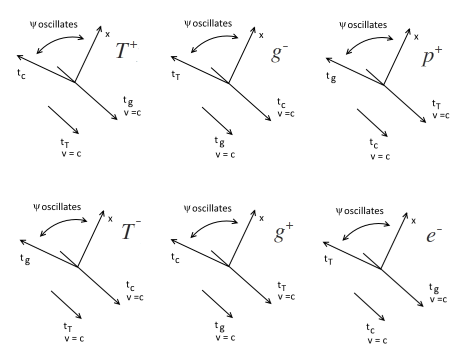
Under normal circumstances, only the outer protons held by the positive temperature particles' weak field acquire the opposite particles (electrons) in orbit. To balance the rest of the positive charge in the inner layers of the nucleus, a cloud of electrons orbit around nucleus just below the layer of positive temperature particles.
Both temperature and gravity particles also acquire opposite particles as a cloud of particles in orbit around the nucleus. The opposite particle cloud orbits just above the last respective positive particle layer. None of the orbiting cloud opposite particle is associated with a specific positive particle. This could account for the different statistics observed. Electrons associated with a specific orbiting proton displays Fermi–Dirac statistics and electrons in a cloud surrounding the nucleus at an inner layer just below the \(T^+\) particles displays Bose–Einstein statistics.
The rest are in the clouds. And so is retirement.
Both temperature and gravity particles also acquire opposite particles as a cloud of particles in orbit around the nucleus. The opposite particle cloud orbits just above the last respective positive particle layer. None of the orbiting cloud opposite particle is associated with a specific positive particle. This could account for the different statistics observed. Electrons associated with a specific orbiting proton displays Fermi–Dirac statistics and electrons in a cloud surrounding the nucleus at an inner layer just below the \(T^+\) particles displays Bose–Einstein statistics.
The rest are in the clouds. And so is retirement.
Particle Spectra Lines, Who's Flashing
From the post "Sizing Them Up" dated 3 Dec 2014,
One spectra line indicates the presence of two particles, one positive holding another negative particle in orbit. The spectra line is the result of a transition of the negative particle in the field of the corresponding type, from a higher to lower energy level.
The following diagram shows a driving force at a frequency \(f_d\), \(n\) integer times less than the system's natural frequency \(f_o\), being applied to the system.
The system is driven in phase repeatedly after every \(n\) cycle. It is still driven to resonance as long as \(n\) is an integer.
This means a force at frequency one million times less than 2466067.5 GHz, ie
\(f_d=\cfrac{f_o}{n}=2.46 GHz\)
\(n=10^6\)
will still drive the system into resonance and expel the orbiting negative particle. This is the microwave frequency used in an microwave oven. This suggests that the particle being driven off is a negative temperature particle. The remaining positive temperature particle at the nuclei is the reason that food heats up in a microwave oven. (A sponge cake can catch fire in an microwave oven suggests that something else other than agitated water is responsible for oven's heating effect. It is negative temperature particles being ejected from the material leaving behind positive temperature particles that causes temperature to rise.)
But there are four spectra lines and only three particles? The last two lines are from electron-proton pair in the outer most shell. At outermost shell the orbit pair can split into two unpaired orbit each at a higher energy level than when paired. The data set,
is due to an unpaired electron-proton orbit. The data set,
is due to a paired electron-proton orbit that requires more energy for energy level transition.
The existence of one other possible electron positions within the paired orbit configurations indicates the origin of double spectra lines and/or triple spectra lines.
The data set,
is then from a gravity particle pair. Driving off a negative gravity particle, results in an increase in gravitational potential.
It is not possible that an outer paired orbit unpairs without the lower shell also unpairing. If they do unpair correspondingly, then spectra lines due to the inner shell particles will also split into double lines or triple lines.
Have a nice day.
| \(a_{\psi}\) (nm) | f (GHz) | \(\lambda\) (nm) |
| 19.34 | 2466067.5 | 121.56701 |
| 16.32 | 2922728.6 | 102.5728 |
| 15.48 | 3082568.8 | 97.2541 |
| 14.77 | 3230699.3 | 92.79 |
One spectra line indicates the presence of two particles, one positive holding another negative particle in orbit. The spectra line is the result of a transition of the negative particle in the field of the corresponding type, from a higher to lower energy level.
The following diagram shows a driving force at a frequency \(f_d\), \(n\) integer times less than the system's natural frequency \(f_o\), being applied to the system.
The system is driven in phase repeatedly after every \(n\) cycle. It is still driven to resonance as long as \(n\) is an integer.
This means a force at frequency one million times less than 2466067.5 GHz, ie
\(f_d=\cfrac{f_o}{n}=2.46 GHz\)
\(n=10^6\)
will still drive the system into resonance and expel the orbiting negative particle. This is the microwave frequency used in an microwave oven. This suggests that the particle being driven off is a negative temperature particle. The remaining positive temperature particle at the nuclei is the reason that food heats up in a microwave oven. (A sponge cake can catch fire in an microwave oven suggests that something else other than agitated water is responsible for oven's heating effect. It is negative temperature particles being ejected from the material leaving behind positive temperature particles that causes temperature to rise.)
But there are four spectra lines and only three particles? The last two lines are from electron-proton pair in the outer most shell. At outermost shell the orbit pair can split into two unpaired orbit each at a higher energy level than when paired. The data set,
| \(a_{\psi}\) (nm) | f (GHz) | \(\lambda\) (nm) |
| 15.48 | 3082568.8 | 97.2541 |
is due to an unpaired electron-proton orbit. The data set,
| \(a_{\psi}\) (nm) | f (GHz) | \(\lambda\) (nm) |
| 14.77 | 3230699.3 | 92.79 |
is due to a paired electron-proton orbit that requires more energy for energy level transition.
The existence of one other possible electron positions within the paired orbit configurations indicates the origin of double spectra lines and/or triple spectra lines.
The data set,
| \(a_{\psi}\) (nm) | f (GHz) | \(\lambda\) (nm) |
| 16.32 | 2922728.6 | 102.5728 |
is then from a gravity particle pair. Driving off a negative gravity particle, results in an increase in gravitational potential.
It is not possible that an outer paired orbit unpairs without the lower shell also unpairing. If they do unpair correspondingly, then spectra lines due to the inner shell particles will also split into double lines or triple lines.
Have a nice day.
Electron Pool Dive!
If the work function is always half the bond energy, then
when an unpaired orbit acquires a fill electron, it is the proton that attracts the negative particle. Although it is just as probable that the positive side of the weak field acquires the negative particle.
The likelihood of each scenario depends on which configuration has lower energy. So, it is possible that,
when the orbit is unpaired, the negative particle jumps from orbit around the proton into the weak field with an release of energy, and vice versa.
When the work function is not half the bond energy, the negative particle is first acquired by the weak field. When a passing photon unpairs the orbits temporarily, it is possible that the electron jumps into weak field with an release of energy before the orbits pair up again with another release of energy.
And that's how the metal gets heated up.
Note: Within the metal, may or may not be covalent bond as we know it.
when an unpaired orbit acquires a fill electron, it is the proton that attracts the negative particle. Although it is just as probable that the positive side of the weak field acquires the negative particle.
The likelihood of each scenario depends on which configuration has lower energy. So, it is possible that,
when the orbit is unpaired, the negative particle jumps from orbit around the proton into the weak field with an release of energy, and vice versa.
When the work function is not half the bond energy, the negative particle is first acquired by the weak field. When a passing photon unpairs the orbits temporarily, it is possible that the electron jumps into weak field with an release of energy before the orbits pair up again with another release of energy.
And that's how the metal gets heated up.
Note: Within the metal, may or may not be covalent bond as we know it.
Thursday, April 14, 2016
Particle Creation And Destruction
How are particles destroyed? There has to be a destructive process to counter balance the creative process, so that there is a matter to energy transition and, energy to matter and matter to energy transitions are in equilibrium. As at now there is an over abundance of matter.
Wednesday, April 13, 2016
Whole Particles Creation And Quantum Splits
From the post "Missed Something..." dated 12 Apr 2016, electrons are created. As an electron in higher energy orbit is relaxed, it transit to a lower energy orbit and emits a packet of energy that is the difference in energy between the higher and lower orbits.
The requirement for integer number of wavelengths in stable valid orbits guarantees that this packet of energy emitted, forms into whole particles, because,
\(n\lambda=2\pi a_{\psi}\)
\(h=mc.n\lambda\)
Please refer to the post "\(\psi\) All Over The Place" dated 14 Jul 2015 and post "de Broglie Per Person" dated 20 Dec 2014,
\(E=hf=mc^2.n\) with \(c=f\lambda\) where \(n\) is an integer,
Energy difference from a higher orbit, \(m\) to a lower orbit, \(n\) where \(m\gt n\) ,
\(\Delta E=mc^2(m-n)\)
This is an integer multiple of \(mc^2\), thus in general, when the photon slows down in the respective field (\(E\) field for \(P_{e^{-}}\) photon), integer multiple of the particles are created.
Do the particles exist as an coalesce, one big particle of multiple magnitude or do the particles split into individuals immediately?
The particle is one with multiple magnitude. This answers the question posted on "Heavy Electrons" dated 17 Jul 2015, how do we make heavy electron?
The big particle can split via Quantum tunneling from the post "Two Quantum Wells, Quantum Tunneling, \(v_{min}\)" dated 19 Jul 2015, where from the beginning it is about a particle orbiting in the \(\psi\) of another particle of the same type, transiting to a higher orbit by itself. At the higher orbit the particles are further apart and thus one big particle splits.
The requirement for integer number of wavelengths in stable valid orbits guarantees that this packet of energy emitted, forms into whole particles, because,
\(n\lambda=2\pi a_{\psi}\)
\(h=mc.n\lambda\)
Please refer to the post "\(\psi\) All Over The Place" dated 14 Jul 2015 and post "de Broglie Per Person" dated 20 Dec 2014,
\(E=hf=mc^2.n\) with \(c=f\lambda\) where \(n\) is an integer,
Energy difference from a higher orbit, \(m\) to a lower orbit, \(n\) where \(m\gt n\) ,
\(\Delta E=mc^2(m-n)\)
This is an integer multiple of \(mc^2\), thus in general, when the photon slows down in the respective field (\(E\) field for \(P_{e^{-}}\) photon), integer multiple of the particles are created.
Do the particles exist as an coalesce, one big particle of multiple magnitude or do the particles split into individuals immediately?
The particle is one with multiple magnitude. This answers the question posted on "Heavy Electrons" dated 17 Jul 2015, how do we make heavy electron?
The big particle can split via Quantum tunneling from the post "Two Quantum Wells, Quantum Tunneling, \(v_{min}\)" dated 19 Jul 2015, where from the beginning it is about a particle orbiting in the \(\psi\) of another particle of the same type, transiting to a higher orbit by itself. At the higher orbit the particles are further apart and thus one big particle splits.
Daisy In A Daisy Field
In a similar way,
\(F_T=m_Ta\)
with
\(F_T=\cfrac{T_1T_2}{4\pi\tau_o r^2}\)
which is derived from the Gaussian flux concept (Gauss's Law) with \(\tau_o\) being analogous to \(\varepsilon_o\) and \(T_n\) the magnitude of the \(n\)th temperature particle analogous to charge. \(m_T\) is the mass of a temperature particle, its inertia in a \(T\) field. We might differentiate,
\(m_{T^{+}}\)
mass for a positive temperature particle and,
\(m_{T^{-}}\)
mass for a negative temperature particle.
Nice!
\(F_T=m_Ta\)
with
\(F_T=\cfrac{T_1T_2}{4\pi\tau_o r^2}\)
which is derived from the Gaussian flux concept (Gauss's Law) with \(\tau_o\) being analogous to \(\varepsilon_o\) and \(T_n\) the magnitude of the \(n\)th temperature particle analogous to charge. \(m_T\) is the mass of a temperature particle, its inertia in a \(T\) field. We might differentiate,
\(m_{T^{+}}\)
mass for a positive temperature particle and,
\(m_{T^{-}}\)
mass for a negative temperature particle.
Nice!
Tuesday, April 12, 2016
Mass Of Particle
Which get us to the difficult part, if ONLY \(g\) particles interacts with the gravitational field, what is \(m_e\) associated with a \(e^{-}\) particle? A
(\(g^{+}\), \(T^{+}\), \(e^{-}\))
particle would be as heavy as a neutron! Strictly speaking, an electron can only be moved by an electric force in an electric field and not by any physical force,
\(F\ne m_ea\)
But consider,
\(F_E=\cfrac{q_1q_2}{4\pi \varepsilon_o r^2}\) and,
\(V_E=\cfrac{q_1q_2}{4\pi \varepsilon_o r}\)
\(\cfrac{d\,V_E}{dt}=\cfrac{q_1q_2}{4\pi \varepsilon_o r^2}.-1.\cfrac{d\,r}{dt}=F_E.-1.\cfrac{d\,r}{dt}\)
The minus sign indicates that potential energy decreases in the direction of increasing \(r\). But the Newtonian force and the associated power is,
\(P=F.v=ma.v\) we have also assume that mass is time invariant here
So,
\(ma.v=F_E.\cfrac{d\,r}{dt}\)
where along a field line, \(v=\cfrac{d\,r}{dt}\), it is then possible that,
\(F_E=ma\) --- (*)
that is to say, in an electric field, it is possible to associate the product of a mass and an acceleration with the electric force, if we let \(v=\cfrac{d\,r}{dt}\) to be along a field line. This however is valid only in an electric field, where \(r\) is valid and we are moving along \(r\) a electric field line. Devoid of an electric field expression (*) is not valid.
Consider now,
\(\cfrac{d\,F_E}{dt}=\cfrac{q_1q_2}{4\pi \varepsilon_o r^3}.-2.\cfrac{d\,r}{dt}=F_E.-2.\cfrac{1}{r}\cfrac{d\,r}{dt}=F_E.-2.\cfrac{d\,ln(r)}{d\,t}\)
\(\cfrac{d\,F}{dt}=m\cfrac{d\,a}{dt}+a\cfrac{d\,m}{dt}\)
If we asume that \(\cfrac{d\,m}{dt}=0\), then,
\(m\cfrac{d\,a}{dt}=-2F_E\cfrac{d\,ln(r)}{d\,t}=ma\cfrac{d\{-2ln(r)\}}{d\,t}\)
\(\cfrac{d\,ln(a)}{dt}=\cfrac{d\,ln(r^{-2})}{d\,t}\)
\(ln(a)=ln(r^{-2})+lnA\) where \(ln(A)\) is constant of integration,
\(a=A.\cfrac{1}{r^2}\)
If \(A=\cfrac{1}{m}\cfrac{q_1q_2}{4\pi\varepsilon_o}\)
we once again obtain a consistent expression for \(F_E\) and so \(V_E\). In arriving at this expression, we have assumed,
\(\cfrac{d\,m}{dt}=0\)
that this, the associated mass \(m\), is time invariant. So, calculations for \(r\) along a field line using,
\(F_E=ma\)
\(m\) being a constant will give us the consistent answers for \(r\) and \(V_E\), given \(F_E\).
As such, it is possible to associate masses, \(m_e\) and \(m_p\) with the particles \(e^{-}\) and \(p^{+}\) respectively, but only in an electric field and all motions are restricted to be along the field lines.
\(wt=m_e.g\)
the weight of an electron, is strictly absurd.
(\(g^{+}\), \(T^{+}\), \(e^{-}\))
particle would be as heavy as a neutron! Strictly speaking, an electron can only be moved by an electric force in an electric field and not by any physical force,
\(F\ne m_ea\)
But consider,
\(F_E=\cfrac{q_1q_2}{4\pi \varepsilon_o r^2}\) and,
\(V_E=\cfrac{q_1q_2}{4\pi \varepsilon_o r}\)
\(\cfrac{d\,V_E}{dt}=\cfrac{q_1q_2}{4\pi \varepsilon_o r^2}.-1.\cfrac{d\,r}{dt}=F_E.-1.\cfrac{d\,r}{dt}\)
The minus sign indicates that potential energy decreases in the direction of increasing \(r\). But the Newtonian force and the associated power is,
\(P=F.v=ma.v\) we have also assume that mass is time invariant here
So,
\(ma.v=F_E.\cfrac{d\,r}{dt}\)
where along a field line, \(v=\cfrac{d\,r}{dt}\), it is then possible that,
\(F_E=ma\) --- (*)
that is to say, in an electric field, it is possible to associate the product of a mass and an acceleration with the electric force, if we let \(v=\cfrac{d\,r}{dt}\) to be along a field line. This however is valid only in an electric field, where \(r\) is valid and we are moving along \(r\) a electric field line. Devoid of an electric field expression (*) is not valid.
Consider now,
\(\cfrac{d\,F_E}{dt}=\cfrac{q_1q_2}{4\pi \varepsilon_o r^3}.-2.\cfrac{d\,r}{dt}=F_E.-2.\cfrac{1}{r}\cfrac{d\,r}{dt}=F_E.-2.\cfrac{d\,ln(r)}{d\,t}\)
\(\cfrac{d\,F}{dt}=m\cfrac{d\,a}{dt}+a\cfrac{d\,m}{dt}\)
If we asume that \(\cfrac{d\,m}{dt}=0\), then,
\(m\cfrac{d\,a}{dt}=-2F_E\cfrac{d\,ln(r)}{d\,t}=ma\cfrac{d\{-2ln(r)\}}{d\,t}\)
\(\cfrac{d\,ln(a)}{dt}=\cfrac{d\,ln(r^{-2})}{d\,t}\)
\(ln(a)=ln(r^{-2})+lnA\) where \(ln(A)\) is constant of integration,
\(a=A.\cfrac{1}{r^2}\)
If \(A=\cfrac{1}{m}\cfrac{q_1q_2}{4\pi\varepsilon_o}\)
we once again obtain a consistent expression for \(F_E\) and so \(V_E\). In arriving at this expression, we have assumed,
\(\cfrac{d\,m}{dt}=0\)
that this, the associated mass \(m\), is time invariant. So, calculations for \(r\) along a field line using,
\(F_E=ma\)
\(m\) being a constant will give us the consistent answers for \(r\) and \(V_E\), given \(F_E\).
As such, it is possible to associate masses, \(m_e\) and \(m_p\) with the particles \(e^{-}\) and \(p^{+}\) respectively, but only in an electric field and all motions are restricted to be along the field lines.
\(wt=m_e.g\)
the weight of an electron, is strictly absurd.
Missed Something...
\(E_P=P_{e^{-}}+KE\)
\(P_{e^{-}}\rightarrow e^{-}\), when the photon slows down in space in a electric field, energy is conserved, light speed in space convert to light speed in \(t_c\) without loss. The particle with light speed along \(t_c\) is an electron, \(e^{-}\). Energy to matter conversion,
\(E=mc^2\)
as part of photoelectric effect when the photon slows in the opposing electric field. If the stopping field is reversed no current is detected because no energy to matter conversion occurs.
\(E_P=m_ec^2+KE\)
the electron is detected as a current and a stopping voltage quantify its kinetic energy \(KE\).
Which answers the question, where did the ejected electron come from? The electron was created as energy, a photon, and as the photon slows in the opposing electric field, it is converted to matter, an electron. Furthermore,
\(P_{e^{-}}=m_ec^2=h.f\)
where \(h\) is Planck's constant.
\(m_e=\cfrac{h}{\lambda c}\)
\(m_e=\cfrac{\hbar}{a_{\psi} c}\) --- (*)
where \(\lambda=2\pi a_\psi\) from the post "\(\psi\) All Over The Place" dated 14 Jul 2015. \(a_\psi\) is the radius of a sphere containing \(\psi\) of the electron.
Note: In (*), \(m_e\) is mass density instead of mass. \(\frac{\hbar}{ c}\) can be interpreted as the total mass density of the particle to be spread along a radius \(a_{\psi}\). Mass density arises because we considered point particles of no dimension. Point particles have one dimension in time, they either exist or don't. However, as a point in space, point particle has mass density.
\(P_{e^{-}}\rightarrow e^{-}\), when the photon slows down in space in a electric field, energy is conserved, light speed in space convert to light speed in \(t_c\) without loss. The particle with light speed along \(t_c\) is an electron, \(e^{-}\). Energy to matter conversion,
\(E=mc^2\)
as part of photoelectric effect when the photon slows in the opposing electric field. If the stopping field is reversed no current is detected because no energy to matter conversion occurs.
\(E_P=m_ec^2+KE\)
the electron is detected as a current and a stopping voltage quantify its kinetic energy \(KE\).
Which answers the question, where did the ejected electron come from? The electron was created as energy, a photon, and as the photon slows in the opposing electric field, it is converted to matter, an electron. Furthermore,
\(P_{e^{-}}=m_ec^2=h.f\)
where \(h\) is Planck's constant.
\(m_e=\cfrac{h}{\lambda c}\)
\(m_e=\cfrac{\hbar}{a_{\psi} c}\) --- (*)
where \(\lambda=2\pi a_\psi\) from the post "\(\psi\) All Over The Place" dated 14 Jul 2015. \(a_\psi\) is the radius of a sphere containing \(\psi\) of the electron.
Note: In (*), \(m_e\) is mass density instead of mass. \(\frac{\hbar}{ c}\) can be interpreted as the total mass density of the particle to be spread along a radius \(a_{\psi}\). Mass density arises because we considered point particles of no dimension. Point particles have one dimension in time, they either exist or don't. However, as a point in space, point particle has mass density.
What We Have Always Suspected...Fodo
From the previous post "Energy Shadow Of A Dipole" dated 12 Apr 2016,
\(E_s ={ m }_{ e }c^{ 2 } \{C_o-f({ r}_{ ph })\}\)
where, \(f(r)=ln(r)-C.r\) and
\(C_o=f(r_s)\).
\(r_s\) is the normal radius of the electron around the proton that the electron return to after the passing of an incident photon; \(r_{ph}\) is the minimum radius of the orbit as the electron is pushed towards the proton when an incident photon passes through.
\(E_s ={ m }_{ e }c^{ 2 } \{C_o-f({ r}_{ ph })\}\)
where, \(f(r)=ln(r)-C.r\) and
\(C_o=f(r_s)\).
\(r_s\) is the normal radius of the electron around the proton that the electron return to after the passing of an incident photon; \(r_{ph}\) is the minimum radius of the orbit as the electron is pushed towards the proton when an incident photon passes through.
When \(r_s=r_{ph}\), ie that the electron is not pushed further towards the proton.
\(E_s =0\)
\(E_P=\cfrac{1}{2}E_b\) which is a constant.
We move \(r_{ph}\) towards \(r_s\) by decreasing the incident photon frequency.
\(E_P=constant\)
suggests that there is a minimum frequency of the incident photon that must provide for \(E_P=\frac{1}{2}E_b\), below which there is no emitted photon. \(E_P\) does not decrease continuously to zero with decreasing incident photon frequency.
\(E_P=\cfrac{1}{2}E_b=\Phi_w\)
From this we deduce that the work function, \(\Phi_w\) is half the bond energy.
Energy Shadow Of A Dipole
The difference in energy between two orbital state is emitted as a photon, \(P_{e^{-}}\)
along the line joining the spin orbit center and the positive particle center. The photon is being modeled as a dipole with a negative spinning end. The emitted photon need not pass through the proton, as the proton is in orbit and has moved. As both particles are relaxed after the photoelectric photon has passed, both return to their initial states, leave behind an energy shadow of a dipole with spinning negative field at one end and a positive field at the other. This energy shadow of a dipole is self propelled. It moves in direction of the positive end, perpendicular to the plane of the negative particle spin.
\(P_{e^{-}}\) is static calculation. We consider the situation to be the superposition of two parts, an electron orbiting around a proton at light speed, and a displacement of the center of this orbit along a line joining the proton and the center of the other orbit of the orbit pair. As the photoelectric photon passes the electron (orbiting at constant, light speed) is pushed towards the proton. From the post "Like Wave, Like Particle, Not Attracted to Electrons" dated 08 Jun 2014, the energy stored is,
\(E_s ={ m }_{ e }c^{ 2 } \{ln{( \cfrac{r_s}{{r }_{ ph}})}+C({ r}_{ ph }-{ r_s })\}\) --- (*)
The energy stored due to the displacement of the electron orbit center from the proton center is much more difficult because of the second weak field that holds the proton in place. Both weak fields are orientated to cancel each other. The resultant weak field is difficult to quantify.
If we consider the effect of the passing photon is to shield the electron completely from the distance weak field, then the negative particle returned to its original position around the proton, ie zero displacement, \(\small{d_{ph}=0}\). Then the energy stored due to displacement, \(E_d\) is the energy required to move the electron orbit to its normal position when the orbital separation is \(d\).
This should be half the bond formation energy as we are dealing with only one of the two pairs of particles involved. Where bond formation is assumed to be simply, two unpaired orbits moving into parallel position of separation \(d\).
\(E_d=\cfrac{1}{2}E_b\)
where \(E_b\) is the bond formation energy. So,
\(E_P=E_s+\cfrac{1}{2}E_b\)
where \(E_s\) is given by (*).
The resultant weak field has first to be quantified for an algebraic expression for \(E_d\). This is an simplification, because \(r_s\) would have changed as the particle is pushed towards the proton along the line joining the center of the other orbit and the proton. But this discrepancies is captured by \(E_b\), assuming that the electron is returned to its initial position as before the orbits are paired. The effect of the passing photoelectric photon is to unpair the paired orbits locally. In general, to include situation where such unpairing does not happen completely,
\(E_P\le E_s+\cfrac{1}{2}E_b\)
Have a nice day.
Note:
\(E_s ={ m }_{ e }c^{ 2 } \{ln{( \cfrac{r_s}{{r }_{ ph}})}+C({ r}_{ ph }-{ r_s })\}\\={ m }_{ e }c^{ 2 } \{f(r_s)-f({ r}_{ ph })\}\\={ m }_{ e }c^{ 2 } \{C_o-f({ r}_{ ph })\}\)
where, \(f(r)=ln(r)-C.r\) and \(C_o\) a constant for a given \(r_s\).
Illustrative plot of \(f(r)=ln(r)-C.r\) where \(C\lt0\).
along the line joining the spin orbit center and the positive particle center. The photon is being modeled as a dipole with a negative spinning end. The emitted photon need not pass through the proton, as the proton is in orbit and has moved. As both particles are relaxed after the photoelectric photon has passed, both return to their initial states, leave behind an energy shadow of a dipole with spinning negative field at one end and a positive field at the other. This energy shadow of a dipole is self propelled. It moves in direction of the positive end, perpendicular to the plane of the negative particle spin.
\(P_{e^{-}}\) is static calculation. We consider the situation to be the superposition of two parts, an electron orbiting around a proton at light speed, and a displacement of the center of this orbit along a line joining the proton and the center of the other orbit of the orbit pair. As the photoelectric photon passes the electron (orbiting at constant, light speed) is pushed towards the proton. From the post "Like Wave, Like Particle, Not Attracted to Electrons" dated 08 Jun 2014, the energy stored is,
\(E_s ={ m }_{ e }c^{ 2 } \{ln{( \cfrac{r_s}{{r }_{ ph}})}+C({ r}_{ ph }-{ r_s })\}\) --- (*)
The energy stored due to the displacement of the electron orbit center from the proton center is much more difficult because of the second weak field that holds the proton in place. Both weak fields are orientated to cancel each other. The resultant weak field is difficult to quantify.
If we consider the effect of the passing photon is to shield the electron completely from the distance weak field, then the negative particle returned to its original position around the proton, ie zero displacement, \(\small{d_{ph}=0}\). Then the energy stored due to displacement, \(E_d\) is the energy required to move the electron orbit to its normal position when the orbital separation is \(d\).
This should be half the bond formation energy as we are dealing with only one of the two pairs of particles involved. Where bond formation is assumed to be simply, two unpaired orbits moving into parallel position of separation \(d\).
\(E_d=\cfrac{1}{2}E_b\)
where \(E_b\) is the bond formation energy. So,
\(E_P=E_s+\cfrac{1}{2}E_b\)
where \(E_s\) is given by (*).
The resultant weak field has first to be quantified for an algebraic expression for \(E_d\). This is an simplification, because \(r_s\) would have changed as the particle is pushed towards the proton along the line joining the center of the other orbit and the proton. But this discrepancies is captured by \(E_b\), assuming that the electron is returned to its initial position as before the orbits are paired. The effect of the passing photoelectric photon is to unpair the paired orbits locally. In general, to include situation where such unpairing does not happen completely,
\(E_P\le E_s+\cfrac{1}{2}E_b\)
Have a nice day.
Note:
\(E_s ={ m }_{ e }c^{ 2 } \{ln{( \cfrac{r_s}{{r }_{ ph}})}+C({ r}_{ ph }-{ r_s })\}\\={ m }_{ e }c^{ 2 } \{f(r_s)-f({ r}_{ ph })\}\\={ m }_{ e }c^{ 2 } \{C_o-f({ r}_{ ph })\}\)
where, \(f(r)=ln(r)-C.r\) and \(C_o\) a constant for a given \(r_s\).
Illustrative plot of \(f(r)=ln(r)-C.r\) where \(C\lt0\).
Monday, April 11, 2016
Fluorescence Again? Photoelectric Pretending
This could be the path of the fill electron in one of the paired orbit,
but this would ignore the presence of the positive end of the weak field produce by a \(T^{+}\) particle on a layer just below. (This is likely the path of an electron in an unpaired orbit.) This weak field associated with the other orbit of the pair, together with the proton captured by the weak field of the current orbit, share the electron. If we superimpose the attraction from the proton and the weak field,
The electron spin around the proton is displaced towards the center of the other orbit in the pair.
The resultant spin of the negative particle generates a \(T\) / \(B\) field that is the oscillatory component of the photon emitted. The photon is thus emitted perpendicular to the plane of the electron spin.(???) This plane is perpendicular to the line joining the proton and the center of the other orbit of the pair. The center of the spin is along this line too. And,
\(tan(\theta)=\cfrac{d}{r}\)
where \(d\) is the orbital separation between the paired orbits and \(r\), the orbital radius.
We have encountered this before, in that case, two similar particles behaving like waves are attracted to each other, in the post "It's All Fluorescence Outside, Inside" dated 29 Jul 2015 and post "High Frequency EMW From Laser" dated 31 Jul 2015, etc
Note: Previously we have also taken the direction normal to the plane of spin as the direction of radiation. A loop of wire sends off EMW in the plane of its loop. It is the same for photons? How do a dipole leave energy behind and send off such energy? In both cases, whether photons are emitted parallel or perpendicular to the plane of the spin, the photons emitted still form a cone with apex angle \(2\theta\), given a particular viewing direction.
but this would ignore the presence of the positive end of the weak field produce by a \(T^{+}\) particle on a layer just below. (This is likely the path of an electron in an unpaired orbit.) This weak field associated with the other orbit of the pair, together with the proton captured by the weak field of the current orbit, share the electron. If we superimpose the attraction from the proton and the weak field,
The electron spin around the proton is displaced towards the center of the other orbit in the pair.
The resultant spin of the negative particle generates a \(T\) / \(B\) field that is the oscillatory component of the photon emitted. The photon is thus emitted perpendicular to the plane of the electron spin.(???) This plane is perpendicular to the line joining the proton and the center of the other orbit of the pair. The center of the spin is along this line too. And,
\(tan(\theta)=\cfrac{d}{r}\)
where \(d\) is the orbital separation between the paired orbits and \(r\), the orbital radius.
We have encountered this before, in that case, two similar particles behaving like waves are attracted to each other, in the post "It's All Fluorescence Outside, Inside" dated 29 Jul 2015 and post "High Frequency EMW From Laser" dated 31 Jul 2015, etc
Note: Previously we have also taken the direction normal to the plane of spin as the direction of radiation. A loop of wire sends off EMW in the plane of its loop. It is the same for photons? How do a dipole leave energy behind and send off such energy? In both cases, whether photons are emitted parallel or perpendicular to the plane of the spin, the photons emitted still form a cone with apex angle \(2\theta\), given a particular viewing direction.
Self-Balancing Furuma
This based on a Furuma (浮车),
where the fluid embedded with protons provides a self-balancing mechanism. A tilt on any side creates an accumulation of fluid and an excess of protons in motion, on that side.
The lifting force due to the particles increases and the craft recovers from the tilt.
Have a nice ride.
where the fluid embedded with protons provides a self-balancing mechanism. A tilt on any side creates an accumulation of fluid and an excess of protons in motion, on that side.
The lifting force due to the particles increases and the craft recovers from the tilt.
Have a nice ride.
Take Two On \(g_B\) And The Robinsons
Remember \(g_B\) from the post "Coriolis Force And My Left Foot" date 16 Nov 2014? This gravitation field could be the resultant weak field generated by the outer shell protons when the body is in circular motion. \(F_{gB}\) is the resultant Lorentz's force produced as the protons interact with \(g_B\) again.
Both the field \(g_B\), and the force \(F_{gB}\), are due to the macroscopic/aggregated motion of the protons in the body not mass per se.
We may deduce that a spinning disc produces a weak \(E_T\) field because of its \(T^{+}\) particles. This field interacts with the \(T^{+}\) particles again to produce a force \(F_{E_T}\). This is especially so when the outer \(T^{-}\) clouds are removed under high heat.
Similarly, a spinning disc produces a weak \(B_g\) field due to \(g^{+}\) particles and subsequently produces a force \(F_{B_g}\) when the \(g^{-}\) cloud are removed or reduced.
That aside, we have
the Robinsons. Positive charges on the hull of the flying saucer spin anti-clockwise to generate a \(g\) field upwards, as the whole saucer is spinning.
Fly!
Both the field \(g_B\), and the force \(F_{gB}\), are due to the macroscopic/aggregated motion of the protons in the body not mass per se.
We may deduce that a spinning disc produces a weak \(E_T\) field because of its \(T^{+}\) particles. This field interacts with the \(T^{+}\) particles again to produce a force \(F_{E_T}\). This is especially so when the outer \(T^{-}\) clouds are removed under high heat.
Similarly, a spinning disc produces a weak \(B_g\) field due to \(g^{+}\) particles and subsequently produces a force \(F_{B_g}\) when the \(g^{-}\) cloud are removed or reduced.
That aside, we have
the Robinsons. Positive charges on the hull of the flying saucer spin anti-clockwise to generate a \(g\) field upwards, as the whole saucer is spinning.
Fly!
Sunday, April 10, 2016
More Photons For More Fido Effects
An electron spinning at the end of a dipole being squeezed generates a \(T\) field.
This is the energy oscillating in the photon emitted by the dipole as the dipole is relaxed/released.
This is the energy oscillating in the photon emitted by the dipole as the dipole is relaxed/released.
In a similar way,
and
These are photons associated with each of the particle dipole. What happened to the complementary set of photons, where instead of the negative particles spinning, the positive particles are spinning?
Maybe in photoelectric effect (all dipole types) there is a small amount of energy (because of a low positive particle spin) being carried away by the corresponding complementary photon.
Saturday, April 9, 2016
Two New Worlds!
If our Sun, a fusion nuclear reactor full of \(p^{+}\), sends off \(p^{+}\) particles. Does a black hole full of \(g^{+}\) particles radiates \(g^{+}\) particles.
The question leading to this, was the nucleic set
(\(g^{+}\), \(T^{+}\), \(p^{+}\))
Why is \(p^{+}\) at the outer shell complemented by \(e^{-}\) particle? Equally probable is,
(\(p^{+}\), \(g^{+}\), \(T^{+}\))
where at the outer shell, \(T^{-}\) fills the orbit at the opposite end of the weak \(T\) field that holds the \(T^{+}\) particles. And the case in point,
(\(T^{+}\), \(p^{+}\), \(g^{+}\))
where at the outer shell, \(g^{-}\) fills the orbit at the opposite end of the weak \(g\) field that holds the \(g^{+}\) particles.
So we have a new kind of matter of a different type of nucleus, (\(T^{+}\), \(p^{+}\), \(g^{+}\)), whose chemical reactions center around the exchange and sharing of \(g^{-}\) particles. Planets of this new matter orbit around a black hole. And life forms of this new matter on such planets thinking about the possibility of total extinction.
Two new worlds!
What is a dense concentration of \(T^{+}\) particles. A White Dwarfs? A white dwarf nucleus; white dwarf matter; white dwarf planets; white dwarf alien life forms.
Note: Why is \(p^{+}\) at the outer shell complemented by \(e^{-}\) particle? Our Sun made us so.
The question leading to this, was the nucleic set
(\(g^{+}\), \(T^{+}\), \(p^{+}\))
Why is \(p^{+}\) at the outer shell complemented by \(e^{-}\) particle? Equally probable is,
(\(p^{+}\), \(g^{+}\), \(T^{+}\))
where at the outer shell, \(T^{-}\) fills the orbit at the opposite end of the weak \(T\) field that holds the \(T^{+}\) particles. And the case in point,
(\(T^{+}\), \(p^{+}\), \(g^{+}\))
where at the outer shell, \(g^{-}\) fills the orbit at the opposite end of the weak \(g\) field that holds the \(g^{+}\) particles.
So we have a new kind of matter of a different type of nucleus, (\(T^{+}\), \(p^{+}\), \(g^{+}\)), whose chemical reactions center around the exchange and sharing of \(g^{-}\) particles. Planets of this new matter orbit around a black hole. And life forms of this new matter on such planets thinking about the possibility of total extinction.
Two new worlds!
What is a dense concentration of \(T^{+}\) particles. A White Dwarfs? A white dwarf nucleus; white dwarf matter; white dwarf planets; white dwarf alien life forms.
Note: Why is \(p^{+}\) at the outer shell complemented by \(e^{-}\) particle? Our Sun made us so.
Looking For Ah Subb
Shouldn't Planet Nine be on the other side,
seems more consistent with the phrase "the other icy objects are being pulled to it ".
Anyone can play this game.
Note: Plato is still there!
seems more consistent with the phrase "the other icy objects are being pulled to it ".
Anyone can play this game.
Note: Plato is still there!
Only If You Have Been There
Sorry about the shakes, but I am close.
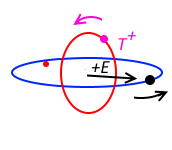
In a similar way to \(T^{-}\) particles subjected to heat, when \(g^{-}\)particles are subjected to high gravity, they are released from the \(g^{-}\) clouds around the nucleus. They pair up with free \(g^{+}\) particles,
and spins around the positive particle. They create a weak \(E\) field in the plane perpendicular to their spins. It is this \(E\) field that is responsible for the tingling sensations on the skin when you dropped from zero into high gravity.
Till the last singularity!
In a similar way to \(T^{-}\) particles subjected to heat, when \(g^{-}\)particles are subjected to high gravity, they are released from the \(g^{-}\) clouds around the nucleus. They pair up with free \(g^{+}\) particles,
and spins around the positive particle. They create a weak \(E\) field in the plane perpendicular to their spins. It is this \(E\) field that is responsible for the tingling sensations on the skin when you dropped from zero into high gravity.
Till the last singularity!
Good Bye Positive One
It could be that shielding under the outermost layer ejects the proton and the \(Cl\) nucleus retains a net negative charge,
and an anion is formed.
This will be the last post.
and an anion is formed.
This will be the last post.
\(T^{-}\) Source Cloud
The \(T^{-}\) clouds around the nucleus is the source of \(T^{-}\) particles when heat is apply. These particle are released from the nucleus at high temperature and is responsible for the boiling phenomenon, gas molecules' anti-gravity capability and the loss of magnetism with temperature. Please see posts "Wind, Eddies, Vortices And Turbulence" dated 16 Oct 2016 and "Magnetism And Temperature Particles" dated 11 Jul 2015.
Killing A Lot Of People At Once
The problem with Uranium is, it is not the best,
The proton shielding might attract an approaching electron, but the electron cloud below repels any negative charge. The other negative particle clouds \(g^{-}\) and \(T^{-}\) are above this electron cloud.
All negative particles can trigger a nucleic disintegration. The trick is to get as far into the nucleus as possible.
(\(T^{-}\), \(g^{-}\), \(e^{-}\))
This particle has an outer electron, holding it in orbit is a spinning \(g^{-}\) particle that generates a weak \(E\) field. A \(T^{-}\) particle spins in the core and holds the \(g^{-}\) particle with a weak \(g\) field. Such a particle will penetrate into Uranium, \(Ur\) as far as the electron cloud, unimpeded. The particle disintegrate and the other negative particles are freed within the nucleus.
This will probably just strip the outer layers of the atom. Further impacts might disintegrate the nucleus.
A chain reaction not!
The proton shielding might attract an approaching electron, but the electron cloud below repels any negative charge. The other negative particle clouds \(g^{-}\) and \(T^{-}\) are above this electron cloud.
All negative particles can trigger a nucleic disintegration. The trick is to get as far into the nucleus as possible.
(\(T^{-}\), \(g^{-}\), \(e^{-}\))
This particle has an outer electron, holding it in orbit is a spinning \(g^{-}\) particle that generates a weak \(E\) field. A \(T^{-}\) particle spins in the core and holds the \(g^{-}\) particle with a weak \(g\) field. Such a particle will penetrate into Uranium, \(Ur\) as far as the electron cloud, unimpeded. The particle disintegrate and the other negative particles are freed within the nucleus.
This will probably just strip the outer layers of the atom. Further impacts might disintegrate the nucleus.
A chain reaction not!
Friday, April 8, 2016
Where \(B\) Orbits Is
From Einstein's photoelectric effects, the post "Miss e- Miss e- Not" dated 04 Jun 2014,
we updated ourselves that a passing photon in a helical path squeeze an orbiting electron in a paired parallel orbit. The electron is brought close to the proton on the other orbit, \(d\) the distance between the orbits reduces. Previous calculations for atomic radius that was much smaller than measured atomic radius was actually for \(d\), the orbital separation.
Does the photoelectric effect apply to the electron cloud under the paired orbits? Yes, but at lower frequency, in the infra-red region.
Paired orbit is also the origin of \(B\) orbit that could explain away ultraviolet catastrophe. Unpaired orbit actually produces ultraviolet catastrophe, but few in numbers they leave a faint signature on most experimental data.
we updated ourselves that a passing photon in a helical path squeeze an orbiting electron in a paired parallel orbit. The electron is brought close to the proton on the other orbit, \(d\) the distance between the orbits reduces. Previous calculations for atomic radius that was much smaller than measured atomic radius was actually for \(d\), the orbital separation.
Does the photoelectric effect apply to the electron cloud under the paired orbits? Yes, but at lower frequency, in the infra-red region.
Paired orbit is also the origin of \(B\) orbit that could explain away ultraviolet catastrophe. Unpaired orbit actually produces ultraviolet catastrophe, but few in numbers they leave a faint signature on most experimental data.
Stolen Cracks!
we have instead a nucleus set as (\(g^{+}\), \(p^{+}\)), \(T^{+}\) particles are not bound to the nucleus. And the set (\(T^{+}\), \(p^{+}\), \(g^{+}\), \(p^{+}\)) is really interesting. This sign assignment does not generate a recurring set. But Earth as a \(g^{-}\) particle is most appealing given the direction of Earth's spin. It consistently generates a magnetic field where the field lines return to the North pole.
Dipoles Again!
None of the musings put forth here have been proven true.
There is a significance to the two opposing dipoles in orbit...
Remember posts "All Creatures Great and Small" and "Just Lots of Colors, Retro Disco" both dated 21 May 2014, where photons are modeled as dipoles and their resonance derived. The post "Background = Most Pervasive = Resonnace" dated 13 Apr 2014 where space was in resonance and was modeled like a spring; \(k_{space}\), the spring constant for space was derived (although it is equally possible that the peak in microwave radiation background is due to the source).
It could be that, this is the original dipole that case its shadow everywhere,
the dipole that resides in the orbit around the nucleus. This is the dipole that photons in photoelectric effects phenomenon interact with. This is the dipole that generates photons.
Photons are energy shadows from this dipole. This suggests, one of the ways to obtain energy from particles it to form a dipole of that type of particle and, squeeze and ease. In resonance the dipole will emit high energy photons.
What are the nature of photons from a (\(g^{-}\), \(g^{+}\)) dipole, (\(T^{-}\), \(T^{+}\)) dipole and, a ( \(e^{-}\), \(p^{+}\)) dipole that is consistent with the model of particles here?
There is a significance to the two opposing dipoles in orbit...
Remember posts "All Creatures Great and Small" and "Just Lots of Colors, Retro Disco" both dated 21 May 2014, where photons are modeled as dipoles and their resonance derived. The post "Background = Most Pervasive = Resonnace" dated 13 Apr 2014 where space was in resonance and was modeled like a spring; \(k_{space}\), the spring constant for space was derived (although it is equally possible that the peak in microwave radiation background is due to the source).
It could be that, this is the original dipole that case its shadow everywhere,
the dipole that resides in the orbit around the nucleus. This is the dipole that photons in photoelectric effects phenomenon interact with. This is the dipole that generates photons.
Photons are energy shadows from this dipole. This suggests, one of the ways to obtain energy from particles it to form a dipole of that type of particle and, squeeze and ease. In resonance the dipole will emit high energy photons.
What are the nature of photons from a (\(g^{-}\), \(g^{+}\)) dipole, (\(T^{-}\), \(T^{+}\)) dipole and, a ( \(e^{-}\), \(p^{+}\)) dipole that is consistent with the model of particles here?
Cloud Nine
Where is the electron cloud with respect to paired orbit shielding?
The paired orbits acquire their filled electron. The nucleus just below has a net negative particle imbalance. In order not to interfere with the weak fields holding protons at the outer layer, it is likely that the electron clouds be below the spinning \(T^{+}\) particles.
A filled paired orbit does not generate a weak field. A filled outer orbit shell ends the nucleus layers. Neither \(g^{-}\) and \(T^{-}\) particles fill their respective positive orbits. To balance the nucleus both type of negative particles exist as clouds around the nucleus. For the case of the nucleus set (\(g^{+}\),\(T^{+}\), \(p^{+}\)), \(T^{-}\) particle cloud exist just outside of the \(p^{+}\) orbital shell and \(g^{-}\) particle cloud is just outside of the \(T^{+}\) orbital shell. This is such that the negative particle clouds do not interfere with the weak fields that hold the next layer of the nucleus.
Cloud nine is mental. Good night.
Note: Can the electron cloud be beyond \(p^{+}\) shell? No, the cloud will then interfere with bond formations discussed thus far. Why is it possible that the electron cloud drop below the \(p^{+}\) shell? The \(p^{+}\) orbits in the outer shell can acquire their filled electron to balance the charge. They do not need to hold a next higher layer shell.
The paired orbits acquire their filled electron. The nucleus just below has a net negative particle imbalance. In order not to interfere with the weak fields holding protons at the outer layer, it is likely that the electron clouds be below the spinning \(T^{+}\) particles.
A filled paired orbit does not generate a weak field. A filled outer orbit shell ends the nucleus layers. Neither \(g^{-}\) and \(T^{-}\) particles fill their respective positive orbits. To balance the nucleus both type of negative particles exist as clouds around the nucleus. For the case of the nucleus set (\(g^{+}\),\(T^{+}\), \(p^{+}\)), \(T^{-}\) particle cloud exist just outside of the \(p^{+}\) orbital shell and \(g^{-}\) particle cloud is just outside of the \(T^{+}\) orbital shell. This is such that the negative particle clouds do not interfere with the weak fields that hold the next layer of the nucleus.
Cloud nine is mental. Good night.
Note: Can the electron cloud be beyond \(p^{+}\) shell? No, the cloud will then interfere with bond formations discussed thus far. Why is it possible that the electron cloud drop below the \(p^{+}\) shell? The \(p^{+}\) orbits in the outer shell can acquire their filled electron to balance the charge. They do not need to hold a next higher layer shell.
See You Not
It is likely that the unpaired orbit with an unbalanced weak field extend further than the other paired orbits. The filled paired orbits shield the lone proton from the electron at the positive end of the holding weak field.
The proton acquires another electron and \(Cl\) gains a negative charge to become \(Cl^{-}\).
Speculative as always...
In general, nucleus with many paired orbits can shield unpaired orbits from their filled electron and allow them to acquire another electron in their immediate vicinity. This results in an anion.
Note: The other case where the weak field holds two electrons is ruled out because of the strong repulsion between the electrons. In the above case, the extra electron is held by the proton and repulsed by the weak field. Shielding reduces the weak field further. It is likely that the lone electron held by the weak field, be within the shielding provided by the filled paired orbits.
The proton acquires another electron and \(Cl\) gains a negative charge to become \(Cl^{-}\).
Speculative as always...
In general, nucleus with many paired orbits can shield unpaired orbits from their filled electron and allow them to acquire another electron in their immediate vicinity. This results in an anion.
Note: The other case where the weak field holds two electrons is ruled out because of the strong repulsion between the electrons. In the above case, the extra electron is held by the proton and repulsed by the weak field. Shielding reduces the weak field further. It is likely that the lone electron held by the weak field, be within the shielding provided by the filled paired orbits.
And Chlorine Asks For More...
Notice the one but very glaring proton outside of \(Na\) nucleus! Are such protons responsible for the metallic sheen? Along this same line of madness, proton accelerates to photon.
But first,
How does \(Cl\) gain an electron to become \(Cl^{-}\)? Obviously,
But how? And more importantly why? And not so obviously,
Yes! It is making fun of you.
As stated before diffotoms, where the inner orbital structure of the element is different, are responsible for varied oxidation states.
In the case of \(ClO_{4}^{-}\) with \(Cl^{+7}\), the outer \(n=3\) swapped with inner \(n=4\), each of the four outer paired orbits bonds with a Oxygen leaving the unpaired orbit outside. This outer unpaired orbit gains an electron and the ions gains a negative charge.
In the case of \(Cl_2O_6\) with \(Cl^{+6}\), the unpaired orbits of two Chlorine pairs up and bond an Oxygen. Each of the three paired orbits of one of the Chlorine bonds an Oxygen. The other Chlorine bonds with two other Oxygen.
In the case of \(ClO^{-}_3\) with \(Cl^{+5}\), the outer \(n=3\) shell bonds with three Oxygen. The unpaired orbit gains an extra electron and the ion gains a negative charge.
In the case of \(ClO_2\) with \(Cl^{+4}\), the inner \(n=4\) shell moves to the outer layer and bonds with two Oxygen. The filled unpaired orbit rest in the lower layer.
In the case of \(ClO^{-}_{2}\) with \(Cl^{+3}\), the outer \(n=3\) shell bonds with two Oxygen. The unpaired orbit gains an extra electron and the ion gains a negative charge.
In the case of \(ClO^{-}\) with \(Cl^{+1}\), the outer \(n=3\) shell bonds with an Oxygen. The unpaired orbit gains an extra electron and the ion gains a negative charge.
Quantum number \(n=1,2,3,4..\) are all valid solutions. This means, around a nucleus there can be one, two, three, four...paired orbits. An unpaired orbit is also a solution, but has a single spin number.
Still, how does \(Cl\) gain an electron to become \(Cl^{-}\)?
But first,
How does \(Cl\) gain an electron to become \(Cl^{-}\)? Obviously,
But how? And more importantly why? And not so obviously,
Yes! It is making fun of you.
As stated before diffotoms, where the inner orbital structure of the element is different, are responsible for varied oxidation states.
In the case of \(ClO_{4}^{-}\) with \(Cl^{+7}\), the outer \(n=3\) swapped with inner \(n=4\), each of the four outer paired orbits bonds with a Oxygen leaving the unpaired orbit outside. This outer unpaired orbit gains an electron and the ions gains a negative charge.
In the case of \(Cl_2O_6\) with \(Cl^{+6}\), the unpaired orbits of two Chlorine pairs up and bond an Oxygen. Each of the three paired orbits of one of the Chlorine bonds an Oxygen. The other Chlorine bonds with two other Oxygen.
In the case of \(ClO^{-}_3\) with \(Cl^{+5}\), the outer \(n=3\) shell bonds with three Oxygen. The unpaired orbit gains an extra electron and the ion gains a negative charge.
In the case of \(ClO_2\) with \(Cl^{+4}\), the inner \(n=4\) shell moves to the outer layer and bonds with two Oxygen. The filled unpaired orbit rest in the lower layer.
In the case of \(ClO^{-}_{2}\) with \(Cl^{+3}\), the outer \(n=3\) shell bonds with two Oxygen. The unpaired orbit gains an extra electron and the ion gains a negative charge.
Quantum number \(n=1,2,3,4..\) are all valid solutions. This means, around a nucleus there can be one, two, three, four...paired orbits. An unpaired orbit is also a solution, but has a single spin number.
Still, how does \(Cl\) gain an electron to become \(Cl^{-}\)?
Charge Accounting, Free Orbits, Nuclei Shielding And Captions
A single positive and negative particle balanced (one of each, filled), unpaired orbit still has weak fields. These field holds the next layer of the nucleus together. A filled, paired orbit however, do not have weak fields. It can no longer hold the next particle for the nucleus. The interior of the nucleus therefore cannot hold negative particles, not for all paired orbits. There must be non zero resultant weak fields at the lower layer to hold particles on the next layer.
We are then left with a negative-positive particle imbalance. If we confine ourselves to electrons and protons, then the nucleus is positively charged. For a neutral atom, free negative charges orbit around the nucleus beyond the positive particle orbits.
Since within the nucleus there are positively filled paired orbits with weak fields that attract negative particles, it is possible such fields reach beyond the the outer layer and are responsible for the force holding the free negative particles in orbits. However,
Field lines will tend to terminate on the respective particles, a paired orbit with both negative and positive particles will shield any field lines from reaching beyond the paired orbit. This shielding confines radiated energy within the outer paired orbits and is responsible for preventing the inner orbits from collapsing.
In general, free negative particles orbits around the nucleus as expected.
How does then, Sodium, \(Na\) looses an electron and be \(Na^{+}\)?
Simple, but as always twisted. The single unpaired orbit of Sodium does not provide adequate shielding. The positive end of the weak fields from positively filled, paired orbits (the same fields that hold the positive particles in orbit, not the weak fields of the immediate orbiting positive particles) reaches outwards beyond the outer layer and attracts a corresponding negative particle. The negative particle orbits around the nucleus closer than the outer layer. This layer of negative particles lifts the potential of the single negative particle in the outer orbit and this particle leaves readily. When the negative particle is ejected, \(Na^{+}\) is formed.
Inadequate shielding of the \(Ne\) nucleus draws the ten free orbiting electrons closer and, shielding due to these ten electrons pushes the single outer shell electron further away.
Would the ten electrons be draw into the paired orbits? No, the directed weak field that holds the positive particle and draws the negative particle are from a inner layer. This field is weaken as the orbit pairs up. An unpaired orbit will attract a negative particle to its positive end more readily. The weak field generated by the immediate orbiting positive particle is an orthogonal field and do not interact with the negative particle. In the case of \(p^{+}\), the field generated is a \(g\) field and do attract an \(e^{-}\).
In general, all atoms with an inner electron cloud that pushes outer orbital electrons to higher potentials tend to ionize and be captions.
Next stop anions...Mind the gap!
Notes: filled orbit: both negative and positive particles in the orbit.
positively filled orbit: only positive particles in the orbit.
paired orbits: two orbits in parallel, very close, filled or positively filled.
unpaired orbits: one orbit, filled or positively filled.
We are then left with a negative-positive particle imbalance. If we confine ourselves to electrons and protons, then the nucleus is positively charged. For a neutral atom, free negative charges orbit around the nucleus beyond the positive particle orbits.
Since within the nucleus there are positively filled paired orbits with weak fields that attract negative particles, it is possible such fields reach beyond the the outer layer and are responsible for the force holding the free negative particles in orbits. However,
Field lines will tend to terminate on the respective particles, a paired orbit with both negative and positive particles will shield any field lines from reaching beyond the paired orbit. This shielding confines radiated energy within the outer paired orbits and is responsible for preventing the inner orbits from collapsing.
In general, free negative particles orbits around the nucleus as expected.
How does then, Sodium, \(Na\) looses an electron and be \(Na^{+}\)?
Simple, but as always twisted. The single unpaired orbit of Sodium does not provide adequate shielding. The positive end of the weak fields from positively filled, paired orbits (the same fields that hold the positive particles in orbit, not the weak fields of the immediate orbiting positive particles) reaches outwards beyond the outer layer and attracts a corresponding negative particle. The negative particle orbits around the nucleus closer than the outer layer. This layer of negative particles lifts the potential of the single negative particle in the outer orbit and this particle leaves readily. When the negative particle is ejected, \(Na^{+}\) is formed.
Inadequate shielding of the \(Ne\) nucleus draws the ten free orbiting electrons closer and, shielding due to these ten electrons pushes the single outer shell electron further away.
Would the ten electrons be draw into the paired orbits? No, the directed weak field that holds the positive particle and draws the negative particle are from a inner layer. This field is weaken as the orbit pairs up. An unpaired orbit will attract a negative particle to its positive end more readily. The weak field generated by the immediate orbiting positive particle is an orthogonal field and do not interact with the negative particle. In the case of \(p^{+}\), the field generated is a \(g\) field and do attract an \(e^{-}\).
In general, all atoms with an inner electron cloud that pushes outer orbital electrons to higher potentials tend to ionize and be captions.
Next stop anions...Mind the gap!
Notes: filled orbit: both negative and positive particles in the orbit.
positively filled orbit: only positive particles in the orbit.
paired orbits: two orbits in parallel, very close, filled or positively filled.
unpaired orbits: one orbit, filled or positively filled.
Killing Fields
When two unpaired orbits line up, the dipole switches direction from perpendicular to the axis of orbital rotation to parallel to the axis of orbital rotation,
this kills both weak fields along the axis of rotation.
Is there a radial field in the separation between the two orbits? Because the dipoles are opposing and spinning in the same sense, no. On average over a period of one revolution, there is no resultant radial field through the separation between the two orbits.
this kills both weak fields along the axis of rotation.
Is there a radial field in the separation between the two orbits? Because the dipoles are opposing and spinning in the same sense, no. On average over a period of one revolution, there is no resultant radial field through the separation between the two orbits.
Too Many, Some New...
The problem with such a nucleus construction scheme is that there are too many elements that proton or the opposite particle, electron, the configurations of which can account for.
Nor is the interaction between elements solely electron-proton. All other negative-positive particle pair can interact and present a new type of chemistry; gravity particle chemistry and temperature particle chemistry.
Luckily, just before you throw away your textbooks,
in this model opposite particles creates orthogonal fields, not opposite fields when they spin. When two opposite particles in parallel orbits are brought closer, they form a dipole. Their static fields reduce towards zero outside of the confine of the orbit, but they generate weak fields that do not cancels. If these particles are charges are they radiating EMW?
When the opposite particles forms a dipole and spins, their weak fields do not cancel. When another dipole is brought closer and place inverted to cancel with the first. The static field around the paired orbit is further reduced towards zero. No significant wave propagate through the static field. But do the weak fields doubles?
The key to this is the spinning \(E\) field across the dipole (in the case of electron and proton).
Nor is the interaction between elements solely electron-proton. All other negative-positive particle pair can interact and present a new type of chemistry; gravity particle chemistry and temperature particle chemistry.
Luckily, just before you throw away your textbooks,
in this model opposite particles creates orthogonal fields, not opposite fields when they spin. When two opposite particles in parallel orbits are brought closer, they form a dipole. Their static fields reduce towards zero outside of the confine of the orbit, but they generate weak fields that do not cancels. If these particles are charges are they radiating EMW?
When the opposite particles forms a dipole and spins, their weak fields do not cancel. When another dipole is brought closer and place inverted to cancel with the first. The static field around the paired orbit is further reduced towards zero. No significant wave propagate through the static field. But do the weak fields doubles?
The key to this is the spinning \(E\) field across the dipole (in the case of electron and proton).
Thursday, April 7, 2016
For One For All
Does a \(Ne\) nucleus exist? Yes, the paired orbits all without opposite particles, each generates a weak \(g\) field that sums to the resultant represented by the dotted arrow.
At the negative end of this weak field, a \(g^{+}\) particle spins as the nucleus spins. This is the start of the nucleus cyclic set (\(g^{+}\), \(T^{+}\), \(p^{+}\)), as the next layer to the nucleus.
All \(n\) solutions can have a resultant weak field extending beyond the nucleus.
At the negative end of this weak field, a \(g^{+}\) particle spins as the nucleus spins. This is the start of the nucleus cyclic set (\(g^{+}\), \(T^{+}\), \(p^{+}\)), as the next layer to the nucleus.
All \(n\) solutions can have a resultant weak field extending beyond the nucleus.
Free to Lift Reactor, Recycle
There is another solution to counter \(g^{+}\) particles, that is to let the reactor float and allow the particles to be conducted away at the top.
Without being attached at the bottom the reactor will not tear as it is lifted up.
Elements, boron has one pair orbit and one unpaired orbit, silver has one unpaired orbit, indium has one pair orbit and one unpaired orbit, and cadmium has one unpaired orbit. All these elements have a relatively uncrowded valence shell. The outer \(p^{+}\) particles in orbits generate a weak \(g\) field that will attract \(g^{+}\) particles. These \(g^{+}\) particles are neutralized by \(g^{-}\) particles. When \(g^{-}\) particles are in spin they generate weak \(E\) fields that are attracted to a higher absolute potential (since the weak fields are a directed fields and the particles are free to rotate, either positive or negative \(E\) field will attract them but it must be a stronger field). The elements are also conductive of electricity in order that a high potential be established for the flow of \(g^{-}\) particles into the reactor core to neutralize the \(g^{+}\) absorbed. This is to reduce swelling as the rods absorb \(g^{+}\) particles. Since only spinning \(g^{-}\) particles move towards a high potential,
the control rod should have a spin to induce similar motion on the passing particles.
\(g^{+}\) particles in spin generate a \(T\)/\(B\) field. A strong magnet will attract the particles and extract them from the control rods. Heat can first separate the two opposite particles and then the positive and negative gravity particles sent into spins by a spinning magnetic field, \(B\) and a spinning electric field, \(E\) respectively. The particles are attracted/separated by strong \(B\) and \(E\) fields, one at each end of the rod.
Both positive and negative \(g\) particles are removed from the rod.
Without being attached at the bottom the reactor will not tear as it is lifted up.
Elements, boron has one pair orbit and one unpaired orbit, silver has one unpaired orbit, indium has one pair orbit and one unpaired orbit, and cadmium has one unpaired orbit. All these elements have a relatively uncrowded valence shell. The outer \(p^{+}\) particles in orbits generate a weak \(g\) field that will attract \(g^{+}\) particles. These \(g^{+}\) particles are neutralized by \(g^{-}\) particles. When \(g^{-}\) particles are in spin they generate weak \(E\) fields that are attracted to a higher absolute potential (since the weak fields are a directed fields and the particles are free to rotate, either positive or negative \(E\) field will attract them but it must be a stronger field). The elements are also conductive of electricity in order that a high potential be established for the flow of \(g^{-}\) particles into the reactor core to neutralize the \(g^{+}\) absorbed. This is to reduce swelling as the rods absorb \(g^{+}\) particles. Since only spinning \(g^{-}\) particles move towards a high potential,
the control rod should have a spin to induce similar motion on the passing particles.
\(g^{+}\) particles in spin generate a \(T\)/\(B\) field. A strong magnet will attract the particles and extract them from the control rods. Heat can first separate the two opposite particles and then the positive and negative gravity particles sent into spins by a spinning magnetic field, \(B\) and a spinning electric field, \(E\) respectively. The particles are attracted/separated by strong \(B\) and \(E\) fields, one at each end of the rod.
Both positive and negative \(g\) particles are removed from the rod.
A \(g^{+}\) Detector
A simple weight sensor that detects a sudden decrease in weight,
when hit by \(g^{+}\) particles. The outer sensor surface should be dense to absorb incoming particles. An algorithm that process the data from the sensor can compensate for any swing in the device. The particles are likely to leave the device at a rate that hold the amount of particles within the surface constant, given the rate of impact of the particles. The amount of particles on hold in the device (on the sensor surface) is detected as a loss in weight and indicates the rate of impact of the \(g^{+}\) particles. It is expected that any thing with mass can conduct the \( g^{+}\) particles from the sensor surface and force a reset of the device.
Good night.
when hit by \(g^{+}\) particles. The outer sensor surface should be dense to absorb incoming particles. An algorithm that process the data from the sensor can compensate for any swing in the device. The particles are likely to leave the device at a rate that hold the amount of particles within the surface constant, given the rate of impact of the particles. The amount of particles on hold in the device (on the sensor surface) is detected as a loss in weight and indicates the rate of impact of the \(g^{+}\) particles. It is expected that any thing with mass can conduct the \( g^{+}\) particles from the sensor surface and force a reset of the device.
Good night.
Nuclear Chain Reaction
A nuclear chain reaction is when the collapse of the nucleus generates enough opposite/negative particles that lead to the further collapse of other nuclei. The nucleus itself has to have large numbers of weak field sites upon which the opposite/negative particles can trigger a collapse.
A sustained nuclear reaction is then one that generates enough opposite/negative particles for the reaction to proceed at a constant rate.
A controlled nuclear process is then one that is able to control (increase/decrease) the number of opposite/negative particles in the reaction.
Run away! I am nuclear.
What then are boron, silver, indium and cadmium as control rods and what are neutrons? If we are looking at heavy metal as nuclear fuel, then electrons are probably the negative particles of interest and protons, the generators of weak \(g\) fields sites at the nucleus; at least at the on start. Upon initiation, opposite/negative particles released from the nucleus trigger further nuclear disintegration. If neutrons are \(g^{+}\) particles then they have nothing to do with triggering this process of nuclear collapse described here.
A sustained nuclear reaction is then one that generates enough opposite/negative particles for the reaction to proceed at a constant rate.
A controlled nuclear process is then one that is able to control (increase/decrease) the number of opposite/negative particles in the reaction.
Run away! I am nuclear.
What then are boron, silver, indium and cadmium as control rods and what are neutrons? If we are looking at heavy metal as nuclear fuel, then electrons are probably the negative particles of interest and protons, the generators of weak \(g\) fields sites at the nucleus; at least at the on start. Upon initiation, opposite/negative particles released from the nucleus trigger further nuclear disintegration. If neutrons are \(g^{+}\) particles then they have nothing to do with triggering this process of nuclear collapse described here.
Come back! I am not nuclear just foolish.
Note: \(g^{+}\) particle increases gravitation potential locally. When interior parts of any structure are lifted up, horizontal cracks can appears. And that's how they crack up. \(g^{+}\) particles are regulated for this different reason. \(T^{+}\) is heat. A reactor do not crack because of a faulty temperature gauge. A \(g^{+}\) particle detector is needed. \(e^{-}\) is the key particle to control nuclear rate of reaction. \(p^{+}\) is probably the blue hue photons.
Nuclear Disintegration On Demand
When an orbit that acquires an opposite particle looses its weak field, it can no longer hold the upper layer particle. Within the nucleus, therefore, there cannot be any misplaced opposite/negative particles that negates the weak fields.
If we shoot opposite/negative particles into a nucleus, it is possible to destroy the weak fields and collapse the nucleus.
In the case of a positive particle nucleus, negative particles \(e^{-}\), \(g^{-}\) and \(T^{-}\) shot into the nucleus can kill the nucleus.
Kaboom!
If we shoot opposite/negative particles into a nucleus, it is possible to destroy the weak fields and collapse the nucleus.
In the case of a positive particle nucleus, negative particles \(e^{-}\), \(g^{-}\) and \(T^{-}\) shot into the nucleus can kill the nucleus.
Kaboom!
That's How We Double Up
In general for any type of particles \(c\), \(g\) and \(T\), the weak field moments generated by the revolving particles in a paired orbit cancel. For this reason, the bond is not radiating energy.
But, what if the orbit is unpaired? Weak field moment is not zero as the revolving opposite particles do not generate the same weak field but weak fields that are orthogonal.
What if the orbit does not have an opposite particle? Does radiating weak field wave kills off the spin? No, the weak field wave generated by the single particle in orbit slows down an passing opposite particle on its approach to the orbit. As shown in the diagram below, in the plane parallel to the orbit, the opposite particle is slowed by the weak field as the result of Lorentz Force, \(F\). \(F\) acts to slow the tangential velocity \(v\). The opposite particle will be given the same spin as the particle in orbit. This spinning opposite particle generates a weak field opposite to the particle in orbit and is slowed in the direction along the weak field on its approach to the orbit.
This is how the orbiting particle proactively attracts an opposite spinning particle. It slows the particle down. This opposite particle is captured by the opposite end of the weak field (generated by a \(T^{+}\) particle) holding the other particle on the orbit.
When both particles are in orbit, they spin as a dipole. Both generate a weak field that is orthogonal to each other, the weak fields do not cancel.
What motivate covalent bond formation then? When the opposite particle is removed (orbit ionized), instead of attracting an opposite particle, the weak field attracts the field weak of another orbit. As the weak fields merge both orbiting particles are spinning in the same sense and are repelled by each other to across the diameter of the orbit.
These paired orbits then attracts two opposite particles in the manner as described above.
We have a covalent bond, but still both unpaired orbits that form the bond must first be ionized (ie. opposite particle removed) before being paired. The opposite particles are attracted back to the orbits after the orbits paired up.
So, a covalent bond requires double the ionization energy of a unpaired orbit to initiate.
Good night.
But, what if the orbit is unpaired? Weak field moment is not zero as the revolving opposite particles do not generate the same weak field but weak fields that are orthogonal.
What if the orbit does not have an opposite particle? Does radiating weak field wave kills off the spin? No, the weak field wave generated by the single particle in orbit slows down an passing opposite particle on its approach to the orbit. As shown in the diagram below, in the plane parallel to the orbit, the opposite particle is slowed by the weak field as the result of Lorentz Force, \(F\). \(F\) acts to slow the tangential velocity \(v\). The opposite particle will be given the same spin as the particle in orbit. This spinning opposite particle generates a weak field opposite to the particle in orbit and is slowed in the direction along the weak field on its approach to the orbit.
This is how the orbiting particle proactively attracts an opposite spinning particle. It slows the particle down. This opposite particle is captured by the opposite end of the weak field (generated by a \(T^{+}\) particle) holding the other particle on the orbit.
When both particles are in orbit, they spin as a dipole. Both generate a weak field that is orthogonal to each other, the weak fields do not cancel.
What motivate covalent bond formation then? When the opposite particle is removed (orbit ionized), instead of attracting an opposite particle, the weak field attracts the field weak of another orbit. As the weak fields merge both orbiting particles are spinning in the same sense and are repelled by each other to across the diameter of the orbit.
These paired orbits then attracts two opposite particles in the manner as described above.
We have a covalent bond, but still both unpaired orbits that form the bond must first be ionized (ie. opposite particle removed) before being paired. The opposite particles are attracted back to the orbits after the orbits paired up.
So, a covalent bond requires double the ionization energy of a unpaired orbit to initiate.
Good night.
Bond Energy
So far, one chemical covalent bond involves four particles,
two proton orbits with two protons and two electrons attracted to each orbit by both the positive end of a weak \(E\) fields and the positive charge, proton, at the negative end of the weak \(E\) field. This weak field is produced by a spinning \(T^{+}\) particle.
And so, the bond energy of a single chemical covalent bond is...
\(U_{E}=-\cfrac{q}{4\pi\varepsilon_o}\left(\cfrac{1}{d}+\cfrac{1}{2r}-\cfrac{1}{\sqrt{d^2+4r^2}}\right)\)
where \(q=\left| e^{+} \right|=\left| p^{+} \right| \), that both particles have equal charge.
\(U_{wE}=-\cfrac{q_{T^{+}}}{4\pi\varepsilon_o}.\cfrac{1}{r}\)
where \(q_{T^{+}}\) is the equivalent charge that would establish the weak \(E\) field due to the spinning \(T^{+}\) particle on the next lower layer of the nucleus. It is expected that,
\(q_{T^{+}}\lt q^{+}\)
Although the particles are orbiting, they are static with respect to one another. The weak field holds the particles in place and the whole field rotates as the plane of the orbit of the \(T^{+}\) particle spins. In this case, bond energy is taken to be the energy required to remove of any one of the four particles.
\(U_{cov}=U_{E}+U_{wE}=-\cfrac{1}{4\pi\varepsilon_o}\left\{q\left(\cfrac{1}{d}+\cfrac{1}{2r}-\cfrac{1}{\sqrt{d^2+4r^2}}\right)-\cfrac{q_{T^{+}}}{r}\right\}\)
where \(U_{cov}\) is the covalent bond energy. Given that,
\(d\lt\lt r\)
\(U_{cov}\) is largely dependent on \(\frac{1}{d}\); that the separation \(d\) between the paired orbits determines bond energy and not the bond length taken as \(\small{2r}\).
The magnetic field generated by the revolving particles in the paired orbit cancel (post "Killing Fields""dated 8 Apr 2016),
\(U_{B}=0\)
For this reason, the bond is not radiating \(\small{EMW}\).
Given the positions of the negative charges, there might be measurable magnetic moment as the opposing fields do not cancel completely. In general, any forces changing the positions of the charge particles will result in a change in the magnetic moment of the bond.
Note: Chemical here implies electron and proton (the charge particles pair) interaction.
two proton orbits with two protons and two electrons attracted to each orbit by both the positive end of a weak \(E\) fields and the positive charge, proton, at the negative end of the weak \(E\) field. This weak field is produced by a spinning \(T^{+}\) particle.
And so, the bond energy of a single chemical covalent bond is...
\(U_{E}=-\cfrac{q}{4\pi\varepsilon_o}\left(\cfrac{1}{d}+\cfrac{1}{2r}-\cfrac{1}{\sqrt{d^2+4r^2}}\right)\)
where \(q=\left| e^{+} \right|=\left| p^{+} \right| \), that both particles have equal charge.
\(U_{wE}=-\cfrac{q_{T^{+}}}{4\pi\varepsilon_o}.\cfrac{1}{r}\)
where \(q_{T^{+}}\) is the equivalent charge that would establish the weak \(E\) field due to the spinning \(T^{+}\) particle on the next lower layer of the nucleus. It is expected that,
\(q_{T^{+}}\lt q^{+}\)
Although the particles are orbiting, they are static with respect to one another. The weak field holds the particles in place and the whole field rotates as the plane of the orbit of the \(T^{+}\) particle spins. In this case, bond energy is taken to be the energy required to remove of any one of the four particles.
\(U_{cov}=U_{E}+U_{wE}=-\cfrac{1}{4\pi\varepsilon_o}\left\{q\left(\cfrac{1}{d}+\cfrac{1}{2r}-\cfrac{1}{\sqrt{d^2+4r^2}}\right)-\cfrac{q_{T^{+}}}{r}\right\}\)
where \(U_{cov}\) is the covalent bond energy. Given that,
\(d\lt\lt r\)
\(U_{cov}\) is largely dependent on \(\frac{1}{d}\); that the separation \(d\) between the paired orbits determines bond energy and not the bond length taken as \(\small{2r}\).
\(U_{B}=0\)
For this reason, the bond is not radiating \(\small{EMW}\).
Given the positions of the negative charges, there might be measurable magnetic moment as the opposing fields do not cancel completely. In general, any forces changing the positions of the charge particles will result in a change in the magnetic moment of the bond.
Note: Chemical here implies electron and proton (the charge particles pair) interaction.
And She Does The Split!
More poison but where is triple bond?

Carbon monoxide, none of the five pairs of orbits \(n=5\), stands out to be counted as part of triple bond.
Unfortunately,
This is not valid for carbon dioxide, \(CO_2\). As the molecule is linear, but in that case, the center \(C\) does not have a valid Quantum Number. There is however another solution,
Carbon has an \(n=2\). Two Oxygen atoms are bonded to the Carbon orbits that are perpendicular to each other. But being free to rotate, one of the orbits rotates by \(90^o\), still rotating in a plane perpendicular to the other orbit pair and spreads the two oxygen atoms furthest apart. The molecule is then linear.
Hew!

Carbon monoxide, none of the five pairs of orbits \(n=5\), stands out to be counted as part of triple bond.
Unfortunately,
This is not valid for carbon dioxide, \(CO_2\). As the molecule is linear, but in that case, the center \(C\) does not have a valid Quantum Number. There is however another solution,
Carbon has an \(n=2\). Two Oxygen atoms are bonded to the Carbon orbits that are perpendicular to each other. But being free to rotate, one of the orbits rotates by \(90^o\), still rotating in a plane perpendicular to the other orbit pair and spreads the two oxygen atoms furthest apart. The molecule is then linear.
Hew!