If we now consider a space density profile around a planet,
\( { d }_{ s }(x)={ e }^{ -\cfrac { x }{ r } }({ d }_{ e }-{ d }_{ n })+{ d }_{ n }\)
where \(r\) is the radius of the planet, \({d}_{n}\) is a constant, the baseline space density of empty free space and \({d}_{e}\) the space density just at the surface of planet.
From "Photons Matter"
\({v}^{2}_{t}+{v}^{2}_{s} = A-B{d}_{s}(x)\)
as \(x\rightarrow \infty\), \(B{d}_{s}(x)\rightarrow B{d}_{n}\), and \(A-B{d}_{n}={c}^{2}\)
We have,
\({v}_{s}\cfrac{d{v}_{s}}{dx}-\cfrac{d{v}_{s}}{dt}=-\cfrac{B}{2}\cfrac{d{f}_{s}(x)}{dx}\)
where \({f}_{s}(x) ={ e }^{ -\cfrac { x}{ r } }({ d }_{ e }{ -d }_{ n })\),
\({v}_{s}\cfrac{d{v}_{s}}{dx}-\cfrac{d{v}_{s}}{dt}=\cfrac{B({ d }_{ e }{ -d }_{ n })}{2r}{ e }^{ -\cfrac { x }{ r } }\)
Once again we have,
\(\cfrac{d{v}_{s}}{dt} = 0\)
since there is no time dependence on the R.H.S; which means \({v}_{s}\) is optimal in time, ie an extreme point in time.
\({v}_{s}\cfrac{d{v}_{s}}{dx}=\cfrac{B({ d }_{ e }{ -d }_{ n })}{2r}{ e }^{ -\cfrac { x }{ r } }\)
\(\cfrac{d{v}^{2}_{s}}{dx} = \cfrac{B({ d }_{ e }{ -d }_{ n })}{r}{ e }^{ -\cfrac { x }{ r } }\)
Integrating both sides,
\({v}^{2}_{s} = C-B({ d }_{ e }{ -d }_{ n }){ e }^{ -\cfrac { x }{ r } }\)
We know that at \(x\rightarrow\infty\), \({v}_{s}\) = \(c\)
\(C\) = \({c}^{2}\)
and when \(x\)= 0, \({v}_{s}\) = \(\cfrac{c}{{n}_{e}}\) where \({n}_{e}\) is the refractive index of compressed space on the surface of earth.
\(\cfrac{c^2}{{n}^{2}_{e}}= {c}^{2}-B({ d }_{ e }{ -d }_{ n })\)
\(B({ d }_{ e }{ -d }_{ n })={c}^{2}(1-\cfrac{1}{{n}^{2}_{e}})\)
So,
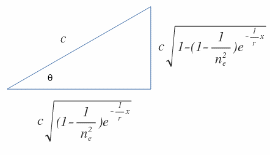
\({v}^{2}_{s} ={c}^{2}[1-(1-\cfrac{1}{{n}^{2}_{e}}){ e }^{ -\cfrac { x }{ r } }]\)
\({v}_{s} ={c}\sqrt{1-(1-\cfrac{1}{{n}^{2}_{e}}){ e }^{ -\cfrac { x }{ r } }}\)
and so,
\({v}_{t}={c}\sqrt{(1-\cfrac{1}{{n}^{2}_{e}}){ e }^{ -\cfrac { x }{ r } }}\)
Photon does not experience time while travelling at light speed, at light speed its time speed is zero. On slowing down it begins to experience time, time speed increases from zero. This is "time experience" from the other end of the spectrum. At our end, speed is slow and when approaching light speed, time speed slow from light speed and time dilates. We see from the equations that for a photon when \(x\rightarrow\infty\), \({v}_{s}\) = \(c\) and \({v}_{t}\) = 0.
Everything that we can experience have the same time speed as us. If a body has greater time speed it will speed ahead in time and disappear from our presence and if a body has a slower time speed it will also disappear, as we speed through time.
When a photon re-gain speed moving out of a gravitational field, its time speed slowed, and the photon disappears from our presence. Which explains why the night sky is dark, photons actually disappeared. When photons are completely in free space its time speed is zero. So, there're plenty of photons parked in the time dimension.
We do not experience photon until it is slowed in space and its time speed is light speed. As with all things in nature, it is likely that we detect photons (for that matter everything else) over a range of time speed. So, illumination is the process of slowing photons down. Color could then be a manifestation of different time speeds, or equivalently, how much have the photons been slowed from light speed, ie. a change in kinetic energy.
Why is time speed at light speed? The simple answer is, we will not know of speed other than time speed at light speed. If a body has greater than light speed, zero or even negative time speed, its presence is felt only when its time speed is increased to light speed, the same as us. It is not that there is no speed greater than light speed but our inability to detect speed beyond a narrow spectrum of existence around light speed in time. (There is of course anti-aliasing from varying under-sampling rate to detect consistent presence above sampling speed.) This is so, assuming that any interaction occurs over time and so all bodies involved must have the same time speed, at least momentarily.
If we formulate the time dilation equation for a photon,
\(\cfrac{{v}_{t}}{ c}=\gamma (x)=\sqrt{(1-\cfrac{1}{{n}^{2}_{e}}){ e }^{ -\cfrac { x }{ r } }}\)
This is "time experience" from time speed increasing from zero. This "time experience" is different from our time dilation when time slow from light speed. However, \({v}_{s}\) dropping from light speed is analogous to our time speed decreasing from light speed.
\(\cfrac{{v}_{s}}{ c } =\gamma (x)=\sqrt{1-(1-\cfrac{1}{{n}^{2}_{e}}){ e }^{ -\cfrac { x }{ r } }}\)
If we compare the last expression with that previously obtained,
\(\sqrt{1-(1-\cfrac{1}{{n}^{2}_{e}}){ e }^{ -\cfrac { x }{ r } }}= \sqrt{1-\cfrac{2{G}_{o}}{{c}^{2}{r}}{e}^{-\cfrac{{g}_{o}{r}}{{G}_{o}}x}}\)
We know that,
\(\cfrac{2{G}_{o}}{{c}^{2}{r}}=\cfrac{{r}_{eo}}{r}\)
and
\(\cfrac{{g}_{o}{r}}{{G}_{o}}=\cfrac{1}{r}\)
We have, at \(x\) = 0
\(1-(1-\cfrac{1}{{n}^{2}_{e}}) = 1-\cfrac{{r}_{eo}}{r}\)
\({n}_{e}= \sqrt{\cfrac{r}{r-{r}_{eo}}}\)
This expression allows the theory thus far to be checked experimentally. \({r}_{eo}\) is not a constant but specific to a planet of given mass. It was derive from considering the case when time speed on the planet is zero; what would the radius of such a planet be given mass. It was as if the planet is squeezed to greater mass density so that the space density around it is so dense that time stopped. It also correspond to the radius of a planet with an escape velocity of light speed, given planet mass, and the radius of a black hole given mass.
More importantly the time dilation factor on the surface of such a planet is given by,
\(\gamma =\sqrt{1-(1-\cfrac{1}{{n}^{2}_{e}})}\), when \(x\) = 0
\(\gamma =\cfrac{1}{{n}_{e}}\)
where \({n}_{e}\) is the refractive index on the surface of the planet. A photon experience time dilation differently, the calculation of \(\gamma\) using refractive index must be checked experimentally.