More Whacko, Jacko

From the post "The Whacko Part",

\(|B|=\cfrac{1}{4\pi \varepsilon_o }.\cfrac{q}{a^3}\)

If we consider the superposition of many moving charges,

\(B=\sum^{all-vectors}_i{\cfrac{1}{4\pi \varepsilon_o }.\cfrac{q_i}{a^3_i}}\)

The effects of moving charges before and after the point in consideration is zero.  \(B\) is entirely due to a thin sheet of charges immediately below that point, at the foot of the normal, \(n\).

\(B=\cfrac{1}{4\pi \varepsilon_o }.\sum^{all-vectors}_i\cfrac{{q_{sheet_i}}}{{a^3}}\)

If \(a\) is large,

\(B=\cfrac{1}{4\pi \varepsilon_o }.\cfrac{1}{{a^3}}\sum^{all}_i{q_{sheet_i}}\)

This sheet of charge \(J_A\) is given by,

\(J_A=\sum^{all}_i{q_{sheet_i}}=\cfrac{I}{v}\)

where \(I\) is the current and \(v\) is the average velocity of the charges.  \(J_A\) would be the current density.  This expression for \(J_A\) is also valid for conductors where the charges runs on the surface.  The B-field is then given by,

\(B=\cfrac{1}{4\pi \varepsilon_o }.\cfrac{1}{{a^3}}.\cfrac{I}{v}\)

The \({1}/{a^3}\) dependence is at odd with Ampere's Law for B-field around a current carrying wire which has a \(\frac{1}{a}\) factor.

For the normal \(E_{pn}\) component, using similar simplifications,

\(E_{pn} =B.a=\cfrac{1}{4\pi \varepsilon_o }.\cfrac{1}{{a^2}}.\cfrac{I}{v}\)

This means, if Hall Effect were used to obtain \(B\) we would find \(E_{pn}\) has a \(1/a^2\) dependence,  assuming that the dipole model for free charge is right, that \(E_{pn}\) is responsible for Hall Effect.

Hall Effect

From the previous post \(B\) generated by a moving charge/dipole, has a \(E\) component perpendicular to its direction along the perpendicular to the axis of of travel of the charge/dipole.  This normal component is given by,

\(E_{pn} = \cfrac{q}{4\pi \varepsilon_o (a^2+r^2-2a.r.cos{(\theta)})}.sin{(\theta)}\)

where \(a\) is the perpendicular distance to the axis of travel, \(q\) is the negative charge of the dipole, \(r\) is the radius of the circular path on which the negative charge is rotating and \(\theta\) is the location of the negative charge on the circular path.

Since,

\(sin(\theta)=\cfrac{R}{a}=\cfrac{\sqrt{(a^2+r^2-2a.r.cos{(\theta)})}}{a}\)

\(\therefore E_{pn} = \cfrac{q}{4\pi \varepsilon_o.a.\sqrt{(a^2+r^2-2a.r.cos{(\theta)})}}\)

when r is small,

\(E_{pn} = \cfrac{q}{4\pi \varepsilon_o.a^2}=B.a\),   since \(B=\cfrac{1}{4\pi \varepsilon_o }.\cfrac{q}{a^3}\)

It seem that \(E_{pn}\) has a bigger effect that \(B\).

For a conductor placed perpendicular to the B-field, this normal E-field component \(E_{pn}\) acts across the conductor producing a voltage difference across the surface of the conductor.  \(E_{pn}\) could be responsible for Hall Effect.

The Whacko Part

In the previous derivation \(B\) and \(E\) are in the plane perpendicular to the direction of travel, and in the case of a free charge/dipole.

\(B=-i\cfrac{\partial E}{\partial x^{'}}\)

For \(E_p\) at a distance \(a\) from the center of the circle,  The distance \(R\) from the negative charge at an angle \(\theta\) on the circumference of the circular path of radius \(r\),

\(R^2 =a^2+r^2-2a.r.cos{(\theta)}\)

and

\(E_p = \cfrac{q}{4\pi \varepsilon_o R^2}\),    so

\(E_p = \cfrac{q}{4\pi \varepsilon_o (a^2+r^2-2a.r.cos{(\theta)})}\)

\(E_p = \cfrac{q}{4\pi \varepsilon_o (a^2+r^2-2a.r.cos{(\omega.t)})}\)

where both \(a\) and \(r\) are constants and \(\theta = \omega.t\) where \(\omega\) is the angular velocity of the negative charge.

Consider, the tangential and normal component of \(E_p\),

\(E_{pt} = \cfrac{q}{4\pi \varepsilon_o (a^2+r^2-2a.r.cos{(\theta)})}.cos{(\theta)}\)

\(E_{pn} = \cfrac{q}{4\pi \varepsilon_o (a^2+r^2-2a.r.cos{(\theta)})}.sin{(\theta)}\)

For \(\theta\) very small,

\(\triangle x^{'}= Rcos{(\theta)}=cos(\theta)\sqrt{a^2+r^2-2a.r.cos{(\theta)}}\)

 \(\cfrac{\partial \theta}{\partial x^{'}}=-\cfrac{\sqrt { { a }^{ 2 }+{ r }^{ 2 }-2a.r.cos(\theta) }}{sin(\theta )(({ a }^{ 2 }+{ r }^{ 2 })-3a.r.{ cos }(\theta ))}\)

Therefore,

\(|B|=\cfrac{\partial E}{\partial x^{'}}=\cfrac{\partial E}{\partial \theta}\cfrac{\partial \theta}{\partial x^{'}}=\cfrac{\partial E_{pt}}{\partial \theta}\cfrac{\partial \theta}{\partial x^{'}}\)

Since the normal component does not effect the \(x^{'}\) direction.

\(\cfrac{\partial E_{pt}}{\partial \theta}=-\cfrac{({ a }^{ 2 }+{ r }^{ 2 })sin(\theta)}{({ a }^{ 2 }+{ r }^{ 2 }-2a.r.cos(\theta))^{ 2 }}.\cfrac{q}{4\pi \varepsilon_o}\)

\(|B|=-\cfrac{({ a }^{ 2 }+{ r }^{ 2 })sin(\theta)}{({ a }^{ 2 }+{ r }^{ 2 }-2a.r.cos(\theta))^{ 2 }}*-\cfrac{\sqrt { { a }^{ 2 }-2a.r.cos(\theta)+{ r }^{ 2 } }}{sin(\theta )(({ a }^{ 2 }+{ r }^{ 2 })-3a.r.{ cos }(\theta ))}.\cfrac{q}{4\pi \varepsilon_o}\)

\(|B|=\cfrac{({ a }^{ 2 }+{ r }^{ 2 })}{({ a }^{ 2 }+{ r }^{ 2 }-2a.r.cos(\theta))^{ 3/2 }}*\cfrac{1}{(({ a }^{ 2 }+{ r }^{ 2 })-3a.r.{ cos }(\theta ))}.\cfrac{q}{4\pi \varepsilon_o}\)

If we define \(R_s=\cfrac{a.r}{{ a }^{ 2 }+{ r }^{ 2 }}\)

\(|B|=\cfrac{q}{4\pi \varepsilon_o ({ a }^{ 2 }+{ r }^{ 2 })^{3/2}}*\cfrac{1}{(1-2.R_s.cos(\theta))^{ 3/2 }}*\cfrac{1}{(1-3.R_s.{ cos }(\theta ))}\)

When \(r\) is small compared to \(a\),  \(a\) is also the perpendicular distance to the axis of travel,

\(|B|=\cfrac{1}{4\pi \varepsilon_o }.\cfrac{q}{a^3}=\cfrac{1}{4\pi \varepsilon_o }.q/a^3\)

At this point, we know that \(B\) curves around the direction of the moving charge but Gauss's Equation in either integral or differntial form, gives no indication of this fact.  Compare this expression with Ampere's Law for B-field around a current carrying wire,  we understand why current density, \(J\) was defined and used.

Whacko and the Free Photons

I don't have Guass's Equations but, for a charge/dipole in motion,

\(B=-i\cfrac{\partial E}{\partial x^{'}}\)

the negative sign is the result of \(E\) pointing towards the negative charge in circular motion.  And the complex imaginary \(i\) is the result of rotation \(\cfrac{\pi}{2}\) anti-clockwise.  And \(x^{'}\) is in the plane perpendicular to direction \(x\)

In case of photons in motion,

\(B= i\cfrac{\partial E}{\partial x^{'}}\)

These equations prove one thing,  I am a complete WHACKO.  Because,

\(B=i\cfrac { \partial E }{ \partial x^{'} } \)

\( \cfrac { \partial B }{ \partial t } =i\cfrac { \partial ^{ 2 }E }{ \partial x^{'}\partial t } \)

\( \cfrac { \partial B }{ \partial t } =i\cfrac { \partial ^{ 2 }E }{ \partial x^{'} \partial x^{'}}\cfrac{\partial x^{'}}{\partial t } \)

Since substituting for \(B\) again,

 \(i\cfrac { \partial  }{ \partial t } \cfrac { \partial E }{ \partial x^{'} } =i\cfrac { \partial ^{ 2 }E }{ {\partial x^{'}}^{ 2 } } \cfrac{\partial x^{'}}{\partial t }\)

Multiplying both sides by \(i\) rotates both \(B\) and \(E\) again by \(\cfrac{\pi}{2}\) anti-clockwise, into the direction of \(x\), ie \(x^{'} \rightarrow x\),

 \(-\cfrac { \partial  }{ \partial t } \cfrac { \partial E }{ \partial x } =-\cfrac { \partial ^{ 2 }E }{ {\partial x}^{ 2 } } \cfrac{\partial x}{\partial t }\)

since \(\cfrac{\partial x}{\partial t } = c\)

\(\cfrac { \partial ^{ 2 }E }{ \partial t  \partial t } \cfrac { \partial t }{ \partial x } =\cfrac { \partial ^{ 2 }E }{ \partial x^{ 2 } } c\)

\( \cfrac { \partial ^{ 2 }E }{ \partial t^{ 2 } } \cfrac { 1 }{ c } =\cfrac { \partial ^{ 2 }E }{ \partial x^{ 2 } } c\)

\( \cfrac { \partial ^{ 2 }E }{ \partial t^{ 2 } } =\cfrac { \partial ^{ 2 }E }{ \partial x^{ 2 } } c^{ 2 }\)

Which is the wave equation for photons at speed \(c\).  This wave equation was derived from one relationship between \(B\) and \(E\),  this suggest that a dipole with one end spinning is all that is required for wave propagation.   In this case of a photon, the positive end is in circular motion behind the negative charge, both moving against a E-field.  Furthermore, for the case of charge/dipole

\(B=-i\cfrac { \partial E }{ \partial x^{'} } \)

\( -\cfrac { \partial B }{ \partial t } =i\cfrac { \partial ^{ 2 }E }{ \partial x^{'}\partial t } \)

\( -\cfrac { \partial B }{ \partial t } =i\cfrac { \partial ^{ 2 }E }{ \partial x^{'} \partial x^{'}}\cfrac{\partial x^{'}}{\partial t } \)

Substituting for \(B\) again,

 \(-i\cfrac { \partial  }{ \partial t }(- \cfrac { \partial E }{ \partial x^{'} }) =i\cfrac { \partial ^{ 2 }E }{ {\partial x^{'}}^{ 2 } } \cfrac{\partial x^{'}}{\partial t }\)

 \(i\cfrac { \partial  }{ \partial t } \cfrac { \partial E }{ \partial x^{'} } =i\cfrac { \partial ^{ 2 }E }{ {\partial x^{'}}^{ 2 } } \cfrac{\partial x^{'}}{\partial t }\)

Multiplying both sides by \(i\) rotates both \(B\) and \(E\) again by \(\cfrac{\pi}{2}\) anti-clockwise, into the direction of \(x\), ie \(x^{'} \rightarrow x\) and since \(\cfrac{\partial x}{\partial t }=v\)

\(\cfrac { \partial ^{ 2 }E }{ \partial t  \partial t } \cfrac { \partial t }{ \partial x } =\cfrac { \partial ^{ 2 }E }{ \partial x^{ 2 } } v\)

\( \cfrac { \partial ^{ 2 }E }{ \partial t^{ 2 } } \cfrac { 1 }{ v } =\cfrac { \partial ^{ 2 }E }{ \partial x^{ 2 } } v\)

\( \cfrac { \partial ^{ 2 }E }{ \partial t^{ 2 } } =\cfrac { \partial ^{ 2 }E }{ \partial x^{ 2 } } v^{ 2 }\)

This is the wave equation for electromagnetic wave at speed \(v\).  In this case, the negative end of the dipole is in circular motion behind the positive charge,  both moving in the direction of the E field.  The initial negative sign cancels when \(B\) is substituted again into the derivation.  The negative sign, however indicates that 

\(B=-i\cfrac{\partial E}{\partial x}\)

obeys Lenz's Law, that work is done against the change taking place; that electromagnetic wave established between two point requires continued energy input.  The wave disappears when power is lost.  In the case of photons

\(B= i\cfrac{\partial E}{\partial x}\)

runs away.  Photons continues to propagate after source power has been turned off.  Photons are free from the source once it leaves the source.

A light saber, create. Do, we will. Try Not!

Apply a strong E-field in the direction of a beam.  Does the light beam stop or disperse more than normal?  A light saber, create?

Ladies and Gentlemen, We Have Light Speed!

The previous post assumes that the negative end of the dipole is spinning and establishes a directional sense of the B-field.  What is interesting is to imagine the positive end spinning.

E field in this case is in the negative \(x\) direction.  The positive charge, in a spin, exert less pull on the negative charge than the applied E-field.  The dipole is moving right. And the B field so created is, by the right hand rule,

where y is in the clockwise sense. The first thing to notice is that the direction of E-field and B-field is consistent with that of electromagnetic wave, where \(E \times B\) = direction of wave propagation.  However,  this setup violates Lenz's Law.  The E-field cuts the B-field as the charge moves, produces a force by the left hand rule, that is in the same direction as the direction of travel of the positive charge.  That means the charge is accelerated further in the same direction.

This may be the situation we are looking for in which photons achieve light speed.  This is a consistent picture of photons being dipoles on helical path.  Added to the big picture is a spinning positive charge; the dipole is moving opposite to the applied E-field; and a mechanism to achieve terminal velocity, in free space, light speed.

What is lacking is a light-mass positive charge.  A positron may be, of mass less than an electron, to form a dipole with a heavier-mass negative charge.  That would be a marriage of light and magic.

What if?? And More What Ifs...Tadpoles

What if positive and negative charges are two manifestations of one underlying embodiment.  The surface property of some materials causes one property to show and not the other.  What if all free charges are dipoles; this includes free charges in a conductor or semiconductor.

On some material the positive end sticks out and the material is detected as positively charged, on other materials, the negative end sticks out and it is negatively charged.  One opposite the other.  In the case of conductor the negative ends of such dipoles always stick out.  Current induction as a result of moving in an electric field and force effects moving in an magnetic field are all effects on such dipoles with the negative ends just on the surface of the conductor.

This might explain why a current carrying wire is still neutral and does not exert a E-field.  That current carrying effects are just skin deep.

What if??  And more what ifs...

When subjected to a electric field in free space, the dipole move with the tail end spinning in a direction perpendicular to the direction of travel.  This spin gives raise to the B-field detected in a moving charge.  Geometry of the dipole decides the direction of spin and is consistent with the right hand rule.  The dipole now shaped like a cone move through free space or along the surface of a conductor alike.  The negative charge spin give raise to a consistent B-field.

The resultant force that provides for circular motion is pictured as such.  The E-field is in the x direction.

The definition of a dipole moment of 2 opposite charges (\(-q\),  \(+q\))  at a \(2a\) distance apart is given by

\(p=2aq\)    in the direction \(-q\) to \(+q\)

Notice that \(a\) can go infinite and we have a infinite dipole moment.  But at an infinite distance the two charges are more likely to act independently than as a dipole pair.  A more consistent view is that a force pulls the charges together when it is subject to a E-field pulling the charges apart.  Similarly a force pushes the charges apart when the charges are compressed.  This is the same force that prevents the charges from collapsing in the first place.  Let this force \({F}_{d}\) be,

\({F}_{d}=-{k}_{d}{\triangle a}\)  where \({k}_{d}\) is a constant of proportionality.

This is the simplest case of a structural restraining force.  Then, if the applied E-field is \(E\),

 \({F}_{nc}={F}_{d}sin{(\theta)}\)

This would then account for the centripetal force that give raise to spin on the negative charge.

Let examine forces on the positive charge.  There is a net force in the \(x\) direction because the spinning charge, like a ring of charges, has a lesser E-field along the line joining the center of the circular motion and the other charge.  The actual E-field as a result of this spinning charge is just that of a charged ring and is given by,

\(E_r=\cfrac{q}{4\pi\epsilon_{o}}\cfrac{x}{(x^{2}+r^{2})^{3/2}}<\cfrac{q}{4\pi\epsilon_{o}}\cfrac{1}{x^2}\)

and

\({E}_{p}=\cfrac{q}{4\pi\epsilon_{o}}\cfrac{1}{x^2}\)

A plot of 1/x^2 in red and x/(x^2+(a)^2)^(3/2) where a range from 0.001 to 1 in steps of 0.01 in blue shows that \({E}_{r}\) < \({E}_{p}\) because of \(r\).



A dipole with its tail end spinning is different from a simple dipole orientated in the direction of the a E-field.

Since \({E}_{p}>{E}_{r}\)  there is a net force in the \(x\) direction.

\({E}_{nx}={F}_{d}cos{(\theta)}+{E}_{p}-q.E\) for the \(-q\),    and

\({E}_{px}=q.E-{E}_{r}-{F}_{d}cos{(\theta)}\) for \(+q\)

These forces are such that both ends of the dipole are accelerating in the x direction with the same acceleration.

There is one other force component on \(+q\),

\({F}_{pc}={F}_{d}cos{(\theta)}\),

It is proposed that the positive charge is more massive, that this force produces a circular motion of small radius, that the positive charge is spinning along the x-axis as a first approximation.  Note: when the dipole is not subjected to an E-field, \({F}_{d}\) = 0.  \({F}_{d}\) in this case pulls the dipole together under the action of the applied E-field.

The same B-field disappears when the dipole charges stop spinning about the axis of travel or stop travelling altogether.  Such a setup would imply that B-field is actually the moving perpendicular end of an E-field.  The y direction below is in the clockwise direction perpendicular to the x direction.

To fully define the direction of the B-field in 3-D, the movement direction \(x\) and the E-field direction must all be consistent with:

1.   The right hand screw that indicate that B-field curl around a current carrying wire in the x direction.

2.    The right hand rule to find induced current in a wire cutting the B-field moving in the x direction

2.    The left hand rule that indicates an opposing force from a current carrying wire cutting through a magnetic field.

The movement direction \(x\) is always perpendicular to the E-field direction. Without the movement direction \(x\) (to indicate the direction of a force or a current), the B-field can be rotated such that the E-field points in the opposite direction and such a configuration will not be consistent, and Lenz's law will be violated.

In this model, the B-field can be replaced with a moving E-field orientated as show after considering the original B-field direction AND the direction of motion (of a force, electric current or positive charges).  The E-field is moving in the direction of  the B-field.

A stubborn Mule

If \(\varepsilon\) is a boundary effect then so should be \(\mu\).  But \(\varepsilon\) is NOT equal to \(\mu\).  Does the presence of background charges resists the establishment of a B field?  May be that is why \(\varepsilon \neq \mu\).

Fat Electrons and the Learned Inverse Square

Areas of two concentric spheres of radii \({R}_{1}\) and \({R}_{2}\),

 \(Area_1 = 4\pi {R}^2_{1}\)

\(Area_2 = 4 \pi {R}^2_{2}\)

If we consider flux emanating from a constant source of \(W\), then

\(flux_{R1} = \cfrac{W}{4\pi {R}^2_{1}}\)

\(flux_{R2} = \cfrac{W}{4\pi {R}^2_{2}}\)

from which we have the inverse square law.

\(flux  \propto  \cfrac{1}{{R}^{2}}\)

However, if

\(W \propto \cfrac{4}{3}\pi R^3 \)

where the volume immediately below is of concern, like space density, then

\(flux \propto \cfrac{ R}{3}\) as in the case of dielectric in electrostatic.

This is the case when electrons are trapped in a oil drop, a dielectric.  The factor of \(\cfrac{1}{3}\) is serious.  The term \(R\) may cancel in the final formulation, especially if the same droplet is swinging about, but the factor \(\cfrac{1}{3}\) does not go away no matter how you orientate the E flux.

This is how the fat electrons slimmed down.

Charge Kinetic Energy

\(QKE = \cfrac{1}{2}q.{v}^{2}_{q}\)

Charge kinetic energy,  an kinetic energy concept associated with the speed gained via the charge property.  If the per unit charge idea is in-cooperated we have,

\(QKE = \cfrac{1}{2}{v}^{2}_{q}\)

and by itself suggests that it does not matter how kinetic energy is gain, all of which is energy associated with motion in space.  However, the force associated with bringing such charge to motion is not \(F=ma\), instead,

\(F_c=q.a\)

where \(q\) is the charge property and \(a\) the acceleration in space.  It is a force developed by virtue of the charge property alone.   The basis of such a concept is not new, because we already have

\(E=-\cfrac{dV}{dt}\)

where E is force per unit charge.

If we skip forward all the analogy, we have the concept of time speed, \({v}_{tc}\) associated with charge ; that time is not singular but,

\({v}_{tc}^2+{v}_{tg}^2={v}_{t}^2\)

This is also not new; the idea that two effects affecting a certain parameter independently, the resultant change is not the linear sum of the individual effects but a squared sum.   A fact derived from conservation of energy of the system.  \({v}_{tg}\) is time speed associated gravity and space mass density alone.

What is important are the questions,

Does a light beam bend around a strongly charged body?  Does it bend in the same way irrespective of the sign of the charge on the body?  That both positively charged and negative charged body bend light away from its surface?

After this things get interesting...This means charges injected onto a mini black hole serve more than keeping it open, it also contribute to time dilation.

Clarice and a Beetle's Electra

One of two minds.
It covets the other, dissimilar.
Repulse one of the same.
At a distant without touching.
As if calling out by name.
How do you know thy foe?
Your greatest enemy is you?

And that not of your nature you love.
How would you know your love, without knowing you?
As simply be?...One of the other complement...which is which?
Friend or foe!

You have a partner in crime.
A whisperer, one who tells, you your nature.
And since knowing is all there is, you have within you, your opposite.

And what of this other, ... B field?
A manifestation of your opposite within?
At ninety degrees!   Not quite your opposite.
Keeping your enemy closer?  Unwise.
He tells on you.

Rocket Science

To really understand that gravity is acceleration, consider a rocket being launched.  The rocket experience huge acceleration upwards.  How is it unstable?  Its tail end tends to swing upwards, the top tip of the rocket sway from the vertical and it will rotating all the way.  Until it self-destructs.  Under gravity alone, a low C.G is stable, nothing topples over.  In high acceleration upward, the rocket will also topple - upwards!  A stable C.G is a high C.G, such that the tail end do not flip up.  A Rocket accelerating towards the heavens is as if gravity is upwards, a stable C.G is a high C.G.

Do they cancel?

Point two beams derived from the same source at each other, change the phase of one and see if they cancel.  If they do cancel then they are waves in a medium displacing the medium as they travel.  If they do not cancel then they are particle beams.

Water is H₂O particles.  Plenty of waves.

Space is a light medium, the double slit experiment was misinterpreted.  Slow electrons was "made to interfere" in a double slit setup.  Space itself squeeze through the double slit and forms the channels patterns.  Only low momentum particles are channeled and spread as interference patterns on screen.  Fast electrons break through everywhere and do not form interference patterns.  Slow electrons stay within the space channels, at least for short distances to the screen and so form up interference patterns.

Gravity has an reverse effect on photons; pushes them away.  On earth, photons tend to float up.

不舍流云消带彩
恋夕回请尽艳过
莫怨红颜早离逝
留影心怀永不老  《云夕》

I know where the \(\frac{1}{2\pi}\) factor is from.

For light,

\(c=\lambda.f\)

For photon in circular motion,

\(v=c=r\omega=r.2\pi.f\)

so,

\(\lambda = 2\pi .r\)

which is very odd indeed, because \(\lambda\) is straight \(2\pi.r\) raps around the straight line.  It is possible because the two paths do not start at the same point and do not end at the same point.  In fact the two paths do not cross ever.  It is possible when

\(r=\cfrac{\lambda}{2\pi}\)

This relationship between \(r\) and \(\lambda\) makes it easy to obtain \(r\).  All calculations involving \(r\) can be replaced with \(\frac{\lambda}{2\pi}\).

\(\hslash\), and life goes on.

Ellipse 2014

\(\triangle s\quad =\quad \sqrt { x^{ 2 }+y^{ 2 } } .\triangle \theta \)

\((\triangle s)^{ 2 }=(x^{ 2 }+y^{ 2 }).(\triangle \theta )^{ 2 }\)

\((\triangle s)^{ 2 }=(x^{ 2 }+b^{ 2 }(1-\cfrac { x^{ 2 } }{ a^{ 2 } } )).(\triangle \theta )^{ 2 }\)

\((\triangle s)^{ 2 }=({ x }^{ 2 }(1-\cfrac { b^{ 2 } }{ a^{ 2 } } )+b^{ 2 }).(\triangle \theta )^{ 2 }\)

Consider \(\cfrac { x }{ a } =cos(\theta )\)    and   \(\cfrac { y }{ b } =sin(\theta )\)

Since, \(sin^2(\theta )+ cos^2(\theta ) = 1= \cfrac { x^2 }{ a^2 }+\cfrac { y^2 }{ b^2 }\),    which is equation of the ellipse.

Substituting \(x=acos(\theta )\) into the equation for \(\triangle s\),

\((\triangle s)^{ 2 }=( a^2\cos ^{ 2 }{ \theta  }(1-\cfrac { b^{ 2 } }{ a^{ 2 } } )+b^{ 2 }).(\triangle \theta )^{ 2 }\)

\(\iint {(ds)^2}=\iint { \cos ^{ 2 }{ \theta  } ({ a }^{ 2 }-b^{ 2 })+{ b }^{ 2 } }. { (d\theta ) }^{ 2 }\)

\(\int {s(ds)}=\int {\frac{1}{2}( \theta +\sin( \theta )\cos( \theta ))({ a }^{ 2 }-b^{ 2 })+\theta{ b }^{ 2 }+A }. { d\theta }\)

\( s\cfrac { ds }{ d\theta  } =\cfrac { 1 }{ 2 } (\theta +\sin  (\theta )\cos  (\theta ))({ a }^{ 2 }-b^{ 2 })+\theta { b }^{ 2 }+A\)

When \( \theta =\pi \),\(s=0\),   so \(s\cfrac { ds }{ d\theta  }=0\)  since \(A\) is independent of \(\theta\) and not infinity (infinity is not a constant).

\(\therefore  \cfrac { 1 }{ 2 } \pi ({ a }^{ 2 }-b^{ 2 })+\pi { b }^{ 2 }+A=0\)

\( A=-\cfrac { 1 }{ 2 } \pi ({ a }^{ 2 }+b^{ 2 })\),    so

\( \int {s(ds)}=\int {\cfrac { 1 }{ 2 } (\theta +\sin  (\theta )\cos  (\theta ))({ a }^{ 2 }-b^{ 2 })+\theta { b }^{ 2 }-\cfrac { 1 }{ 2 } \pi ({ a }^{ 2 }+b^{ 2 })} { d\theta }\)

Formulating the definite integral in the positive \(x\) direction,

\( \cfrac { { s }^{ 2 } }{ 2 } =\cfrac { 1 }{ 4 } (\theta ^{ 2 }-{ \cos ^{ 2 }{ \theta  }  })({ a }^{ 2 }-b^{ 2 })+\cfrac { { \theta  }^{ 2 } }{ 2 } { b }^{ 2 }-\cfrac { 1 }{ 2 } \pi ({ a }^{ 2 }+b^{ 2 })\theta |^{ 0 }_{ \pi  }\)

\( =-\cfrac { 1 }{ 4 } (\pi ^{ 2 }-{ 1 })({ a }^{ 2 }-b^{ 2 })-\cfrac { { \pi  }^{ 2 } }{ 2 } { b }^{ 2 }+\cfrac { 1 }{ 2 } { \pi  }^{ 2 }({ a }^{ 2 }+b^{ 2 })-\cfrac { 1 }{ 4 } ({ a }^{ 2 }-b^{ 2 })\)

\( =-\cfrac { 1 }{ 4 } \pi ^{ 2 }({ a }^{ 2 }+b^{ 2 })+\cfrac { 1 }{ 2 } { \pi  }^{ 2 }({ a }^{ 2 }+b^{ 2 })\)

\( =\cfrac { 1 }{ 4 } \pi ^{ 2 }({ a }^{ 2 }+b^{ 2 })\)

\( s\quad =\cfrac { \pi  }{ \sqrt { 2 }  } \sqrt { ({ a }^{ 2 }+b^{ 2 }) } \)

\( p=2s=2\pi \sqrt { \cfrac { ({ a }^{ 2 }+b^{ 2 }) }{ 2 }  } \)

Ellipse 1986

\(\triangle s\quad =\quad \sqrt { x^{ 2 }+y^{ 2 } } .\triangle \theta \)

\((\triangle s)^{ 2 }=(x^{ 2 }+y^{ 2 }).(\triangle \theta )^{ 2 }\)

\((\triangle s)^{ 2 }=(x^{ 2 }+b^{ 2 }(1-\cfrac { x^{ 2 } }{ a^{ 2 } } )).(\triangle \theta )^{ 2 }\)

\((\triangle s)^{ 2 }=({ x }^{ 2 }(1-\cfrac { b^{ 2 } }{ a^{ 2 } } )+b^{ 2 }).(\triangle \theta )^{ 2 }\)

Consider \(\cfrac { x }{ a } =cos(\theta )\)    and   \(\cfrac { y }{ b } =sin(\theta )\)

Since, \(sin^2(\theta )+ cos^2(\theta ) = 1= \cfrac { x^2 }{ a^2 }+\cfrac { y^2 }{ b^2 }\),    which is equation of the ellipse.

Substituting \(x=acos(\theta )\) into the equation for \(\triangle s\),

\((\triangle s)^{ 2 }=( a^2\cos ^{ 2 }{ \theta  }(1-\cfrac { b^{ 2 } }{ a^{ 2 } } )+b^{ 2 }).(\triangle \theta )^{ 2 }\)

\(\iint {(ds)^2}=\iint { \cos ^{ 2 }{ \theta  } ({ a }^{ 2 }-b^{ 2 })+{ b }^{ 2 } }. { (d\theta ) }^{ 2 }\)

\(\int {s(ds)}=\int {\cfrac{1}{2}( \theta +\sin( \theta )\cos( \theta ))({ a }^{ 2 }-b^{ 2 })+\theta{ b }^{ 2 }+A }. { d\theta }\)

\( \cfrac{{ s }^{ 2 }}{2}=\cfrac { 1 }{ 4 } (\theta ^{ 2 }-{ \cos ^{ 2 }{ \theta  }  })({ a }^{ 2 }-b^{ 2 })+\cfrac { { \theta  }^{ 2 } }{ 2 } { b }^{ 2 }+A\theta |^{ \cfrac { \pi  }{ 2 }  }_{ 0 }\)

\( \cfrac{{ s }^{ 2 } }{ 2 } =\cfrac { 1 }{ 4 } (\cfrac { \pi  }{ 2 } )^{ 2 }({ a }^{ 2 }-b^{ 2 })+\cfrac { 1 }{ 2 } (\cfrac { \pi  }{ 2 } )^{ 2 }{ b }^{ 2 }+A\cfrac { \pi  }{ 2 } +\cfrac { 1 }{ 4 } ({ a }^{ 2 }-b^{ 2 })\)

\( { s }^{ 2 }=\cfrac { 1 }{ 2} (\cfrac { \pi  }{ 2 } )^{ 2 }({ a }^{ 2 }-b^{ 2 })+(\cfrac { \pi  }{ 2 } )^{ 2 }{ b }^{ 2 }+\cfrac { 1 }{ 2 } ({ a }^{ 2 }-b^{ 2 })+A\pi  \)

\(  { s }^{ 2 }=\cfrac { 1 }{ 2 } (\cfrac { \pi  }{ 2 } )^{ 2 }{ a }^{ 2 }+\cfrac { 1 }{ 2 } (\cfrac { \pi  }{ 2 } )^2{b}^{ 2 }+\cfrac { 1 }{ 2 } ({ a }^{ 2 }-{b}^{ 2 })+A\pi \)

 \(s^2=\cfrac { 1 }{ 2 } [(\cfrac { \pi  }{ 2 } )^{ 2 }{ a }^{ 2 }+(\cfrac { \pi  }{ 2 } )^2{b}^{ 2 }+({ a }^{ 2 }-b^{ 2 })+2A\pi] \)

\(s=\cfrac { 1 }{ \sqrt{2} } \sqrt { (\cfrac { \pi  }{ 2 } )^{ 2 }{ a }^{ 2 }+(\cfrac { \pi  }{ 2 } )^2{b}^{ 2 }+({ a }^{ 2 }-b^{ 2 }) +2A\pi } \)

When \(a\) = \(b\),    \(s\) = \(\cfrac{\pi}{2} a\), and swapping \(a\) and \(b\),  \(s\) should remain the same.
These conditions should solve for \(A\).

When \(a\) = \(b\),

\(s=\cfrac { 1 }{ \sqrt{2} } \sqrt { (\cfrac { \pi  }{ 2 } )^{ 2 }{ a }^{ 2 }+(\cfrac { \pi  }{ 2 } )^2{a}^{ 2 }+2A\pi } \)

\(s=\cfrac { \pi  }{ 2 } \cfrac { 1 }{ \sqrt{2} } \sqrt {2{ a }^{ 2 }+2A\pi } =\cfrac{\pi}{2}a\)

 \(\therefore 2A\pi  = 0\),   therefore, \(A\) is of the form \(B(a^n-b^n)\)

on swapping \(a\) and \(b\),

\(({ a }^{ 2 }-b^{ 2 }) +2B(a^n-b^n)\pi = ({ b }^{ 2 }-a^{ 2 }) +2B(b^n-a^n)\pi \)

\(2({ a }^{ 2 }-b^{ 2 }+2B(a^n-b^n)\pi) = 0\)

\({ a }^{ 2 }-b^{ 2 }+2B(a^{ n }-b^{ n })\pi =0\)

\( { a }^{ 2 }+2B\pi a^{ n }-(b^{ 2 }+2B\pi b^{ n })=0\)

For the non-trivial case of \(a \neq b\),  without loss of generality \(a>b\)

\( { a }^{ 2 }+2B\pi a^{ n }>(b^{ 2 }+2B\pi b^{ n })\)   and so,

\( { a }^{ 2 }+2B\pi a^{ n }=0\)    and    \(b^{ 2 }+2B\pi b^{ n }=0\)

\(2B\pi b^{ n }=-{ b }^{ 2 }\)

\( B=-\cfrac { { b }^{ 2-n } }{ 2\pi  } \)  and

\(2B\pi a^{ n }=-{ a }^{ 2 }\)

\( B=-\cfrac { { a }^{ 2-n } }{ 2\pi  }\)

This implies \(n\) = 2 and \(B=-\cfrac { 1 }{ 2\pi  }\)

\(\therefore s=\cfrac { 1 }{ \sqrt{2} } \sqrt { (\cfrac { \pi  }{ 2 } )^{ 2 }{ a }^{ 2 }+(\cfrac { \pi  }{ 2 } )^2{b}^{ 2 }}\)

\(s=\cfrac { \pi  }{ 2 \sqrt{2} } \sqrt { { a }^{ 2 }+{b}^{ 2 }}\)

For a full ellipse,

ellipse circumference = \( 4*s= 2\pi  \sqrt { \cfrac{{ a }^{ 2 }+{b}^{ 2 }}{2}}\)

Correcta, Errata, Luckily I Am A Not Nuclear Engineer da

Errata!

Important corrections!  And no, points of the same phase on the circular paths need not bisect the circular diameter.  The normal is still at an incident angle of \(\theta\) all the same.

执手无忧月圆缺
蝶恋堪知离别时
祝世情怨常共守
交杯同甘老白头  《月词》

长夕残影长
苦思愁肠苦
冥海离隔世
溢潮别离泪
心影留唏嘘
梦忆限奈河 《念苦》

单蝶倘扑风
流忆化怨水
孤蝉哀鸣隐
追悔枕潭泪
仰首落刃笑
难堪错情罪 《似水》

光子无定时
闪烁极速过
傲视凡世俗
不沾庸碌尘
黑洞当明镜
唯亮兴呈情
三问何质有
再问何匆匆  《问光》

Does Size Matter?

Does size matter?

See this quantum charge being \(\frac{1}{3}e\).  I think it is \(\frac{1}{\pi}e\).   Without the right charge, then the dipole is wrong... What the \({F}_{n}\), \(F\)?  What is the nature of electrostatic forces?  What if space is not is electrically neutral?

Is there a force on the dipole simply because physically the negative charge is smaller and the field lines are denser where they terminates on its surface?  The field line tends to space apart so there is a net force rightwards?

If space is not neutral but has a net negative charge, then dipole as a whole will experience a net force due the physical shape of the dipole.  Consider a cone with open radius  \(R_1\)  and  \(R_2\) along \(R\), an elemental surface \(ds\) on the cove surface is given by

\(ds = dp.dh\)

\(dp = R.d\phi\),   \(dh= \cfrac{{dx}}{\cos{(\theta)}}\)

\(ds =  R.d\phi.\cfrac{dx}{\cos{(\theta)}}\)

The elemental charge on the surface is,

\(dq=\sigma.ds\)     where    \(\sigma\) is the surface charge density of space around the cone.  The potential at the apex is

\(dV= \cfrac{1}{4\pi\varepsilon_o}\cfrac{\sigma.ds}{r}\)

Since,

\(r=\cfrac{x}{\cos{(\theta)}}\)     \(R=x.\tan{(\theta)}\)

\(dV=\cfrac{1}{4\pi\varepsilon_o}\sigma \tan{(\theta)}d\phi dx\)

\(x\) cancels away.

\(V = \cfrac{\sigma}{4\pi\varepsilon_o}.\tan{(\theta)}\int^{2\pi}_{0}\int^{R_2/\tan{(\theta)}}_{R_1/\tan{(\theta)}}{dx}\)

\(V = \cfrac{\sigma}{2\varepsilon_o}.\tan{(\theta)}\int^{R_2}_{R_1}{dx}\cfrac{1}{\tan{(\theta)}}\)

\(E = -\cfrac{dV}{dx}= -\cfrac{\sigma}{2\varepsilon_o}\)

There is net force on the structure through the apex along the \(x\) direction.  This might be the perpetual force on the dipole that gives it light speed.  Direction, but no magnitude to be conclusive.

Photon Mass and What the F

This post is not true. Planck's relation may not be true.  However, the first part of the Energy vs Frequency is still valid and we can restrict ourselves to interaction of the photons with the outermost electron shell.

There is another way to obtain \({m}_{p}\), consider the total energy of the photon in motion,

Total Energy = Rotational KE + Linear KE = \(h.f\)

where \(h\) is the Planck Constant, then

\(\cfrac{1}{2}{m}_{p}{c}^{2}+\cfrac{1}{2}{m}_{p}{c}^{2}\) = \(h.f\)

\(4\pi^2{m}_{p}r^2.f = h\)

\(\cfrac{4\pi^2{m}_{p}}{h}.f = \cfrac{1}{r^2}\)                        (*)

A plot of \(\cfrac{1}{r^2}\) vs \(f\) we obatin the gradient,

\(\cfrac{4\pi^2{m}_{p}}{h}\) = gradient

\({m}_{p}\) = gradient*\(\cfrac{h}{4\pi^2}\)

This may be a better way to obtain \({m}_{p}\), the photon mass.  Consider,  where the photon is in circular motion,

 \(\omega^{ 2 }=\cfrac { F }{ { m }_{ p } } \cfrac { 1 }{ r }\)

 \(\cfrac { 4{\pi}^2{ m }_{ p } }{ F }.f.\cfrac{1}{r}.f= \cfrac { 1 }{ r^2 }\)    comparing with (*) then,

\(F.r=h.f\)    and so,

\(F = \cfrac{h.f}{r}\)

This is very serious.  The dimensions in the expression check out.  Previous experimental data of \((f,r)\) pairs can be used to verify this expression and also whether the assumption \({F}_{i}=\cfrac{F_o}{{n}_{i}}\) is true.  This is also the force that drives the photon to light speed.  Why does this force exist?  If it is due to asymmetry along the dipole separation then, one geometrically big charge and the other size small may be the reason.

Not Quite Photon Mass

Consider the force on the dipole in circular motion,

\(F={m}_{p}\cfrac{c^2}{r}={m}_{p}r.\omega^2={m}_{p}r.(2\pi .f)^2\)

this is also the force driving a photon to light speed \(c\) and the drag force such that the photon is at terminal velocity.  For a given medium \(F\) is a constant.

 \(\omega^{ 2 }=\cfrac { F }{ { m }_{ p } } \cfrac { 1 }{ r }\)

 \(\log(\omega)=\cfrac { 1 }{ 2 } \log(\cfrac { F }{ { m }_{ p } } )-\cfrac { 1 }{ 2 } \log(r)\)

A plot of \(log(\omega)\) vs \(\log(r)\) can then provide a value for \(\cfrac{F}{{m}_{p}}\)

Since \(F\) is characteristic of a particular medium, we generate a number of y-intercepts \({y}_{i}\)for different mediums \({n}_{i}\).  We know that,

\(F\propto {c}^{2}\) and in a medium of refractive index \(n_i\), \({v}^2_{s}=\cfrac{{c}^{2}}{n^2_i}\)

as such,

\({F}_{i}=\cfrac{F_o}{{n}_{i}}\),  where \(F_o\) is the driving force in vacuum.

\({y}_{i} =\cfrac { 1 }{ 2 } \log(\cfrac { F_o }{ { m }_{ p } } ) - \cfrac { 1 }{ 2 }log{({n}_{i})}\)

A plot of \({y}_{i}\) vs \(log{({n}_{i})}\) will provide a value for  \(\cfrac{F_o}{{m}_{p}}\).

From the Post "Wave Front and Wave Back" , after total internal reflection,

\({r}_{c2} = \cfrac{{r}_{c1}}{cos(\theta)}.\sqrt{(\cfrac{{n}_{1}}{{n}_{2}})^2.sin^2{(\theta)}-1}\)

\({r}_{c2} = {r}_{c1}\) when

\(cos{(\theta)}=((\cfrac{n_1}{n_2})^2-1)^\cfrac{1}{2} ({(\cfrac{n_1} {n_2})^2+1})^{-\cfrac{1}{2}}\)

A diagram of total internal reflection at this angle is shown,

As the ray enters the second medium \({n}_{2}\) photons speed up tracing a longer path.  The intrusion into \({n}_{2}\) is given by \(\cfrac{2r.cos{(\theta)}}{tan{(\theta)}}\) which can be measured.  Given different frequency \(f\), \(r\) is different at the same angle of incident \(\theta\).  Hopefully the first plot can be obtained.  Repeating the measurements using different mediums \({n}_{i}\), the second plot may be obtained.  And so, \(\cfrac{F_o}{{m}_{p}}\) the photon acceleration under the driving force in free space can be approximated.

Just Lots of Colors, Retro Disco

If Planck's relation is not true this is still plausible because Planck is correct up to the first plateau of the stepped Energy vs Frequency curve.  Energy is quantized because the electrons are arranged in shells and there is no interaction between the photons and the electrons when the radius of the photon helix path is between electron shells.

From the previous post "All Creatures Great and Small", we modeled the dipole as a spring of spring constant \(k=2h\).  If we look at the expression for a dipole again,

 \({\delta E_l}=\cfrac{1}{4\pi\varepsilon_o}\cfrac{q.a}{z^3}\)

where \({\delta E_l}\) is force per unit charge then obviously the load to the model spring is a charge \(q\).

We may also see that,

\(k=2h=\cfrac{1}{4\pi\varepsilon_o}q\),   so

\(h=\cfrac{1}{8\pi\varepsilon_o}.q\)

We may have just derived Planck constant.  Just kidding, the charge on the photon dipole is,

\(q= h.8\pi\varepsilon_o\)

\(q\) = 6.62606957*10^(-34)*8*pi*8.854187817620*10^(−12) = 1.4745*10^(-43) C

A very small partial charge indeed.

Furthermore, such a spring system has a resonance,

\({f}_{reso}=\cfrac{1}{2\pi}\sqrt{\cfrac{k}{q}}=\cfrac{1}{2\pi}\sqrt{\cfrac{2h}{q}}\)

\({f}_{reso}\) = (2*6.62606957*10^(-34)/ (1.4745*10^(-43)))^(0.5)/(2*pi) = 94.803/(2.pi)= 15.088 kHz

in which case the dipole distance \(a\) increases greatly or \(\sqrt{f}\) increases greatly and since energy is proportional to frequency (Planck relation), energy of the photon increases greatly.  Death Rays!

Note:  Do not confuse \({f}_{reso}\) with \(\sqrt{f}\), the dipole distance \(a\) is made to oscillate at \({f}_{reso}\),  and begins to display wide swing,  and the photon ray shows wide color variations as \(\sqrt{f}\) changes widely.

All Creatures Great and Small

E-field of light range from 10^(-14) Wm^-2 to 10^(12) Wm^-2 .  Superposition at the detector would mean the measured value is dependent on Intensity.  Since the the dipole comes around to the the same position \(f\) times per second that means, time average over one second, the measured value is dependent on the frequency of the circular motion also.

We are looking for possibly one small value.  Let this small value be \(\delta E_l\)

According to Poynting,

From \(S= E \times H\)

\([S] = \cfrac{{E}^{2}_o}{2{Z}_{w}}\) Wm^-2

where \({Z}_{w}\) the wave impedence is \({Z}_{w}=\cfrac{{E}_{o}}{{H}_{o}}=\sqrt{\cfrac{{\mu}_{r}{\mu}_{o} }{{\varepsilon }_{r}{\varepsilon }_{o}}}\) = 376.7 \(\Omega\) for free space. So, for a photon,

\([S_p] = \cfrac{{E}^{2}_{l}}{2{Z}_{w}}\)

According to Planck,

\({E}_{n}= h.f\)

where \(h\) is the Planck constant and \(f\) the frequency of the light.  So the power of a helix of photon is given by

\(W = c.N.{E}_{n}= c.N.h.f\) Wm^-2

where \(N\) is the number of photons per unit volume (m^-3) and \(c\) light speed.

Together with Poynting formulation where N = 1 m^-3,

\(\cfrac{{{\delta E_l}^2}}{2{Z}_{w}} =c.h.f\),

since, \(c = \cfrac{1}{\sqrt{{ \varepsilon  }_{ o }{ \mu  }_{ o }}}\) and \({Z}_{w}=\sqrt{\cfrac{{\mu}_{o} }{{\varepsilon }_{o}}}\)

\({\delta E_l}^2=\cfrac{2h}{{\varepsilon }_{o}}.f\)

This is just a restatement of Planck relation.  And so,

\({\delta E_l}=\sqrt{\cfrac{2h}{{\varepsilon }_{o}}.f}\)

and correspondingly,

\({\delta H_l}=\sqrt{\cfrac{2h}{{\mu}_{o}}.f}\)

A plot of \({\delta E_l}\) over the THz range spectrum, 10^(5)*(2*6.62606957*10^(-12)*x/1.112650056)^(0.5) scaled  in the y axis by 10^(5).

Typical values are, at 430 THz is 7.156*10^(-5) Vm^-1 and at 720 THz, 9.26*10^(-5) Vm^-1. And the corresponding E-field are 9.49072*10^(-13) Wm^-2 and 1.22816*10^(-12) Wm^-2.  I have thought I can get rid of \(f\) by multiplying it to \({\delta E_l}\), as it turn out Poynting energy conservation has already in cooperated \(f\).  So, photon is not a simple dipole rotating at \(f\), along a helix.  This dipole is being stretched at higher frequency.  In this treatment, \({\delta E_l}\) is just \({E}_{o}\) of a electromagnetic wave going on at light speed \(c\) and \(\omega\) = \(2\pi f\).

If we just consider the distance \(a\) between the charges in a dipole,  \({\delta E_l}=\cfrac{1}{4\pi\varepsilon_o}\cfrac{q.a}{z^3}\)

\(\cfrac{a_1}{a_2} = \sqrt{\cfrac{{f}_{1}}{{f}_{2}}}\),    or

\(\cfrac{a^2_1}{a^2_2} = \cfrac{{f}_{1}}{{f}_{2}}\)

since according to Planck, frequency is proportional to energy via Planck constant, \(h\),

 \({E}_{n} = h.f=\cfrac{k}{2}a^2\),    where \(\cfrac{k}{2}\) mimic a spring.

This suggest that the dipole can be model as a spring of stretch length \(a=\sqrt{f}\) and spring constant \(k=2h\).

The Shiny Moon is a Black hole

At the Moon's core is a black hole.  The gravity of this black hole attracts and holds the material on the Moon.  More Importantly,  light find its way into the core and is reflected back into space with a time lag.  That is why the Moon is shiny in the night.  The different phases of the Moon we see, is not the immediate shadow of Earth but after some time delay.  That is why, some time we can see the crescent Moon in the morning light of dawn.  The time delay in lights being reflected from the core, may also explains the Red or Blue Moon phenomenon when the Moon is clearly of a different color from the moment Sun.

A check of the gravity due to a black hole at a Moon radius distance  of 1737 km is

(5.07071*10^18)*e^(-0.11286690*1737) = 3.645189859433215e-67 kms^-2

a zero on most calculator.  Gravity on the Moon is largely due to the material around the core and not the black hole at the core.

The Moon still reflects light from the Sun and during an lunar eclipse we see the relative differences as Earth casts a immediate shadow over the surface of the Moon.

We of course leave room for the fact that when the cow jumped over the Moon it left behind some.  Having said that,  if we drill a hole deep enough into the Moon towards its center, we will see a tunnel of light from the core.  And please, do not fuck up the Moon.  If the post "Onion Earth, What a Spin, Daily" is right, the Moon is responsible for Earth's day and night spin.

Shiny Black Hole

From the post "No Poetry for Einstein"

\(E = m{c}^{2}\) was interpreted as kinetic energy along the time dimension.

Unless photons have the same time speed as us, photons do not exist in the same way as us and its mass is to be interpreted differently.  Photons will have a time speed of \(c\) only when \({v}_{s}\) is zero in free space.  This would otherwise be called rest mass.

From the post "A Right Turn, A Wrong Turn" we have the equation for photon deceleration under gravity,

\({g}_{B} =\frac{1}{2}\cfrac{c}{r}\cfrac{1}{\sqrt{1-{ e }^{ -\cfrac { x }{  r }  }}}{ e }^{ -\cfrac { x }{  r }   }\)

and the velocity field,

\({v}_{r}(x)=c\sqrt{1-e^{-\cfrac{x}{r}} }- {v}_{or}\)

When \({v}_{or}\) is \(c\), that is light approaching directly towards the center of the black hole, on the surface of the black hole \({v}_{s}\) is zero.  At that point \({v}_{t}\) = \(c\) and photon manifest its true mass.  Thereafter still under deceleration, photon bounces out of the back hole.  BUT light cannot escape from a black hole!  

Light inside a black hole cannot escape the black hole and light outside the black hole cannot enter.  Light insight the black hole at \({v}_{s}\) = \(c\) and \({v}_{t}\) = 0 cannot escape the black hole.  Light from outside the black hole, on reaching the black hole \({v}_{s}\) = 0, \({v}_{t}\) = \(c\) can not go further but is under high deceleration and returns with increasing \({v}_{s}\).

So if you shine a light at a black hole it will reflect.  A black hole is shiny under illumination.

What the \({F}_{n}\), \(F\)?

Let's say a photon is propel forward by a force \({F}\), at terminal velocity a drag force develops that just opposes this force such that its velocity is \(c\), light speed.  However,  there are two other perpendicular degrees of freedom.  A drag force also develop along one of the two axis such that the velocity is also a constant in that direction.  At the same time a third force, acting as centripetal force \({F}_{c}\), brings the system into circular motion.  The resulting circular motion has no movement along \({F}_{c}\) and so the drag force in that direction is zero.  That means the centripetal force is the same force \(F\) that drives the photon forward.

A photon being setup

This can be true if the medium surrounding the photon is providing the propelling force, that such a force has no directional dependence.  On earth, photons bounce off region of higher gravity, that means photons are always in motion upwards.

The relationship,

\(F={m}_{p}\cfrac{c^2}{r}\)

is a precarious one.  It suggest that given a medium that provides \({F}_{n}\), and given photon mass \({m}_{p}\),

\(F_n={m}_{p}\cfrac{c^2}{n^2 .r}\)

where n is the refractive index of the medium.  Then \(r\) the radius of the circular path is fixed, at least initially.  But the post "Wave Front and Wave Back" shows that \(r\) can vary continuously with incident angle. One possibility is that \(r\) changes temporarily,  under the force \({F}_{n}\) acting as the centripetal force, \(r\) returns to the value given by the equation above.  If polarization is the result of changing \(r\), this would mean polarization is also temporary.  Along the path of the polarized beam, the beam looses its polarization.

The force in circular motion does not do work but the photons has rotation kinetic energy in addition to \(\cfrac{1}{2}{m}_{p}{c}^{2}_n\).  The photon is constantly being acted upon by a force from the medium it is in, such that it eventually reaches its terminal speed \({c}_{n}\) in the medium and resume a helix path, where \(r\) is given by the last equation.

The path of the photon is straight down the helix.  The circular plane containing the circular motion at any instance is always perpendicular to the direction of travel.  Both velocities are at light speed, \(c\) or in some medium of refractive index \(n\), \(\cfrac{c}{n}\).  So if light speed is \(c\) in free space, the photons may actually have speed greater than light speed instantaneously.

More Power, Unlimited Power... Reflected Totally Internally

From

\(|{r}_{c2}| =\cfrac{{r}_{c1}}{cos(\theta)}.\sqrt{(\cfrac{{n}_{1}}{{n}_{2}})^2.sin^2{(\theta)}-1}\)

it is possible to concentrate all energy along the direction of travel by total internal reflection off a less dense medium.  In which case, the photon is travelling along the helix in a very tight circular motion.

The equation does not suggest whether the circular motion re-emerge in the same direction or opposite.  But it is certain that the circular path of the helix is small just when the photon beam is in total internal reflection, and as the incidence angle increases the circular path radius increases,

A plot of the above equation where the y-axis has been scaled by 10\({r}_{c1}\) units with \({n}_{1}\) = 1.5 and \({n}_{2}\) = 1, and incident angle \(\theta\) in the x-axis in radians.  The actual equation plotted is 10/cos(x)*((1.5)^2*(sin(x))^2-1)^(0.5).  We see that the reflected radius is many times the incident radius.  This could be the explanation for dispersion of light after total internal reflection.  And when the light first emerges from total internal reflection its radius is close to zero,  this is when it is observed that light is polarized.  This might suggest that circular polarization refers to the photon in circular motion.  That photon not in circular motion is polarized light.

More importantly, this discussion leads to the conclusion that photon carries a electric field along the direction of travel in the circular path,  that photons are electric dipoles.  And since the photons are moving, a magnetic field develops in the perpendicular direction.

Notice that the E-field (in red) starts at a phase of \(\frac{\pi}{2}\) and a corresponding H-field (in blue).  At \(\lambda\), the wave advances by one cycle and the E-field is back to its original position.  There is no indication here how large the radius is.

Wave Front and Wave Back

The wave front theory assumes that light travels in parallel wave fronts,

Wave Transverse Vector

The parallel lines here are not wave fronts but vector lines of the velocity component that is perpendicular to the direction of travel with the same phase on the circular path.  This velocity is the circular velocity.  Such velocity are always perpendicular to the direction of travel.   There is no artificial wave front, but an assumption that in all mediums the photon travels in similar helical paths.  That means parallel lines remains parallel lines, which is the same geometrically as wave front theory but for different reason.

What is interesting is the radius of the circular path changing from medium to medium.

If the initial radius is \({r}_{c1}\) then

\({r}_{c2} ={r}_{c1}.\cfrac{cos(\phi)}{cos(\theta)}=\cfrac{{r}_{c1}}{cos(\theta)}.\sqrt{1-(\cfrac{{n}_{1}}{{n}_{2}})^2.sin^2{(\theta)}}\)

since, \(sin(\phi)=\cfrac{{n}_{1}}{{n}_{2}}sin(\theta)\).

If the photon enters from a less dense to a denser medium, \({n}_{2}\) > \({n}_{1}\)

\(\cfrac{{n}_{1}}{{n}_{2}}\) < \(1\)  \(\Longrightarrow\)  \(\phi\) < \(\theta\) for 0 < \(\phi\), \(\theta\) < \(\cfrac {\pi}{2}\)

so, \(cos(\phi)\) > \(cos(\theta)\)  \(\Longrightarrow\)  \(\cfrac{cos(\phi)}{cos(\theta)}\) > 1

that is,

\({r}_{c2}\) > \({r}_{c1}\) for all 0 < \(\theta\) < \(\cfrac {\pi}{2}\).  The circle expanded which could mean light dispersed.

In the case of the photon entering from a denser to less dense medium, \({n}_{2}\) < \({n}_{1}\),
it is possible that,

\(1-(\cfrac{{n}_{1}}{{n}_{2}})^2.sin^2{(\theta)} \) = 0

\(\theta = sin^{-1}{(\cfrac{{n}_{2}}{{n}_{1}})}\)

Which is just the case for critical angle \({\theta}_{c}\), where

\(sin(\phi)=\cfrac{{n}_{1}}{{n}_{2}}sin(\theta_c) = 1\)

 \(\phi\) = \(\cfrac{\pi}{2}\)  the refracted beam is along the inter-surface of the two mediums and has no circular component.  If energy is still conserved inside the medium then,  all energy of the photon beam is now in the direction of travel of the beam.  However,  photon speed cannot be greater than light speed.

Beyond \({\theta}_{c}\),  \({r}_{c2}\)  is complex,

\({r}_{c2} =i.\cfrac{{r}_{c1}}{cos(\theta)}.\sqrt{(\cfrac{{n}_{1}}{{n}_{2}})^2.sin^2{(\theta)}-1}\)

We know that in this case, the photon is reflected back into the denser medium,  a phenomenon called total internal reflection.

From the diagram on the right we see that,

\(sin{(\phi+\cfrac{\pi}{2})}=cos{(\phi)}=sin{(\theta^{'})}\)

This suggests that the effect of \(i\), the complex imaginary unit, rotated the frame of reference by \(\cfrac{\pi}{2}\) anti-clockwise,

 \(\phi\)  \(\rightarrow\) \(\phi+\cfrac{\pi}{2}\)  on the new reference

and the relationship

 \(sin(\phi)=\cfrac{{n}_{1}}{{n}_{2}}sin(\theta)\)

still holds, except, since both paths are in the same medium \({n}_{1}\) = \({n}_{2}\), and in the new reference frame

 \(sin{(\phi+\cfrac{\pi}{2})} =sin{(\theta^{'})}= sin{(\theta)}\),

and so,

\(\theta^{'} = \theta\)

The photon path is reflected about the surface normal with the angle of incidence equals the angle of reflection.

Uniform Medium Uniform At Large

When a photon beam enters a medium from free space, at an angle \(\alpha\) to the normal of the surface, at the point of entry,

\({v}_{sp} = v.sin{(\alpha})\),   perpendicular to the normal

\({v}_{sa} = v.cos{(\alpha})\),   along the normal

We know from previously,

\({v}^{+}_{sa} = v.cos{(\alpha)}.sin{(\theta})\)    where  \(\theta = sin^{-1}{(\cfrac{1}{n}})\)

and if both direction are equally effected by the medium,

\({v}^{+}_{sp} = v.sin{(\alpha)}.sin{(\theta})\)

The resultant direction is,

\(tan{(\beta)} = \cfrac{{v}^{+}_{sp}}{{v}^{+}_{sa} }=\cfrac{sin{(\alpha)}.sin{(\theta)}}{cos{(\alpha)}.sin{(\theta)}}=tan{(\theta)}\)

But this is not true, the path of the beam should bent inside the medium.

If \({v}_{sp}\) is not effected by the medium

\({v}^{+}_{sp} = v.sin{(\alpha)}\)

Then the new resultant direction is,

 \(tan{(\beta)} = \cfrac{sin{(\alpha)}}{cos{(\alpha)}.sin{(\theta)}} > tan{(\alpha)}\),    always

which is also not true.  In fact, from the observation that defraction is towards the normal inside a denser medium, the perpendicular velocity component is reduced more by the medium compared to the vertical component.  Since, we can rotate the beam or the medium and obtain the same results, the medium is uniform yet not.  This suggests that there is asymmetry in the plane perpendicular to the direction of the beam.  It suggests that the beam has an extend perpendicular to the direction of the beam and since the beam can be rotated, such an extend is circular in the plane perpendicular to the direction of the beam.

Either a beam of photons is not a beam of point particles, or it is a beam of point particles but the path of such point particles is not straight lines but helical; circular in the plane perpendicular to the direction of travel but straight along the length of the beam.  The latter view is consistent with the three parameters associated with light; a frequency, \(f\), where every turn of the circle perpendicular to the direction of travel move the particle forward by a wavelength, \(\lambda\) distance and so the speed \(c\) of such a beam is \(c=f\lambda\).  It might also suggests that the phase of light wave refers to the relative position of the particle in that circle.  But there are others parameter associated with a helical path: circular velocity \({v}_{c}\), radius of the circle \({r}_{c}\) projected onto a plane perpendicular to the direction of travel and the centripetal force \({f}_{c}\) giving rise to the circular motion.  The existence of a circular velocity also suggests that a beam of light has more energy than its linear speed can account for.

Photons, Bubbles and Collisons

Thinking about photons is like a fish thinking about what bubbles are and are not.

Bubbles, inside, air. Photons, inside, empty space.
Bubbles dissolve in water.  Photons dissolve in time.
Bubbles float up perpetually.  Photons at light speed.
Bubbles collide and coalesce.  Photons collide and coalesce?
Bubbles all sizes.  Photons quantized.
Bubbles has PE and KE.  Photons have KE well, \({v}^{2}_{s}\) at least,  PE?  Photons do have PE, its                                           time speed tends towards light speed.
Bubbles has mass.  Photons have mass?
Bubbles have size.  Photons have size, or just packets of energy?
Bubbles have colors.  Photons have colors?
Bubbles break up.  Photons break up?
Bubbles spin.  Photons spin?
Bubbles have momentum. Photons have momentum.
Bubbles exert a force.  Photons exert a force?
Bubbles can  be created.  Photons can be created.
Bubbles foam and stick.  Photons foam and stick?
Bubbles pair up.  Photons pair up?
Bubbles make noise.  Photons make noise, radiates?
Bubbles expand and contract.  Photons expand and contract?
Bubbles disappear.  Photons disappear.
Bubbles bounce.  Photons bounce.
Bubbles can be stored.  Photons can be stored?
Bubbles distort.  Photons distort?
Bubbles have a gravitational field around them.  Photons interact with space...
Bubbles time travel.  Photons time travel.
Bubbles block pipes.  Photons block anything?
Bubbles lense.  Photons lense?
Bubbles roll.  Photon roll?
Bubbles float up.  Photons float up in a gravitational field.
Bubbles elastic.  Photons elastic?
Bubbles get destroyed.  Photon get destroyed?
Bubbles are slippery.  Photons are slippery?
Bubbles break.  Photons break?
Bubbles chain up.  Photons chain up?
Bubbles speed reach terminal velocity.  Photons light speed, terminal velocity.
Bubbles gets bigger.  Photons expand?

Bubbles are fun...

雷雨涣晨清
独步孤道伶
雨洒伞棚急
风斜寒瑟凌
黑晕佈天远
霸影到眉近
绵力扶豆志
依符尽心勉 《又来》

In, Up, Out and Away...

From the post "A Right Turn, A Wrong Turn", the velocity component along the radial line joining the photon and the center of the planet is given by

\({v}_{r}(x)=c\sqrt{1-e^{-\cfrac{x}{r}} }\)

The perpendicular component is unaffected by gravity.  If we let an initial approach of -45 degrees at light speed,

\({v}_{op}\) = \(c.cos{\cfrac{\pi}{4}}\) = 150 scaled units

\({v}_{or}\) = \(c.sin{\cfrac{\pi}{4}}\) = -150 scaled units

Then the path of such a photon is given by,

\(\triangle S = \sqrt{({v}_{op}\triangle t)^2 +[({v}_{r}(x)+{v}_{or})\triangle t]^2 }\)

\(\triangle S = \sqrt{({v}_{op})^2 +[({v}_{r}(x)+{v}_{or})]^2 }.\triangle t\)

Integrating the above curve will involve both \(t\) and \(x\).  Instead the integration of  \({v}_{r}(x)\) is plotted on a graph, where the x-axis is traces out the path of a constant velocity component ie. a line \(y\) = \(c\) represent a velocity \(c\) in the x-axis direction and traces out a path \(c.x\), \(x\) here represent time. And the integration of a curve \(f(x)\) represent the distance traveled by the vertical velocity component spread along the x-axis, through time.  That is to say, the path of the velocity equation scaled in the x-axis which is now the time-axis also.

The actual equation plotted are, 300*(1-e^(-x/6.3))-150-225 in blue, the plot has been shifted down by 225.  The new reference axis is plotted yellow;  the integral of (300*(1-e^(-x/6.3))-150)/100 in red.

The blue curve shows that the radial velocity component of an approaching photon actually reverses direction.  The red curve shows the path of the same photon bouncing out back into space.  Where the radial velocity component is zero (yellow line and blue curve intersect) the red photon path reaches its lowest point.

Hide and Seek.. Quack.

Measure refractive index on the surface of the sphere inside which we are hiding.  The refractive index gives amount of time dilation on the sphere and also inside the sphere.  The surface of the sphere has higher space density.  We are hiding from time.

There are many ways of generating higher space density;  the cone of a sonic boom made to rotate about a disc results in a cone of higher space density; rotating blades in narrow Casimir spacing generates a layer of higher space density;  a black hole prevented from collapsing with electron charges subtends a cone of higher space density; a stream of space from rotating blades in narrow spacing has higher space density; space flow between a very hot and very cold body pushes space to one side and forms a region of higher space density; tubes in Casimir diameter acting like capillary tubes for space pushes space to one side and form regions of higher space density; a magnetic voretx; an electronic vortex; a simple lead casing of thickness 41 cm at least, and space flows around it...space is constantly moving otherwise we will not experience time.... and the list goes on as more ways are discovered.

Quack, Quack, Quack.

A Right Turn, A Wrong Turn

From the previous post "In the Limelight",

\({v}^{2}_{s} ={c}^{2}[1-(1-\cfrac{1}{{n}^{2}_{e}}){ e }^{ -\cfrac { x }{  r }  }]\)

\({v}_{s} ={c}\sqrt{1-(1-\cfrac{1}{{n}^{2}_{e}}){ e }^{ -\cfrac { x }{  r } }}\)

Which is an expression for the speed of a photon along the radial line joining the photon and the center of the planet. Given a path of light resolved into two components, one along the radial line and the other perpendicular, the radial acceleration is,

\(\cfrac{d{v}_{s}}{dx} =\cfrac{1}{2}{c}\cfrac{1}{\sqrt{1-(1-\cfrac{1}{{n}^{2}_{e}}){ e }^{ -\cfrac { 1 }{  r } x }}}(1-\cfrac{1}{{n}^{2}_{e}}).\cfrac{1}{r}{ e }^{ -\cfrac { x }{  r }  }\)

This is the expression for gravity experienced by a beam of light around a planet.  Notice that it is positive in the outward direction.  Photons actually gain speed as it leave the gravitational field of a planet.  As it approaches a planet, photon slows down, a gravitational acceleration develops that points away from the planet.  An approaching beam of light is actually deflected AWAY from a planet gravitational field.

In the case of a black hole, \({n}_{e}\rightarrow\infty\)

\({g}_{B} =\cfrac{1}{2}\cfrac{c}{r}\cfrac{1}{\sqrt{1-{ e }^{ -\cfrac { x }{  r }   }}}{ e }^{ -\cfrac { x }{  r }   }\)

And the velocity field is,

\({v}_{r}(x)=c\sqrt{1-e^{-\cfrac{x}{r}} }- {v}_{or}\)

where \({v}_{or}\) is the radial component of the initial approach velocity.  This is a field equation in \(x\), the radial distance from the planet surface outwards.  Each value of \(x\) gives a corresponding value of velocity with an outward positive value.   A sample plot of this curve (3000*(1-e^(-x/100))^(0.5)-1500) shows, that given an initial approach value, the radial velocity component of the beam eventually reverses and so is refracted away from the black hole.

The situation is just like total internal refraction where light bends away on its approach to a denser and denser medium.   The same will happen around a massive body like the Sun.  The conclusion here is however, opposite to popular believe that light bend towards the massive body.  The conclusion here is that light is refracted away from the massive body.

Note:

1.  If the beam of light is approaching at an angle \(\theta\) to the perpendicular of the radial line, then

\({v}_{or}=c.sin{\theta}\)

\({v}_{op}=c.cos{\theta}\)

where \(c\) is light speed.

In the Limelight

If we now consider a space density profile around a planet,

\( { d }_{ s }(x)={ e }^{ -\cfrac { x }{  r }  }({ d }_{ e }-{ d }_{ n })+{ d }_{ n }\)

where \(r\) is the radius of the planet, \({d}_{n}\) is a constant, the baseline space density of empty free space and  \({d}_{e}\) the space density just at the surface of planet.

From "Photons Matter"

\({v}^{2}_{t}+{v}^{2}_{s} = A-B{d}_{s}(x)\)

as \(x\rightarrow \infty\), \(B{d}_{s}(x)\rightarrow B{d}_{n}\), and \(A-B{d}_{n}={c}^{2}\)

We have,

\({v}_{s}\cfrac{d{v}_{s}}{dx}-\cfrac{d{v}_{s}}{dt}=-\cfrac{B}{2}\cfrac{d{f}_{s}(x)}{dx}\)

where \({f}_{s}(x) ={ e }^{ -\cfrac { x}{  r }   }({ d }_{ e }{ -d }_{ n })\),

\({v}_{s}\cfrac{d{v}_{s}}{dx}-\cfrac{d{v}_{s}}{dt}=\cfrac{B({ d }_{ e }{ -d }_{ n })}{2r}{ e }^{ -\cfrac { x }{  r }   }\)

Once again we have,

\(\cfrac{d{v}_{s}}{dt} = 0\)

since there is no time dependence on the R.H.S; which means \({v}_{s}\) is optimal in time, ie an extreme point in time.

\({v}_{s}\cfrac{d{v}_{s}}{dx}=\cfrac{B({ d }_{ e }{ -d }_{ n })}{2r}{ e }^{ -\cfrac { x }{  r }   }\)

\(\cfrac{d{v}^{2}_{s}}{dx} = \cfrac{B({ d }_{ e }{ -d }_{ n })}{r}{ e }^{ -\cfrac { x }{  r }   }\)

Integrating both sides,

\({v}^{2}_{s} = C-B({ d }_{ e }{ -d }_{ n }){ e }^{ -\cfrac { x }{  r }  }\)

We know that at \(x\rightarrow\infty\), \({v}_{s}\) = \(c\)

\(C\) = \({c}^{2}\)

and when \(x\)= 0, \({v}_{s}\) = \(\cfrac{c}{{n}_{e}}\) where \({n}_{e}\) is the refractive index of compressed space on the surface of earth.

\(\cfrac{c^2}{{n}^{2}_{e}}= {c}^{2}-B({ d }_{ e }{ -d }_{ n })\)

\(B({ d }_{ e }{ -d }_{ n })={c}^{2}(1-\cfrac{1}{{n}^{2}_{e}})\)

So,

\({v}^{2}_{s} ={c}^{2}[1-(1-\cfrac{1}{{n}^{2}_{e}}){ e }^{ -\cfrac { x }{  r }   }]\)

\({v}_{s} ={c}\sqrt{1-(1-\cfrac{1}{{n}^{2}_{e}}){ e }^{ -\cfrac { x }{  r }   }}\)

and so,

\({v}_{t}={c}\sqrt{(1-\cfrac{1}{{n}^{2}_{e}}){ e }^{ -\cfrac { x }{  r }   }}\)

Photon does not experience time while travelling at light speed,  at light speed its time speed is zero.  On slowing down it begins to experience time, time speed increases from zero.  This is "time experience" from the other end of the spectrum.  At our end, speed is slow and when approaching light speed, time speed slow from light speed and time dilates.  We see from the equations that for a photon when \(x\rightarrow\infty\),  \({v}_{s}\) = \(c\) and \({v}_{t}\) = 0.

Everything that we can experience have the same time speed as us.  If a body has greater time speed it will speed ahead in time and disappear from our presence and if a body has a slower time speed it will also disappear, as we speed through time.

When a photon re-gain speed moving out of a gravitational field, its time speed slowed, and the photon disappears from our presence.  Which explains why the night sky is dark, photons actually disappeared. When photons are completely in free space its time speed is zero.  So, there're plenty of photons parked in the time dimension.

We do not experience photon until it is slowed in space and its time speed is light speed.  As with all things in nature, it is likely that we detect photons (for that matter everything else) over a range of time speed.  So, illumination is the process of slowing photons down.  Color could then be a manifestation of different time speeds, or equivalently, how much have the photons been slowed from light speed, ie. a change in kinetic energy.

Why is time speed at light speed?  The simple answer is, we will not know of speed other than time speed at light speed. If a body has greater than light speed, zero or even negative time speed, its presence is felt only when its time speed is increased to light speed, the same as us.  It is not that there is no speed greater than light speed but our inability to detect speed beyond a narrow spectrum of existence around light speed in time.  (There is of course anti-aliasing from varying under-sampling rate to detect consistent presence above sampling speed.)  This is so, assuming that any interaction occurs over time and so all bodies involved must have the same time speed, at least momentarily.

If we formulate the time dilation equation for a photon,

\(\cfrac{{v}_{t}}{ c}=\gamma (x)=\sqrt{(1-\cfrac{1}{{n}^{2}_{e}}){ e }^{ -\cfrac { x }{  r }   }}\)

This is "time experience" from time speed increasing from zero.  This "time experience" is different from our time dilation when time slow from light speed.  However, \({v}_{s}\) dropping from light speed is analogous to our time speed decreasing from light speed.

\(\cfrac{{v}_{s}}{ c } =\gamma (x)=\sqrt{1-(1-\cfrac{1}{{n}^{2}_{e}}){ e }^{ -\cfrac { x }{  r }   }}\)

If we compare the last expression with that previously obtained,

\(\sqrt{1-(1-\cfrac{1}{{n}^{2}_{e}}){ e }^{ -\cfrac { x }{  r }  }}= \sqrt{1-\cfrac{2{G}_{o}}{{c}^{2}{r}}{e}^{-\cfrac{{g}_{o}{r}}{{G}_{o}}x}}\)

We know that,

\(\cfrac{2{G}_{o}}{{c}^{2}{r}}=\cfrac{{r}_{eo}}{r}\)

and

\(\cfrac{{g}_{o}{r}}{{G}_{o}}=\cfrac{1}{r}\)

We have, at \(x\) = 0

\(1-(1-\cfrac{1}{{n}^{2}_{e}}) = 1-\cfrac{{r}_{eo}}{r}\)

\({n}_{e}= \sqrt{\cfrac{r}{r-{r}_{eo}}}\) 

This expression allows the theory thus far to be checked experimentally.   \({r}_{eo}\) is not a constant but specific to a planet of given mass.  It was derive from considering the case when time speed on the planet is zero; what would the radius of such a planet be given mass. It was as if the planet is squeezed to greater mass density so that the space density around it is so dense that time stopped.  It also correspond to the radius of a planet with an escape velocity of light speed, given planet mass, and the radius of a black hole given mass.  

More importantly the time dilation factor on the surface of such a planet is given by,

\(\gamma =\sqrt{1-(1-\cfrac{1}{{n}^{2}_{e}})}\),     when \(x\) = 0

\(\gamma =\cfrac{1}{{n}_{e}}\)

where \({n}_{e}\) is the refractive index on the surface of the planet.  A photon experience time dilation differently,  the calculation of \(\gamma\) using refractive index must be checked experimentally.

Photons Really Matter

From the post "Photons Matter"

\({v}^{2}_{t}+{v}^{2}_{s} = A-B{d}_{s}(x)\)

\({v}^{2}_{t}+{v}^{2}_{s} = c^2-(c^2-\cfrac{{c}^{2}}{{n}^{2}}){d}_{s}(x)\)

And that in an uniform photon-speed-slowing medium,

\({v}_{s} =\cfrac{c}{n}.sin{\theta}\)

where \(\theta = sin^{-1}{ \sqrt{1-\cfrac{{n}_{o}}{c^2}}}\)

From the energy conservation equation,

\({v}^{2}_{t}+{v}^{2}_{s}=\cfrac{{c}^{2}}{n^2}\), if  \({v}_{s} =\cfrac{c}{n}.sin{\theta}\) then,

\({v}^{2}_{t} = \cfrac{{c}^{2}}{n^2}(1-sin^{2}{\theta}) = (\cfrac{c}{n}.cos{\theta})^2\)

\({v}_{t} = \cfrac{c}{n}.cos{\theta}\)

where \(cos{\theta}\) is given by \(\cfrac{\sqrt{{n}_{o}}}{c}\) and \({n}_{o}\) is related to the refractive index of the medium by

\({n}_{o}=c^2(1-\cfrac{1}{n^2})\)

Obviously,

\(\cfrac{{v}_{t}}{c} = \gamma =  \cfrac{1}{n}cos{\theta}=  \cfrac{1}{n}\sqrt{1-\cfrac{1}{n^2}}\)

where \(n\) is the refractive index of the medium slowing photons down.  A photon that passing through a medium that slow it down in space also experiences time dilation.  Photons begin to experience time in the denser medium.  Denser space is an optically denser medium as far as a photon is concern.

We can also formulate a complex speed expression,

\({V}_{c}= \cfrac{c}{n}(sin{\theta}+i.cos{\theta})\),    that

\({v}_{s} =Re[\cfrac{c}{n}(sin{\theta}+i.cos{\theta})]\)    and

\({v}_{t} =Im[\cfrac{c}{n}(sin{\theta}+i.cos{\theta})]\)

In other words,

\({V}_{c}= {v}_{s}+i{v}_{t}\)

where the real part is space and the imaginary part is time.  And that space and time is orthogonal.

Photons Matter

We need to know more of photons in free space to use it to understand time speed and time travel.

From the conservation of energy equation,

\({v}^{2}_{t}+{v}^{2}_{s} = {c}^{2}\)

differentiating both sides with respect to time,

\(2{v}_{t}\cfrac{d{v}_{t}}{dt}+2{v}_{s}\cfrac{d{v}_{s}}{dt} = 0\)

\({v}_{t}\cfrac{d{v}_{t}}{dx}\cfrac{dx}{dt}+{v}_{s}\cfrac{d{v}_{s}}{dt} = 0\)

\({v}_{t}\cfrac{d{v}_{t}}{dx}{v}_{s}+{v}_{s}\cfrac{d{v}_{s}}{dt} = 0\)

\({v}_{t}\cfrac{d{v}_{t}}{dx} = - \cfrac{d{v}_{s}}{dt} \)

Now consider time being terminal velocity in space and photon speed also as terminal velocity in space, both will then have an inverse proportional relationship with space density.  For a photon,

\({v}^{2}_{t}+{v}^{2}_{s} = A-B{d}_{s}(x)\)

Differentiating with respect to \(x\)

\(2{v}_{t}\cfrac{d{v}_{t}}{dx}+2{v}_{s}\cfrac{d{v}_{s}}{dx} = -B\cfrac{d{d}_{s}(x)}{dx}\)

Since, \({v}_{t}\cfrac{d{v}_{t}}{dx} = - \cfrac{d{v}_{s}}{dt} \)

\({v}_{s}\cfrac{d{v}_{s}}{dx}-\cfrac{d{v}_{s}}{dt}=-\cfrac{B}{2}\cfrac{d{d}_{s}(x)}{dx}\)

If we let \(\cfrac{d{v}_{s}}{dt} = 0\) since there is no time dependentce on the R.H.S, that is, to optimize in time; ie. for an extrema of \({v}_{s}\) in time,

\({v}_{s}\cfrac{d{v}_{s}}{dx} =-\cfrac{B}{2}\cfrac{d{d}_{s}(x)}{dx}\)

for the case of \({d}_{s}(x)\) = constant, ie a uniform medium,

\({v}_{s}\cfrac{d{v}_{s}}{dx} = 0\)

\({v}_{s}=C\) or \({v}_{s}=0\)  we are looking for non-trivial answers as such

\({v}_{s}=c\)

since we know that in uniform free space photon speed is light speed \(c\).  And in general photon speed in any uniform medium is a constant.

Then we consider a photon entering a uniform medium from free space,

\({d}_{s}(x) = \cfrac{{n}_{o}}{B}step(x)\) where the medium is modeled as a step function at \(x\) = 0,

ie, replacing \(B\) with \({n}_{o}\)

\({v}_{s}\cfrac{d{v}_{s}}{dx} =-\cfrac{{n}_{o}}{2}\cfrac{d (step(x))}{dx}\)

\(\cfrac{1}{2}\cfrac{d{v}^{2}_{s}}{dx} = -\cfrac{{n}_{o}}{2}\cfrac{d (step(x))}{dx}\)

Integrating both sides,

\({v}^{2}_{s} = C-{n}_{o}step(x)\)

We know that \({v}_{s}\) = \(c\) when \(x\) = 0^-, so when \(x\) > 0

\({v}^{2}_{s} = c^2-{n}_{o}\) where \(c\) is light speed.

So,

\({v}_{s} = \sqrt{c^2-{n}_{o}}\)

If we consider the ratio in change of speed after the photon has passed into the medium,

\({v}_{s} =c. \sqrt{1-\cfrac{{n}_{o}}{c^2}}\)

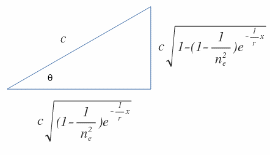
\({v}_{s} =c.sin{\theta}\)

where \(\theta = sin^{-1}{ \sqrt{1-\cfrac{{n}_{o}}{c^2}}}\)

Remember that refractive index \(n\),

\(n=\cfrac{c}{{v}_{s}}=\cfrac{1}{sin{\theta}}\) ≥ 1

This is consistent with established definition of \(n\).  There is a relationship between optical density and space density.  We see that,

 \(\theta = sin^{-1}{ \sqrt{1-\cfrac{{n}_{o}}{c^2}}}=sin^{-1}{\cfrac{1}{n}}\)

then,

\( \sqrt{1-\cfrac{{n}_{o}}{c^2}}=\cfrac{1}{n}\)

\(c^2-{n}_{o}=\cfrac{{c}^{2}}{{n}^{2}}\)

\({n}_{o}=c^2-\cfrac{{c}^{2}}{{n}^{2}}=c^2(1-\cfrac{1}{{n}^{2}})=B\)

Consider again,

\({v}^{2}_{t}+{v}^{2}_{s} = A-B{d}_{s}(x)\)

At \(x\) = 0^-   \({d}_{s}(x)\) = 0,  so \(A\) = \(c^2\).  And so at \(x\) = 0⁺

\({v}^{2}_{t}+{v}^{2}_{s} = \cfrac{{c}^{2}}{{n}^{2}}\)

where \(\cfrac{c}{n}\) is the speed of photon in a medium of refractive index \(n\).  We started with energy conservation equation,

\({v}^{2}_{t}+{v}^{2}_{s} = {c}^{2}\)

on crossing a medium boundary \({n}_{o}step(x)\), we obtained,

\({v}^{2}_{t}+{v}^{2}_{s} = \cfrac{{c}^{2}}{{n}^{2}}\)

Energy is lost, by a factor of \((1-\cfrac{1}{{n}^2})\).

We also see clearly what does least time, (ie. \(\cfrac{d{v}_{s}}{dt} = 0\)), that is, to optimize in time means;  all changes in the energy conservation expression occurs in \({v}_{s}\) only, as we set \(\cfrac{d{v}_{s}}{dt} = 0\).  This, however may not be true if we are able to track individual photons.  Under normal circumstances, we observe the behavior of many photons over time and obtain time averaged parameters.  If we are able to focus on the behavior of individual groups of photons it is likely that the change in time and space be distributed according to some distribution function.  That in time and space, the photons disperse.  From the differential equation, we have the case of \(\frac{d{v}_{s}}{dt} = 0\).