I was thinking,
\(Na\longrightarrow H\, +\, positive\,\,temp.\,\, partilces\)
and then
\( Na+H_{ 2 }O+H\longrightarrow NaOH +H_2\)
but they are at odds with basic ionic chemical equations. The idea is that more temperature particles in hydrogen (\(H\)) makes sodium (\(Na\)); as one move down a group in the periodic table. One way of releasing those positive temperature particles in sodium (Na) is to react it with water (\(H_2O\)). In the process, the metal is transmuted up the group in the period table, into hydrogen (\(H\)). Lithium (\(Li\)), is found in trace amount at the end of the reaction.
\(2Na+H_{ 2 }O\longrightarrow NaOH+H_2\, +\, positive\, \, temp.\, \, partilces\)
which combines the previous two equations. This might explain the mass discrepancy observed when the metal reacts with water.
Sodium is a positive temperature particle source.
Saturday, December 19, 2015
Wednesday, November 18, 2015
Time Force And Time Travel
When a time traveler brings a future invention and show it to the would be inventor, he triggers a time correction that is experienced as a physical force in space. Everyone associated with the invention are affected. If the invention is a popular one, used by many, this time wave is catastrophic.
When an inventor invents something new, he creates a singularity in time, an event without precedent that triggers other events. The invention is the source of many events. When the inventor is shown his future invention, the singularity in time is destroyed. He is not going to invent something shown to him, that as far as he is concerned, already exist. The series of events that flows the singularity collapse and the inventor is left with a sense of lost and a hard push.
If we imagine events in time having mass, and that a time singularity provides the motive force that drives such "event mass" to time speed (light speed) along the time dimension, destroying the singularity stops such event mass along the time dimension, onto which, we, still at time speed along the time dimension, collide. Such collisions result in a change in our moment along the time dimension.
This is postulated origin of the time wave that we experience as a force in the space dimension. In the space dimension,
\(F=m\cfrac{d^2x}{dt^{2}}\)
but \(F\ne0\) as the result of a change in \(t\), which we now denote as \(t^{'}\),
\(F=m\cfrac{d\,}{dt}\left\{\cfrac{d\,x}{dt}\right\}=m\cfrac{d\,}{dt}\left\{\cfrac{\partial\,x}{\partial t}+\cfrac{\partial\,x}{\partial t^{'}}\cfrac{dt^{'}}{dt}\right\}\)
where \(dt^{'}\) (or \(\Delta t^{'}\)) is due to the change in time speed (in us, the body that experience the time correction force in the space dimension) as a result of the collision along the time dimension with "event mass" that stopped due to the destruction of its time singularity that drove it forward originally.
We collide with "event mass" along our time line (our straight path in the time dimension). If we are not associated with the invention (that disappeared in time), then such "event mass" does not exist along our time line, in this way this time correction has a strange property that only bodies associated with the invention experience the force directly, irrespective of their location in space.
This is good, for a start to quantify such a strange force in space as a result of effects in time. Can we time travel using such a force?
Have a nice day.
Note: The biggest time singularity is the Big Bang or Creation itself.
When an inventor invents something new, he creates a singularity in time, an event without precedent that triggers other events. The invention is the source of many events. When the inventor is shown his future invention, the singularity in time is destroyed. He is not going to invent something shown to him, that as far as he is concerned, already exist. The series of events that flows the singularity collapse and the inventor is left with a sense of lost and a hard push.
If we imagine events in time having mass, and that a time singularity provides the motive force that drives such "event mass" to time speed (light speed) along the time dimension, destroying the singularity stops such event mass along the time dimension, onto which, we, still at time speed along the time dimension, collide. Such collisions result in a change in our moment along the time dimension.
This is postulated origin of the time wave that we experience as a force in the space dimension. In the space dimension,
\(F=m\cfrac{d^2x}{dt^{2}}\)
but \(F\ne0\) as the result of a change in \(t\), which we now denote as \(t^{'}\),
\(F=m\cfrac{d\,}{dt}\left\{\cfrac{d\,x}{dt}\right\}=m\cfrac{d\,}{dt}\left\{\cfrac{\partial\,x}{\partial t}+\cfrac{\partial\,x}{\partial t^{'}}\cfrac{dt^{'}}{dt}\right\}\)
where \(dt^{'}\) (or \(\Delta t^{'}\)) is due to the change in time speed (in us, the body that experience the time correction force in the space dimension) as a result of the collision along the time dimension with "event mass" that stopped due to the destruction of its time singularity that drove it forward originally.
We collide with "event mass" along our time line (our straight path in the time dimension). If we are not associated with the invention (that disappeared in time), then such "event mass" does not exist along our time line, in this way this time correction has a strange property that only bodies associated with the invention experience the force directly, irrespective of their location in space.
This is good, for a start to quantify such a strange force in space as a result of effects in time. Can we time travel using such a force?
Have a nice day.
Note: The biggest time singularity is the Big Bang or Creation itself.
Tuesday, November 17, 2015
Hard elytra And Scaly Wings
If insects rely on a negative temperature particle spinning around positive energy particles producing an anti-gravity effect for flight, then either the insects carries positive temperature particles or negative temperature particles. In the former case, the insect will seek low temperature ambiance places to fly in, and the latter high temperature ambiance place for flight. So, we have a hot wing and a cold wing. It is likely that a hot wing is hard in order to remain hot longer, and a cold wing is light and scaly to remain cool.
And so, hard winged insects (carrying positive temperature particle) seek low temperature environment and light scaly winged insects (carrying negative temperature particles) seek high temperature environment.
An electric field (electric static) applied to the elytra of a pood beetle, Dytiscidae, aligns/orientates the molecular structures holding the coupled pair of temperature particles and so directs the gravitational field in a specific direction.
The anti-gravitational effects of an elytra will disappear as ambient temperature raises.
Then, there are scaly butterfly wings.
Both types of wings are made of chitin; it is the micro structures on the wings that determine which type of temperature particles are in hold for controlled flight.
Speculatively yours.
And so, hard winged insects (carrying positive temperature particle) seek low temperature environment and light scaly winged insects (carrying negative temperature particles) seek high temperature environment.
An electric field (electric static) applied to the elytra of a pood beetle, Dytiscidae, aligns/orientates the molecular structures holding the coupled pair of temperature particles and so directs the gravitational field in a specific direction.
The anti-gravitational effects of an elytra will disappear as ambient temperature raises.
Then, there are scaly butterfly wings.
Both types of wings are made of chitin; it is the micro structures on the wings that determine which type of temperature particles are in hold for controlled flight.
Speculatively yours.
Saturday, October 31, 2015
Anti-Blackholes And A Party Of Six, Cosmic
If a blackhole is a mass of negative gravity particles so dense that the potential field around it holds back particles at light speed, then equivalently there can be two new types of blackhole one due to a collection of negative charge particles, and another due to negative temperature particles. Remember that from post "Particle Clouds" dated 13 Jul 2015, a particle can reside in the \(\psi\) of another particle of the same type; as the graphs of \(F_v\), force density around any particle, show, particles of the same type are attracted to each other in close proximity (eg. post "Less Mass But No Theoretical Mass" dated 23 Nov 2014).
In an analogous way, a group of positive particles so dense, can set up a potential field around them that even particles with light speed cannot approach. As kinetic energy is traded for potential energy, the approaching particles are reduced to zero speed before reaching the group of positive particles; forming a ring of lights around the group of particles. A sort of anti-blackholes due to positive gravity particles, positive charge particles and positive temperature particles. However, since positive particles does not attract each other at close proximity without at least one of them being heavier in mass (possibly made artificially more massive), anti-blackhole may not be as common.
In total, six particle phenomenons, three types of blackhole and three types of anit-blackhole, all with mega effects visible at the cosmic level.
Cosmic Insanity!
In an analogous way, a group of positive particles so dense, can set up a potential field around them that even particles with light speed cannot approach. As kinetic energy is traded for potential energy, the approaching particles are reduced to zero speed before reaching the group of positive particles; forming a ring of lights around the group of particles. A sort of anti-blackholes due to positive gravity particles, positive charge particles and positive temperature particles. However, since positive particles does not attract each other at close proximity without at least one of them being heavier in mass (possibly made artificially more massive), anti-blackhole may not be as common.
In total, six particle phenomenons, three types of blackhole and three types of anit-blackhole, all with mega effects visible at the cosmic level.
Cosmic Insanity!
Friday, October 30, 2015
It's Nu-clue-lar
If the heat released in a big explosion is due to positive temperature particles, then there is also a negative temperature particles front, which have less mass, before the high temperature heat front.
Ever witness a nuclear test? There is also a EMP (electro-magnetic pusle) due to a electron front, and a blast wave due to protons.
Spinning electrons generates magnetic fields and spinning protons generate gravitational fields. The generated gravitational fields lift objects into the air; the anti-gravitational effects in a blast wave is not due to strong winds (air current).
Then, there are the positive and negative gravitational particles. Both would be secondary wave fronts; a secondary EMP but now positive, and a secondary heat front.
In all cases, force fields due to the particles and due to their spins are manifested, so there are six paired wave fronts, electro(n)-magnetic, proton-gravity, negative temperature-gravity, positive temperature-electric, negative gravity-magnetic and positive gravity-electric.
KaBloom!
Ever witness a nuclear test? There is also a EMP (electro-magnetic pusle) due to a electron front, and a blast wave due to protons.
Spinning electrons generates magnetic fields and spinning protons generate gravitational fields. The generated gravitational fields lift objects into the air; the anti-gravitational effects in a blast wave is not due to strong winds (air current).
Then, there are the positive and negative gravitational particles. Both would be secondary wave fronts; a secondary EMP but now positive, and a secondary heat front.
In all cases, force fields due to the particles and due to their spins are manifested, so there are six paired wave fronts, electro(n)-magnetic, proton-gravity, negative temperature-gravity, positive temperature-electric, negative gravity-magnetic and positive gravity-electric.
KaBloom!
Thursday, October 29, 2015
Where Is The Flying Shopping Cart?
Which leads us back to,
The cold body provides the negative temperature particles and the hot body provides the positive temperature particles, but where is the composite of a negative particle in rotation around a positive particle(s) nucleus that creates a gravitational field?
In the hot body? In the cold body? In the supportive structure?
Answer: Mostly on the hot body.
The cold body provides the negative temperature particles and the hot body provides the positive temperature particles, but where is the composite of a negative particle in rotation around a positive particle(s) nucleus that creates a gravitational field?
In the hot body? In the cold body? In the supportive structure?
Answer: Mostly on the hot body.
Sunday, October 25, 2015
Making Waves
These people need a reminder of what I can do! Maths and more maths.
After acquiring a negative temperature particle in orbit around/in a positive temperature particle (or a group of positive temperature particles), the fluid particle develops a gravitational field along the axis of rotation. This force when directed against earth's gravity, lifts the fluid particle. When the fluid particle is also in rotation, the combined effect is the characteristic profile of a wave.
The maximum ascending gradient of the wave profile occurs at,
\(g_{max,\,asc}=g_w-g_e\)
when the fluid particle acquired gravitational force opposes earth's gravity directly.
The maximum point of the wave profile occurs when,
\(g_e-g_w=0\)
when the fluid particle acquired gravitational force cancels earth's gravity and continues to rotates into the direction of earth's gravity, downwards. When the fluid particle acquired gravitational force adds to earth's gravity, the fluid particle descends with greater acceleration than its ascendance.
\(g_{max,\,des}=g_w+g_e\)
As,
\(g_w+g_e\gt g_w-g_e\)
\(g_{max,\,des}\gt g_{max,\,asc}\)
This gives the characteristic short downward curve of the wave.
After acquiring a negative temperature particle in orbit around/in a positive temperature particle (or a group of positive temperature particles), the fluid particle develops a gravitational field along the axis of rotation. This force when directed against earth's gravity, lifts the fluid particle. When the fluid particle is also in rotation, the combined effect is the characteristic profile of a wave.
The maximum ascending gradient of the wave profile occurs at,
\(g_{max,\,asc}=g_w-g_e\)
when the fluid particle acquired gravitational force opposes earth's gravity directly.
The maximum point of the wave profile occurs when,
\(g_e-g_w=0\)
when the fluid particle acquired gravitational force cancels earth's gravity and continues to rotates into the direction of earth's gravity, downwards. When the fluid particle acquired gravitational force adds to earth's gravity, the fluid particle descends with greater acceleration than its ascendance.
\(g_{max,\,des}=g_w+g_e\)
As,
\(g_w+g_e\gt g_w-g_e\)
\(g_{max,\,des}\gt g_{max,\,asc}\)
This gives the characteristic short downward curve of the wave.
Wednesday, October 21, 2015
Hot Air!
Hot air balloons,
A mix of cold and hot air on the left balloon creates lift, the balloon on the right where air is heated inside however, does not have lift. The balloon on the right is inflated but does not generate lift.
Still hot air.
Note: Yes, a floating body displaces its own weight and a submerged body experiences lift due to the pressure difference on the top and bottom effective areas. The question here is: why hot air has lift and rises? More importantly, how hot air acquire lift and rises? The shape of the inflated balloon is the result of hot air rising, not the cause of hot air rising and not the ultimate cause of the balloon rising.
A mix of cold and hot air on the left balloon creates lift, the balloon on the right where air is heated inside however, does not have lift. The balloon on the right is inflated but does not generate lift.
Still hot air.
Note: Yes, a floating body displaces its own weight and a submerged body experiences lift due to the pressure difference on the top and bottom effective areas. The question here is: why hot air has lift and rises? More importantly, how hot air acquire lift and rises? The shape of the inflated balloon is the result of hot air rising, not the cause of hot air rising and not the ultimate cause of the balloon rising.
Friday, October 16, 2015
Wind, Eddies, Vortices And Turbulence
This will model as a gas molecule,
a negative temperature particle in orbit around a positive temperature particle. This model will drop at higher than earth's gravity when pointing downwards, roll about, and be weightless when pointing upwards.
a negative temperature particle in orbit around a positive temperature particle. This model will drop at higher than earth's gravity when pointing downwards, roll about, and be weightless when pointing upwards.
Thursday, October 15, 2015
Hot Water Dripped Onto Cold Water
Hot water dripped onto cold water will vaporize immediately as positive temperature particles acquire negative temperature particle. The negative particle in orbit around the positive temperature particles, generates a gravitational field along its axis of rotation and acts against gravity. Hot water becomes a gas.
The same happens when hot water is poured out into the open at ambient \(-40^oC\), the steam observed is not water freezing immediately, but having acquired negative temperature particles, the hot water is weightless and drifts away like a mist.
Both experiments were posted on youtube.
Have a nice day.
The same happens when hot water is poured out into the open at ambient \(-40^oC\), the steam observed is not water freezing immediately, but having acquired negative temperature particles, the hot water is weightless and drifts away like a mist.
Both experiments were posted on youtube.
Have a nice day.
Gas Lots of Gas
In the gaseous state, it might seems that it is the spinning negative temperature particles which present a positive gravitational force directed along their axes of rotation that counter earth's gravity and enables the material to break free and fly off.
In this case, we would have assigned the signs of temperature particles wrong.
It is the positive temperature particles that attract a negative temperature particle to spin around them and so manifest a gravitational force that counteracts gravity. This turns the material into a gas. Since, temperature particles are discrete entity, it is possible that the material breaks away without passing through the liquid state on the acquisition of an negative temperature particle, Sublime.
A negative temperature particle spinning by itself, may generate enough gravitational force along its axis of spin to counter gravity. When this happens, at low temperature, the material also attains a gaseous state. The material evaporates away on the exposed surface. A sort of cold corrosion.
A fluid boiling, occurs at the fluid/container contact surface, and evaporation occurs on the surface of the fluid. Both occur where it is possible for positive temperature particles to attract negative temperature particles.
All these introduce a new factor in the transition to the gaseous state, the need to acquire negative temperature particles. These particles in orbit around positive temperature particles generates a positive gravitational field that counters earth's gravity.
Volar! jYo puedo volar!
In this case, we would have assigned the signs of temperature particles wrong.
It is the positive temperature particles that attract a negative temperature particle to spin around them and so manifest a gravitational force that counteracts gravity. This turns the material into a gas. Since, temperature particles are discrete entity, it is possible that the material breaks away without passing through the liquid state on the acquisition of an negative temperature particle, Sublime.
A negative temperature particle spinning by itself, may generate enough gravitational force along its axis of spin to counter gravity. When this happens, at low temperature, the material also attains a gaseous state. The material evaporates away on the exposed surface. A sort of cold corrosion.
A fluid boiling, occurs at the fluid/container contact surface, and evaporation occurs on the surface of the fluid. Both occur where it is possible for positive temperature particles to attract negative temperature particles.
All these introduce a new factor in the transition to the gaseous state, the need to acquire negative temperature particles. These particles in orbit around positive temperature particles generates a positive gravitational field that counters earth's gravity.
Volar! jYo puedo volar!
Wednesday, October 14, 2015
Why Melt? A Solid Is Magnetic
Oxygen \(O\), that exists as a gas, \(O_2\), at room temperature suggests the absence of negative gravity particles in spin that manifest a magnetic force that holds the material as a solid. Temperature particles (positive and negative particles) in spin present the electrostatic force or the gravitational force. Both these forces are weak and do not hold a material solid. And, as we extend the model to include many negative gravity particles, a resultant magnetic force is the result of an unbalanced spin among the spinning particles.
Statements more suitable in a religious context than science.
But none the less, this proposed effect of unbalance spinning negative gravity particle, is consistent with the fact that carbon \(C\) (less atomic mass but with unbalanced spinning negative gravity particles), is a solid but nitrogen \(N\) (more atomic mass but without unbalanced spinning negative gravity particles), is a gas, \(N_2\) at room temperature.
This conjuncture still allows for increasing atomic mass with increasing number of negative gravity particles across the Periodic Table, as we expect intuitively. So, it is wrong to say \(O\), has no gravity particles. It has mass! Instead, \(O_2\) has no unbalanced spinning negative gravity particles.
And it is the spins of negative gravity particles that matters. In the case of large cosmic spin, the presence of this magnetic field along the axis of rotation of negative gravity particles, collapses all magnetic material into a disc perpendicular to the axis of rotation.
Yes, I am building my very own, personal universe.
The introduction of positive temperature particles (heat) weakens a solid and at high enough temperature melts the solid, ie the melting point. The introduction of negative temperature particles (freeze) also weakens a solid and at low enough temperature causes it to fracture. We should call this temperature the fracturing point. The difference is: Positive temperature particles in spins manifest a electrostatic force that interacts with positive charges in the material and repels the material apart; at its melting point the material flows apart. Negative temperature particles on the other hand manifests a gravitation force in spins, this force however attracts the negative gravity particles in the material. The material hold firm at low temperature, but fractures. The force that holds a solid rigid is the magnetic force, "carried by" temperature particles and is weakened by the introduction of temperature particles into the material.
What of positive gravity particles?? Particles with gravity field lines pointing outwards??
mass \(\equiv\) negative gravity particles
positive gravity particles \(\equiv\) ??
Statements more suitable in a religious context than science.
But none the less, this proposed effect of unbalance spinning negative gravity particle, is consistent with the fact that carbon \(C\) (less atomic mass but with unbalanced spinning negative gravity particles), is a solid but nitrogen \(N\) (more atomic mass but without unbalanced spinning negative gravity particles), is a gas, \(N_2\) at room temperature.
This conjuncture still allows for increasing atomic mass with increasing number of negative gravity particles across the Periodic Table, as we expect intuitively. So, it is wrong to say \(O\), has no gravity particles. It has mass! Instead, \(O_2\) has no unbalanced spinning negative gravity particles.
And it is the spins of negative gravity particles that matters. In the case of large cosmic spin, the presence of this magnetic field along the axis of rotation of negative gravity particles, collapses all magnetic material into a disc perpendicular to the axis of rotation.
Yes, I am building my very own, personal universe.
The introduction of positive temperature particles (heat) weakens a solid and at high enough temperature melts the solid, ie the melting point. The introduction of negative temperature particles (freeze) also weakens a solid and at low enough temperature causes it to fracture. We should call this temperature the fracturing point. The difference is: Positive temperature particles in spins manifest a electrostatic force that interacts with positive charges in the material and repels the material apart; at its melting point the material flows apart. Negative temperature particles on the other hand manifests a gravitation force in spins, this force however attracts the negative gravity particles in the material. The material hold firm at low temperature, but fractures. The force that holds a solid rigid is the magnetic force, "carried by" temperature particles and is weakened by the introduction of temperature particles into the material.
What of positive gravity particles?? Particles with gravity field lines pointing outwards??
mass \(\equiv\) negative gravity particles
positive gravity particles \(\equiv\) ??
Monday, October 12, 2015
No Inner Electron Shells.
The manifestation of physical phases (solid, liquid, gas) of a material involved all interactions of the six basic particles (electron, protons, positive temperature, negative temperature,positive gravity and negative gravity .
The direct interactions of the particles are strong forces. The interaction of a particle and another in spin is a weaker force. The particle in spin or rotational motion manifest the orthogonal oscillating dimension. This force is along the axis of rotation and is highly directional. This force is reversed when the sense of the rotation reverses.
The interactions of spinning/rotating particles are the weakest force. This force reverses as the particles changes directions, is transient and may only be observable averaged over time and aggregated over many particles.
Water presents itself as magnetic because of the relative prominence of temperature particles. The molecular structure of water points that oxygen \(O\), is the key factor. This also suggests that, maybe, elements down a column in the periodic table with the same outer electron configuration have increasing numbers of temperature particles; that inner shell electrons do not exist!
As suggested previously in the post "Magnetism And Temperature Particles" dated 11 Jul 2015, to the relationship of magnetism and temperature particles, we add: an abundance of positive temperature particles made the element diamagnetic and an abundance of negative temperature particles made the element ferromagnetic. In between is paramagnetism due to the aligned rotations of the charged particles in the material. (When ferromagnetism and paramagnetism add negatively, we have anti-ferromagnetism)
Have a nice day.
The direct interactions of the particles are strong forces. The interaction of a particle and another in spin is a weaker force. The particle in spin or rotational motion manifest the orthogonal oscillating dimension. This force is along the axis of rotation and is highly directional. This force is reversed when the sense of the rotation reverses.
The interactions of spinning/rotating particles are the weakest force. This force reverses as the particles changes directions, is transient and may only be observable averaged over time and aggregated over many particles.
Water presents itself as magnetic because of the relative prominence of temperature particles. The molecular structure of water points that oxygen \(O\), is the key factor. This also suggests that, maybe, elements down a column in the periodic table with the same outer electron configuration have increasing numbers of temperature particles; that inner shell electrons do not exist!
As suggested previously in the post "Magnetism And Temperature Particles" dated 11 Jul 2015, to the relationship of magnetism and temperature particles, we add: an abundance of positive temperature particles made the element diamagnetic and an abundance of negative temperature particles made the element ferromagnetic. In between is paramagnetism due to the aligned rotations of the charged particles in the material. (When ferromagnetism and paramagnetism add negatively, we have anti-ferromagnetism)
Have a nice day.
Wednesday, August 26, 2015
Magnetic Water But First Adjusting Lambert
If water is magnetic, how does it work? Water being magnetic will help explain the formation of water droplets, but that would be jumping the gun.
What else is in optics? Plenty!
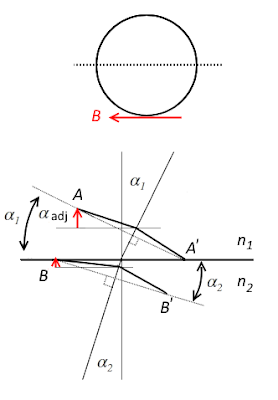
In the case of Lambert's cosine law, where intensity is directly proportional to the incident angle, but as noted in the post "No \(B\), Speed Alone" dated 25 Aug 2015, since the two loops makes an angle \(\theta\) with the ray,
\(cos(\alpha)\to cos(\alpha_{adj})=cos(\alpha+90^o-\theta)=-sin(\alpha-\theta)=sin(\theta-\alpha)\)
and
\(cos(\alpha)\to cos(\alpha_{adj})=cos(\alpha-90^o+\theta)=sin(\alpha+\theta)\)
as we adjust for the angle of incident between the loops and the surface normal at the point of reflection, we have an adjusted Lambert, where the intensity of an ideal diffusely reflecting surface is proportional to,
\(sin(\theta-\alpha)+sin(\theta+\alpha)=sin(\theta)cos(\alpha)\)
\(\alpha\) is the incident angle of the ray, and \(\theta\) is the angle the loops make with the ray, polarization.
Since \(\theta\) is distributed over a range of values, \(0\lt\theta\lt\pi/2\), intensity \(I\),
\(I\propto\int^{\pi/2}_0{f(\theta)sin(\theta)}d\theta.cos(\alpha)\)
where
\(f(\theta)=\cfrac{2\theta}{\pi(1+\theta^4)}\)
from the post "Not Exactly A Fluorescence Polarizer" dated 28 Jul 2015. The problem is with the abrupt cutoff at \(\pi/2\), may be
\(I\propto\int^{\theta\to\infty}_0{f(\theta)sin(\theta)}d\theta.cos(\alpha)\)
or even,
\(I\propto\int^{\theta\to\infty}_{\theta\to -\infty}{f(\theta)sin(\theta)}d\theta.cos(\alpha)\)
Only after \(\theta\) has been accounted for, (for example, \(\theta=90^o\)) is it possible to have a constant \(A\) such that,
\(I=AF(\theta).cos(\alpha)\)
where \(F(\theta)\) is a function of \(\theta\) only. In the case \(\theta=90^o\), a laser source,
\(I=A.cos(\alpha)\)
where \(A\) is a constant.
What else is in optics? Plenty!
In the case of Lambert's cosine law, where intensity is directly proportional to the incident angle, but as noted in the post "No \(B\), Speed Alone" dated 25 Aug 2015, since the two loops makes an angle \(\theta\) with the ray,
\(cos(\alpha)\to cos(\alpha_{adj})=cos(\alpha+90^o-\theta)=-sin(\alpha-\theta)=sin(\theta-\alpha)\)
and
\(cos(\alpha)\to cos(\alpha_{adj})=cos(\alpha-90^o+\theta)=sin(\alpha+\theta)\)
as we adjust for the angle of incident between the loops and the surface normal at the point of reflection, we have an adjusted Lambert, where the intensity of an ideal diffusely reflecting surface is proportional to,
\(sin(\theta-\alpha)+sin(\theta+\alpha)=sin(\theta)cos(\alpha)\)
\(\alpha\) is the incident angle of the ray, and \(\theta\) is the angle the loops make with the ray, polarization.
Since \(\theta\) is distributed over a range of values, \(0\lt\theta\lt\pi/2\), intensity \(I\),
\(I\propto\int^{\pi/2}_0{f(\theta)sin(\theta)}d\theta.cos(\alpha)\)
where
\(f(\theta)=\cfrac{2\theta}{\pi(1+\theta^4)}\)
from the post "Not Exactly A Fluorescence Polarizer" dated 28 Jul 2015. The problem is with the abrupt cutoff at \(\pi/2\), may be
\(I\propto\int^{\theta\to\infty}_0{f(\theta)sin(\theta)}d\theta.cos(\alpha)\)
or even,
\(I\propto\int^{\theta\to\infty}_{\theta\to -\infty}{f(\theta)sin(\theta)}d\theta.cos(\alpha)\)
Only after \(\theta\) has been accounted for, (for example, \(\theta=90^o\)) is it possible to have a constant \(A\) such that,
\(I=AF(\theta).cos(\alpha)\)
where \(F(\theta)\) is a function of \(\theta\) only. In the case \(\theta=90^o\), a laser source,
\(I=A.cos(\alpha)\)
where \(A\) is a constant.
Tuesday, August 25, 2015
No \(B\), Speed Alone
Why does total internal reflection occur?
From the post "Wave Front and Wave Back" dated 18 May 2014, a photon was conceptualized as a particle in helical motion,
\(\cfrac{x_{v1}}{cos(\alpha_1)}=\cfrac{x_{v2}}{cos(\alpha_2)}\)
\(x_{v2}=x_{v1}\cfrac{cos(\alpha_2)}{cos(\alpha_1)}\)
where \(x_{v1}\), \(x_{v2}\) are the radii of circular motion in medium 1 and 2 respectively.
and
\(\cfrac{\lambda}{n_1sin(\alpha_1)}=\cfrac{\lambda}{n_2sin(\alpha_2)}\)
\(sin(\alpha_2)=\cfrac{n_1}{n_2}sin(\alpha_1)\)
So,
\(x_{v2}=\cfrac{x_{v1}}{cos(\alpha_1)}\sqrt{1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)}\)
when the particle enters into to less dense medium,
\(n_2\lt n_1\)
\(1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)\lt 0\)
in which case, \(x_{v2}\) is complex and is rotated by \(90^o\) clockwise at the point of ncident,
\(x_{v2}=i.\cfrac{x_{v1}}{cos(\alpha_1)}\sqrt{\left|1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)\right|}\)
and \(\alpha_2\) is totally internally reflected. When
\(1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)=0\)
\(sin(\alpha_1)=sin(\alpha_c)=\cfrac{n_2}{n_1}\)
where \(\alpha_c\) is the critical angle. Unfortunately, the formula is valid only up to \(\alpha_c\). For incident angle greater than \(\alpha_c\), we know that the ray is reflected,
\(x_{v2}={x_{v1}}\)
\(1=\cfrac{cos(\alpha_2)}{cos(\alpha_1)}\)
\(\alpha_1=\alpha_2\)
both angles measured from the normal on medium \(n_1\).
This derivation for total internal reflection considers the relative speeds of the particle in the two mediums alone; \(B\) fields are not involved. Since, both loops are perpendicular to the ray \(\alpha\) only in the limiting case of \(\theta\to90^o\), the following adjustments are necessary to the values of \(\alpha\) for each of the loop as illustrated,
\(\alpha_{adj}=\alpha+90^o-\theta\)
and
\(\alpha_{adj}=\alpha-90^o+\theta\)
which indicate that the two loops can be separated (circular polarization\(\to\)linear polarization) when,
since \(\alpha\lt90^o\)
\(\alpha-90^o+\theta\lt\alpha_c\)
\(\alpha\lt\alpha_c+90^o-\theta\)
and
\(\alpha+90^o-\theta\gt\alpha_c\)
\(\alpha\gt\alpha_c-90^o+\theta\)
where \(\alpha_{2}^{'}\) has been totally internally reflected. When \(\theta\to90^o\), the range of \(\alpha\) collapses to a single value \(\alpha_c\), as \(\alpha_{adj}\to\alpha\).
From the post "Wave Front and Wave Back" dated 18 May 2014, a photon was conceptualized as a particle in helical motion,
\(\cfrac{x_{v1}}{cos(\alpha_1)}=\cfrac{x_{v2}}{cos(\alpha_2)}\)
\(x_{v2}=x_{v1}\cfrac{cos(\alpha_2)}{cos(\alpha_1)}\)
where \(x_{v1}\), \(x_{v2}\) are the radii of circular motion in medium 1 and 2 respectively.
and
\(\cfrac{\lambda}{n_1sin(\alpha_1)}=\cfrac{\lambda}{n_2sin(\alpha_2)}\)
\(sin(\alpha_2)=\cfrac{n_1}{n_2}sin(\alpha_1)\)
So,
\(x_{v2}=\cfrac{x_{v1}}{cos(\alpha_1)}\sqrt{1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)}\)
when the particle enters into to less dense medium,
\(n_2\lt n_1\)
\(1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)\lt 0\)
in which case, \(x_{v2}\) is complex and is rotated by \(90^o\) clockwise at the point of ncident,
\(x_{v2}=i.\cfrac{x_{v1}}{cos(\alpha_1)}\sqrt{\left|1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)\right|}\)
and \(\alpha_2\) is totally internally reflected. When
\(1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)=0\)
\(sin(\alpha_1)=sin(\alpha_c)=\cfrac{n_2}{n_1}\)
where \(\alpha_c\) is the critical angle. Unfortunately, the formula is valid only up to \(\alpha_c\). For incident angle greater than \(\alpha_c\), we know that the ray is reflected,
\(x_{v2}={x_{v1}}\)
\(1=\cfrac{cos(\alpha_2)}{cos(\alpha_1)}\)
\(\alpha_1=\alpha_2\)
both angles measured from the normal on medium \(n_1\).
This derivation for total internal reflection considers the relative speeds of the particle in the two mediums alone; \(B\) fields are not involved. Since, both loops are perpendicular to the ray \(\alpha\) only in the limiting case of \(\theta\to90^o\), the following adjustments are necessary to the values of \(\alpha\) for each of the loop as illustrated,
\(\alpha_{adj}=\alpha+90^o-\theta\)
and
\(\alpha_{adj}=\alpha-90^o+\theta\)
which indicate that the two loops can be separated (circular polarization\(\to\)linear polarization) when,
since \(\alpha\lt90^o\)
\(\alpha-90^o+\theta\lt\alpha_c\)
\(\alpha\lt\alpha_c+90^o-\theta\)
and
\(\alpha+90^o-\theta\gt\alpha_c\)
\(\alpha\gt\alpha_c-90^o+\theta\)
where \(\alpha_{2}^{'}\) has been totally internally reflected. When \(\theta\to90^o\), the range of \(\alpha\) collapses to a single value \(\alpha_c\), as \(\alpha_{adj}\to\alpha\).
Fractured Science
What happens when \(\theta=90^o-\alpha\)?
In this case, the loop parallel to the interface passes through the medium unrefracted (there is no refraction due to the boundary conditions on \(B\), but the ray is still refracted due to a change in velocity of the ray). The other loop is reflected and the center line of this ray intersects the interface behind the point of reflection and
\(d\lt0\)
\(d\), the lateral shift is negative.
When \(\theta=\alpha\),
One loop passes perpendicularly into the less dense medium at the point of reflection and is refracted in the less dense medium as the result of an increase in velocity. The other is reflected when the incident angle \(\alpha\gt\) critical angle.
Notice that as the right loop enters into the less dense medium, the particle has a parallel velocity component that is opposite to the parallel velocity component of the ray. The particle is travelling in the reverse direction to the ray, along the interface. And the adjusted angle that the loop makes with the normal is,
\(\alpha_{adj}=-\left( 90^{ o }-\alpha -\theta \right) \)
this suggest that the ray is refracted back into the same side of the normal as the incident ray,
which would be very odd indeed.
This approach is flawed as the underlying mechanism of total internal reflection possibly as the result of applying boundary conditions on the ray's \(B\) field has not been explored yet. Previously, there is a change in direction in the ray, as its normal and parallel \(B\) field components are effected differently at the boundary.
Note: If, however changes in speed alone can provide for total internal reflection (post "No \(B\), Speed Alone" dated 25 Aug 2015), then the above can be superimposed onto the results for total internal reflection as before.
In this case, the loop parallel to the interface passes through the medium unrefracted (there is no refraction due to the boundary conditions on \(B\), but the ray is still refracted due to a change in velocity of the ray). The other loop is reflected and the center line of this ray intersects the interface behind the point of reflection and
\(d\lt0\)
\(d\), the lateral shift is negative.
When \(\theta=\alpha\),
One loop passes perpendicularly into the less dense medium at the point of reflection and is refracted in the less dense medium as the result of an increase in velocity. The other is reflected when the incident angle \(\alpha\gt\) critical angle.
Notice that as the right loop enters into the less dense medium, the particle has a parallel velocity component that is opposite to the parallel velocity component of the ray. The particle is travelling in the reverse direction to the ray, along the interface. And the adjusted angle that the loop makes with the normal is,
\(\alpha_{adj}=-\left( 90^{ o }-\alpha -\theta \right) \)
this suggest that the ray is refracted back into the same side of the normal as the incident ray,
which would be very odd indeed.
This approach is flawed as the underlying mechanism of total internal reflection possibly as the result of applying boundary conditions on the ray's \(B\) field has not been explored yet. Previously, there is a change in direction in the ray, as its normal and parallel \(B\) field components are effected differently at the boundary.
Note: If, however changes in speed alone can provide for total internal reflection (post "No \(B\), Speed Alone" dated 25 Aug 2015), then the above can be superimposed onto the results for total internal reflection as before.
Yet Another Time Singularity
Goos–Hänchen effect? Where \(n_2\lt n_1\),
The particle on the lower loop and the upper loop, where the last point to enter into the second medium is the earliest and the latest respectively, are reflected at different points along the interface. The ray splits into two beams. In order to be reflected, this last point is lifted off the interface just as it enters into the second medium. The distance between the two point of reflection,
\(d=2x_vsin(\theta).\cfrac{1}{sin(90^o-\alpha)}\)
where \(x_v\) is the radius of circular motion of the particle displace from the \(\psi\) cloud center. The separation between the two rays is,
\(d_b=d.{sin(90^o-\alpha)}=2x_vsin(\theta)\)
where \(x_v\) is the radius of circular motion of the particle displace from the \(\psi\) cloud center. The separation between the two rays is,
\(d_b=d.{sin(90^o-\alpha)}=2x_vsin(\theta)\)
Since the particle are reflected off at different times, there is also a phase shift between the lower and upper loop. The \(E\) fields due to the rotating particles on the two loops are both in the same direction. These are linearly polarized light.
When \(\theta\lt90^o-\alpha\),
Both loops leave the second medium at the apex of the cone. There is no phase shift between the two loops. Both loops are reflected off at the point of reflection. The \(E\) fields due to the rotating particles on the two loops radiate from a common center; the ray remains circularly polarized.
Both instances suggest that the cause of such shifts are inherent in the nature of emitted fluorescence and not of the reflecting interface.
Sunday, August 23, 2015
Shield And All Flavors Of Photons.
When \(\small{\beta\to90^o}\), \(\small{\theta\to0^o}\), we see as the aura around a torch on the side of the light source,
If we pulse this emission (\(\small{\beta\to90^o}\)) at an appropriate energy density, \(\psi\) natural frequency, we have a shield that in the absence of a similar energy density field is attractive and in the presence of a similar energy density field repulsive.
This torch emits photons appropriate for the force needed. For example, photons carrying gravitational energy,
The frequency of \(\psi\) around these particles will be high given their size, but the source of this photons can be pulsed to produce an appropriate force field frequency.
But how to create a photon source that is the opposite of a laser; \(\small{\beta\to90^o}\) as oppose to \(\small{\beta\to0^o}\)?
If we pulse this emission (\(\small{\beta\to90^o}\)) at an appropriate energy density, \(\psi\) natural frequency, we have a shield that in the absence of a similar energy density field is attractive and in the presence of a similar energy density field repulsive.
This torch emits photons appropriate for the force needed. For example, photons carrying gravitational energy,
The frequency of \(\psi\) around these particles will be high given their size, but the source of this photons can be pulsed to produce an appropriate force field frequency.
But how to create a photon source that is the opposite of a laser; \(\small{\beta\to90^o}\) as oppose to \(\small{\beta\to0^o}\)?
Saturday, August 22, 2015
Binomial Dispersion
Absorption and emission along the ray, as Huygens' point source can account for dispersion that is binomial,
where the probability of making a turn of \(\beta=90^o-\theta\) is half. The intensity of the ray decreases by \(\small{\left(\cfrac{1}{2}\right)^n}\), \(n\) point source away from the direction of the original ray.
\(\theta\) is polarization.
In the case of a laser, when the \(E\) fields are parallel to the direction of the ray, and \(\small{\theta\to90^o}\), there is no dispersion because \(\small{\beta=0}\).
When the \(E\) fields are perpendicular to the direction of the ray \(\small{\theta\to0}\), light has stop propagating forward and has spread in the direction perpendicular to the initial direction of travel. In this case, \(\small{\beta=90^o}\).
The problem with this view is that the ray attenuates too quickly along the direction of the ray, from point source to point source. Given any light source, there has to be a spread of \(\small{\theta}\) vales such that light that project forward to considerable distance has \(\small{\theta\approx90^o}\), \(\small{\beta\approx0}\).
where the probability of making a turn of \(\beta=90^o-\theta\) is half. The intensity of the ray decreases by \(\small{\left(\cfrac{1}{2}\right)^n}\), \(n\) point source away from the direction of the original ray.
\(\theta\) is polarization.
In the case of a laser, when the \(E\) fields are parallel to the direction of the ray, and \(\small{\theta\to90^o}\), there is no dispersion because \(\small{\beta=0}\).
When the \(E\) fields are perpendicular to the direction of the ray \(\small{\theta\to0}\), light has stop propagating forward and has spread in the direction perpendicular to the initial direction of travel. In this case, \(\small{\beta=90^o}\).
The problem with this view is that the ray attenuates too quickly along the direction of the ray, from point source to point source. Given any light source, there has to be a spread of \(\small{\theta}\) vales such that light that project forward to considerable distance has \(\small{\theta\approx90^o}\), \(\small{\beta\approx0}\).
Friday, August 21, 2015
Huygens' Principle Re-emitted
Repeated absorption and emission of photons provides a physical basis for Huygens' principle, where every point in the path of the light ray is considered a new point source. This "new point source" is the particle that absorbs photons and emits them, along the light ray (wave front).
However, the emission in this case is in the direction perpendicular to the direction of travel of the particle, in either \(\beta=90^o-\theta\) or \(-\beta\), not in all directions perpendicular to a circular wave front.
However, the emission in this case is in the direction perpendicular to the direction of travel of the particle, in either \(\beta=90^o-\theta\) or \(-\beta\), not in all directions perpendicular to a circular wave front.
Pumping position down! Lightly, lightly, lightly!
Then Reflected
From the post "Photon Emission After Absorption" dated 25 Jul 2015, the photon is ejected perpendicular to the direction of travel of the particle; in the post "A Pump!" dated 25 Jul 2015,
\(E_{p}=h.\left\{1-\sqrt{\cfrac{sin(\theta)}{cos(\theta)}}\right\}.f_{cir}\)
when
\(1-\sqrt{\cfrac{sin(\theta)}{cos(\theta)}}\lt0\)
\(\sqrt{\cfrac{sin(\theta)}{cos(\theta)}}\gt1\)
a photon is absorbed first then emitted, this introduces a \(\small{\pi}\) phase in the emission.
The refracted ray we observe in the second medium is made up of emitted photons in the direction perpendicular to \(\alpha_2\) (out of the paper). This emitted ray will be absorbed and be emitted a second time. In the first instance of emission, the photons are emitted perpendicular to the direction of travel of the particle (\(P^{'}O\) and \(PO\)), and is along \(E\,\,PE^{'}\) and \(E\,\,PE\). The direction of incident then changes to from \(PO\) to \(EO\), by a difference of \(90^o-\theta\). Along \(EO\) particles interact with the passing photons, as if along \(PO\).
The ray \(\alpha_2\) corresponds to the line \(EO\). \(EO\) is absorbed and emitted into the direction it was first absorbed. It is diverted by a difference of \(-(90^o-\theta)\) to be along \(PO\) again. Reciprocity.
If we confine photon emission/absorption to be at the point of incident, this emitted ray, \(PO\) will result in a reflected ray,
And the possibility of a phase lag between the absorption of a photon first, then an emission, accounts for the possible \(\pi\) phase shift in the reflected ray.
This is not the reflected ray off a mirrored surface, but reflection from an interface of two mediums with different optical properties. The reflected ray is the result of a second absorption/emission of the photons in the medium, the first absorption/emission allows us to see \(\alpha_2\). The second absorption/emission is due to the interaction of \(\alpha_2\) with the medium. \(\alpha_2\) interacts with the medium only once. The first absorption/emission of the photons in the medium results in the cone \(PE^{'}\,\,E\,\,PE\) from which we started to derive the geometry of \(\alpha_2\) (post "It's All Fluorescence Outside, Inside" dated 29 Jul 2015).
The ray corresponding to \(90^o-\theta_2-\alpha_2\) is probably totally internally reflected. The presence of this ray is important to vindicate the results here. It is possible that not all of this ray is absorbed and emitted to result in a reflected ray.
When would absorption and emission stop? Absorb along \(AB\) \(\to\) emit perpendicularly \(XY\) \(\to\) absorb along \(XY\) \(\to\) emit perpendicularly along \(AB\), return. The photons are emitted in the direction perpendicular to the particle's travel; this is not in the direction perpendicular to the ray on the plane containing the axis of the cone. This emitted ray is rotated about the axis of the cone and reaches an observer perpendicular to the ray out of the paper. It is a cone in 3D in the first place.
And this accounts for a reflected ray, even when \(\alpha_2\) does not penetrate into the second medium.
Note: The cone \(PE^{'}\,\,E\,\,PE\) was not initially conceived from considering absorption and emission. There can be a problem here; two birds with one stone is real luck! The cone accounts for both the direction along the ray and, emitted photons that reach the eyes of the observer, perpendicular to the ray.
Both ray \(-\alpha_2\) and \(90^o-\theta_2-\alpha_2\) are at the point of incident, very small.
\(E_{p}=h.\left\{1-\sqrt{\cfrac{sin(\theta)}{cos(\theta)}}\right\}.f_{cir}\)
when
\(1-\sqrt{\cfrac{sin(\theta)}{cos(\theta)}}\lt0\)
\(\sqrt{\cfrac{sin(\theta)}{cos(\theta)}}\gt1\)
a photon is absorbed first then emitted, this introduces a \(\small{\pi}\) phase in the emission.
The refracted ray we observe in the second medium is made up of emitted photons in the direction perpendicular to \(\alpha_2\) (out of the paper). This emitted ray will be absorbed and be emitted a second time. In the first instance of emission, the photons are emitted perpendicular to the direction of travel of the particle (\(P^{'}O\) and \(PO\)), and is along \(E\,\,PE^{'}\) and \(E\,\,PE\). The direction of incident then changes to from \(PO\) to \(EO\), by a difference of \(90^o-\theta\). Along \(EO\) particles interact with the passing photons, as if along \(PO\).
The ray \(\alpha_2\) corresponds to the line \(EO\). \(EO\) is absorbed and emitted into the direction it was first absorbed. It is diverted by a difference of \(-(90^o-\theta)\) to be along \(PO\) again. Reciprocity.
If we confine photon emission/absorption to be at the point of incident, this emitted ray, \(PO\) will result in a reflected ray,
And the possibility of a phase lag between the absorption of a photon first, then an emission, accounts for the possible \(\pi\) phase shift in the reflected ray.
This is not the reflected ray off a mirrored surface, but reflection from an interface of two mediums with different optical properties. The reflected ray is the result of a second absorption/emission of the photons in the medium, the first absorption/emission allows us to see \(\alpha_2\). The second absorption/emission is due to the interaction of \(\alpha_2\) with the medium. \(\alpha_2\) interacts with the medium only once. The first absorption/emission of the photons in the medium results in the cone \(PE^{'}\,\,E\,\,PE\) from which we started to derive the geometry of \(\alpha_2\) (post "It's All Fluorescence Outside, Inside" dated 29 Jul 2015).
The ray corresponding to \(90^o-\theta_2-\alpha_2\) is probably totally internally reflected. The presence of this ray is important to vindicate the results here. It is possible that not all of this ray is absorbed and emitted to result in a reflected ray.
When would absorption and emission stop? Absorb along \(AB\) \(\to\) emit perpendicularly \(XY\) \(\to\) absorb along \(XY\) \(\to\) emit perpendicularly along \(AB\), return. The photons are emitted in the direction perpendicular to the particle's travel; this is not in the direction perpendicular to the ray on the plane containing the axis of the cone. This emitted ray is rotated about the axis of the cone and reaches an observer perpendicular to the ray out of the paper. It is a cone in 3D in the first place.
And this accounts for a reflected ray, even when \(\alpha_2\) does not penetrate into the second medium.
Note: The cone \(PE^{'}\,\,E\,\,PE\) was not initially conceived from considering absorption and emission. There can be a problem here; two birds with one stone is real luck! The cone accounts for both the direction along the ray and, emitted photons that reach the eyes of the observer, perpendicular to the ray.
Both ray \(-\alpha_2\) and \(90^o-\theta_2-\alpha_2\) are at the point of incident, very small.
Tuesday, August 18, 2015
Once Again Brewster
On closer look at the situation when \(\alpha_{2s}\) and \(\alpha_{2p}\) are perpendicular,
In the second medium,
\(2\theta_1-\Delta\theta-\Delta\alpha=90^o\)
where,
\(\Delta\theta=\theta_1-\theta_2\)
\(\Delta\alpha=\alpha_1-\alpha_2\)
which implies \(2\theta_1\gt90^o\) and so, \(\theta_1\gt45^o\)
So,
\(\theta_1+\theta_2-\alpha_1+\alpha_2=90^o\)
both material properties \(\varepsilon\) and \(n\) are involved. Alternatively,
\(2\theta_1-90^o=\Delta\theta+\Delta\alpha\)
the change in orientation needed, is from both a change in \(\theta\) and \(\alpha\).
When we set,
\(\alpha_1=\theta_1\) --- (1)
then,
\(\theta_2+\alpha_2=90^o\) --- (2)
the ray splits into two perpendicular directions with orthogonal polarization. Given a light source with a spread of values in \(\theta\), there can be a number of \(\theta\) for which a split of the refracted rays orthogonal to each other can occur. Expressions (1) and (2) are the same as those we obtained in the post "Still Looking For Brewster" dated 16 Aug 2015. From that post,
\({ tan(\alpha_1)}{tan(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(\cfrac{ sin^2(\alpha_1)}{cos(\alpha_1)cos(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\)
but \(\alpha_1+\alpha_2\ne90^o\) as oppose to the often quoted \(\alpha_1+\alpha_2=90^o\) in the derivation for Brewster's angle. Instead,
\(sin(\alpha_2)=\cfrac{n_1}{n_2}sin(\alpha_1)\)
\(cos(\alpha_2)=\sqrt{1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)}\)
So,
\(tan(\alpha_1).\cfrac{n_1}{n_2}\cfrac{sin(\alpha_1)}{\sqrt{1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)}}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(tan^2(\alpha_1)sin^2(\alpha_1)=\left(\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\right)^2\left\{1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)\right\}\)
\(tan^2(\alpha_1)sin^2(\alpha_1)+\left(\cfrac{\varepsilon_2}{\varepsilon_1}\right)^2sin^2(\alpha_1)=\left(\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\right)^2\)
In the second medium,
\(2\theta_1-\Delta\theta-\Delta\alpha=90^o\)
where,
\(\Delta\theta=\theta_1-\theta_2\)
\(\Delta\alpha=\alpha_1-\alpha_2\)
which implies \(2\theta_1\gt90^o\) and so, \(\theta_1\gt45^o\)
So,
\(\theta_1+\theta_2-\alpha_1+\alpha_2=90^o\)
both material properties \(\varepsilon\) and \(n\) are involved. Alternatively,
\(2\theta_1-90^o=\Delta\theta+\Delta\alpha\)
the change in orientation needed, is from both a change in \(\theta\) and \(\alpha\).
When we set,
\(\alpha_1=\theta_1\) --- (1)
then,
\(\theta_2+\alpha_2=90^o\) --- (2)
the ray splits into two perpendicular directions with orthogonal polarization. Given a light source with a spread of values in \(\theta\), there can be a number of \(\theta\) for which a split of the refracted rays orthogonal to each other can occur. Expressions (1) and (2) are the same as those we obtained in the post "Still Looking For Brewster" dated 16 Aug 2015. From that post,
\({ tan(\alpha_1)}{tan(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(\cfrac{ sin^2(\alpha_1)}{cos(\alpha_1)cos(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\)
but \(\alpha_1+\alpha_2\ne90^o\) as oppose to the often quoted \(\alpha_1+\alpha_2=90^o\) in the derivation for Brewster's angle. Instead,
\(sin(\alpha_2)=\cfrac{n_1}{n_2}sin(\alpha_1)\)
\(cos(\alpha_2)=\sqrt{1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)}\)
So,
\(tan(\alpha_1).\cfrac{n_1}{n_2}\cfrac{sin(\alpha_1)}{\sqrt{1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)}}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(tan^2(\alpha_1)sin^2(\alpha_1)=\left(\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\right)^2\left\{1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)\right\}\)
\(tan^2(\alpha_1)sin^2(\alpha_1)+\left(\cfrac{\varepsilon_2}{\varepsilon_1}\right)^2sin^2(\alpha_1)=\left(\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\right)^2\)
\(sin^4(\alpha_1)+\left(\cfrac{\varepsilon_2}{\varepsilon_1}\right)^2sin^2(\alpha_1)(1-sin^2(\alpha_1))=\left(\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\right)^2(1-sin^2(\alpha_1))\)
\(sin^{ 4 }(\alpha _{ 1 })+\left( \cfrac { \varepsilon _{ 2 } }{ \varepsilon _{ 1 } } \right) ^{ 2 }sin^{ 2 }(\alpha _{ 1 })-\left( \cfrac { \varepsilon _{ 2 } }{ \varepsilon _{ 1 } } \right) ^{ 2 }sin^{ 4 }(\alpha _{ 1 })=\left( \cfrac { \varepsilon _{ 2 } }{ \varepsilon _{ 1 } } \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 }-\left( \cfrac { \varepsilon _{ 2 } }{ \varepsilon _{ 1 } } \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 }sin^{ 2 }(\alpha _{ 1 })\)
\( sin^{ 4 }(\alpha _{ 1 })\left\{ 1-\left( \cfrac { \varepsilon _{ 2 } }{ \varepsilon _{ 1 } } \right) ^{ 2 } \right\} +\left( \cfrac { \varepsilon _{ 2 } }{ \varepsilon _{ 1 } } \right) ^{ 2 }\left\{ 1+\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 } \right\} sin^{ 2 }(\alpha _{ 1 })=\left( \cfrac { \varepsilon _{ 2 } }{ \varepsilon _{ 1 } } \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 }\)
\(sin^{ 4 }(\alpha _{ 1 })\left\{ \left( \cfrac { \varepsilon _{ 1 } }{ \varepsilon _{ 2 } } \right) ^{ 2 }-1 \right\} +\left\{ 1+\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 } \right\} sin^{ 2 }(\alpha _{ 1 })=\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 }\)
\(sin^{ 4 }(\alpha _{ 1 })\left\{ \left( \cfrac { \varepsilon _{ 1 } }{ \varepsilon _{ 2 } } \right) ^{ 2 }-1 \right\} +\left\{ 1+\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 } \right\} sin^{ 2 }(\alpha _{ 1 })=\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 }\)
which is quadratic in \(sin^2(\alpha_1)\) and can yield two positive solutions for \(\alpha_1\).
When \(\cfrac { \varepsilon _{ 2 } }{ \varepsilon _{ 1 } }=1\),
\(\left\{ 1+\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 } \right\} sin^{ 2 }(\alpha _{ 1 })=\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 }\)
\(sin^{ 2 }(\alpha _{ 1 })=\frac { \left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 } }{ \left\{ 1+\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 } \right\} }\)
\(tan(\alpha_1)=\cfrac{n_2}{n_1}\)
and this Brewster!
Thank you very much.
When \(\cfrac { \varepsilon _{ 2 } }{ \varepsilon _{ 1 } }=1\),
\(\left\{ 1+\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 } \right\} sin^{ 2 }(\alpha _{ 1 })=\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 }\)
\(sin^{ 2 }(\alpha _{ 1 })=\frac { \left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 } }{ \left\{ 1+\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 } \right\} }\)
and this Brewster!
Thank you very much.
Monday, August 17, 2015
Does Not Look Like What?
From the post "A Bloom Crosses Over" dated 10 Aug 2015,
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(\varepsilon_2\gt\varepsilon_1\)
then,
\(\theta_2\lt\theta_1\)
\(\Delta\theta=\theta_2-\theta_1\lt0\)
In all the previous diagrams \(\Delta\theta\gt0\).
If \(\Delta\theta^{\,'}=-\Delta\theta\)
where \(\varepsilon_2\gt\varepsilon_1\).
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(\varepsilon_2\gt\varepsilon_1\)
then,
\(\theta_2\lt\theta_1\)
\(\Delta\theta=\theta_2-\theta_1\lt0\)
In all the previous diagrams \(\Delta\theta\gt0\).
If \(\Delta\theta^{\,'}=-\Delta\theta\)
where \(\varepsilon_2\gt\varepsilon_1\).
Sunday, August 16, 2015
Still Looking For Brewster
From the post "Late Bloomer Gets The Splits" dated 10 Aug 2015,
\(B_1sin(\alpha_{adj\,\,1})=B_2sin(\alpha_{adj\,\,2})\)
\(\cfrac{B_1}{\mu_1}cos(\alpha_{adj\,\,1})=\cfrac{B_2}{\mu_2}cos(\alpha_{adj\,\,2})\)
\(\alpha_{adj\,\,1}=90^o+\alpha_1-\theta_1\)
\(\alpha_{adj\,\,2}=90^o+\alpha_2-\theta_2\)
but when,
\(\alpha_1=\theta_1\)
\(cos(\alpha_{adj\,\,1})=cos(90^o)=0\)
or when,
\(\alpha_2=\theta_2\)
\(cos(\alpha_{adj\,\,2})=cos(90^o)=0\)
in which case,
\(\mu_1tan(\alpha _{adj\,\, 1 })=\mu_2tan(\alpha _{adj\,\, 2 })\)
is not valid,
The tangential component of the incident ray is zero and the ray enters the medium perpendicular to the inter-surface, parallel to the normal. \(\alpha_{2s}\) passes through the second medium perpendicularly.
In a similar way, when we consider the left arm,
\(B_1sin(\alpha_{adj\,\,1})=B_2sin(\alpha_{adj\,\,2})\)
\(\cfrac{B_1}{\mu_1}cos(\alpha_{adj\,\,1})=\cfrac{B_2}{\mu_2}cos(\alpha_{adj\,\,2})\)
\(\alpha_{adj\,\,1}=\theta_1+\alpha_1-90^o\)
in the first medium, and into the second medium,
\(\alpha_{adj\,\,2}=\theta_2+\alpha_2-90^o\)
If \(\theta_1+\alpha_1=90^o\)
\(sin(\alpha_{adj\,\,1})=sin(0^o)=0\)
or when,
\(B_1sin(\alpha_{adj\,\,1})=B_2sin(\alpha_{adj\,\,2})\)
\(\cfrac{B_1}{\mu_1}cos(\alpha_{adj\,\,1})=\cfrac{B_2}{\mu_2}cos(\alpha_{adj\,\,2})\)
\(\alpha_{adj\,\,1}=90^o+\alpha_1-\theta_1\)
\(\alpha_{adj\,\,2}=90^o+\alpha_2-\theta_2\)
but when,
\(\alpha_1=\theta_1\)
\(cos(\alpha_{adj\,\,1})=cos(90^o)=0\)
or when,
\(\alpha_2=\theta_2\)
\(cos(\alpha_{adj\,\,2})=cos(90^o)=0\)
in which case,
\(\mu_1tan(\alpha _{adj\,\, 1 })=\mu_2tan(\alpha _{adj\,\, 2 })\)
is not valid,
The tangential component of the incident ray is zero and the ray enters the medium perpendicular to the inter-surface, parallel to the normal. \(\alpha_{2s}\) passes through the second medium perpendicularly.
In a similar way, when we consider the left arm,
\(B_1sin(\alpha_{adj\,\,1})=B_2sin(\alpha_{adj\,\,2})\)
\(\cfrac{B_1}{\mu_1}cos(\alpha_{adj\,\,1})=\cfrac{B_2}{\mu_2}cos(\alpha_{adj\,\,2})\)
in the first medium, and into the second medium,
\(\alpha_{adj\,\,2}=\theta_2+\alpha_2-90^o\)
If \(\theta_1+\alpha_1=90^o\)
\(sin(\alpha_{adj\,\,1})=sin(0^o)=0\)
or when,
\(\theta_2+\alpha_2=90^o\)
\(sin(\alpha_{adj\,\,2})=sin(0^o)=0\)
\(sin(\alpha_{adj\,\,2})=sin(0^o)=0\)
the perpendicular component of the left incident arm is zero. The tangential component \(\alpha_{2p}\), glides along the surface (if it is flat) and does not enter the second medium.
Both scenario occurs when,
\(\theta_1=\alpha_1\)
and
\(\theta_2+\alpha_2=90^o\)
The incident ray is split \(90^o\) one along the surface \(\alpha_{2p}\), and the other enters the second medium perpendicularly \(\alpha_{2s}\). This is wrong, velocity along the ray was not accounted for.
This is still not Brewster angle. But, from
\(\theta_2+\alpha_2=90^o\)
\(\theta_2=90^o-\alpha_2\)
\(\theta_1=\alpha_1\)
Since, from the post "A Bloom Crosses Over" dated 10 Aug 2015,
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(\cfrac{ tan(\alpha_1)}{tan(90^o-\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\({ tan(\alpha_1)}{tan(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
From Snell's Law,
\(n_1sin(\alpha_1)=n_2sin(\alpha_2)\)
\(\cfrac{n_1}{n_2}\cfrac{ sin^2(\alpha_1)}{cos(\alpha_1)cos(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
and
\(\cfrac{ sin^2(\alpha_1)}{cos(\alpha_1)cos(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\)
\(\alpha_1+\alpha_2=90^o\) This is wrong!
\(\cfrac{ sin^2(\alpha_1)}{cos(\alpha_1)cos(90^o-\alpha_1)}=\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\)
\(\cfrac{ sin(\alpha_1)}{cos(\alpha_1)}=tan(\alpha_1)=\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\)
which is still not Brewster.
Both scenario occurs when,
\(\theta_1=\alpha_1\)
and
\(\theta_2+\alpha_2=90^o\)
The incident ray is split \(90^o\) one along the surface \(\alpha_{2p}\), and the other enters the second medium perpendicularly \(\alpha_{2s}\). This is wrong, velocity along the ray was not accounted for.
This is still not Brewster angle. But, from
\(\theta_2+\alpha_2=90^o\)
\(\theta_2=90^o-\alpha_2\)
\(\theta_1=\alpha_1\)
Since, from the post "A Bloom Crosses Over" dated 10 Aug 2015,
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(\cfrac{ tan(\alpha_1)}{tan(90^o-\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\({ tan(\alpha_1)}{tan(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
From Snell's Law,
\(n_1sin(\alpha_1)=n_2sin(\alpha_2)\)
\(\cfrac{n_1}{n_2}\cfrac{ sin^2(\alpha_1)}{cos(\alpha_1)cos(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
and
\(\cfrac{ sin^2(\alpha_1)}{cos(\alpha_1)cos(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\)
\(\alpha_1+\alpha_2=90^o\) This is wrong!
\(\cfrac{ sin^2(\alpha_1)}{cos(\alpha_1)cos(90^o-\alpha_1)}=\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\)
\(\cfrac{ sin(\alpha_1)}{cos(\alpha_1)}=tan(\alpha_1)=\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\)
which is still not Brewster.
Looking for Brewster
When we consider,
\(tan(\theta_2-\alpha^{'}_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha)\)
when \(\theta_1\) is large, such that
\(\theta_1-\alpha\gt90^o\)
Let \(x+90^o=\theta_1-\alpha\) then
\(tan(\theta_1-\alpha)=tan(x+90^o)=-cot(x)\)
So,
\(tan(\theta_2-\alpha^{'}_{2s})=-\cfrac{\mu_2}{\mu_1}cot(\theta_1-\alpha-90^o)\)
\(cot(\theta_2-\alpha^{'}_{2s}+90^o)=\cfrac{\mu_2}{\mu_1}cot(\theta_1-\alpha-90^o)\)
When \(\mu _{ 2 }\gt\mu _{ 1 }\), since \(cot(x)\) is a decreasing function,
\(\theta_2-\alpha^{'}_{2s}+90^o\lt\theta_1-\alpha-90^o\)
\(\alpha^{'}_{2s}\gt180^o+\alpha+\Delta \theta\)
Since the \(\alpha^{'}_{2s}\) has been reflected back into medium 1, \(\Delta \theta=0\),
\(\alpha^{'}_{2s}\gt180^o+\alpha\)
When \(\mu _{ 2 }\lt\mu _{ 1 }\),
\(\theta_2-\alpha^{'}_{2s}+90^o\gt\theta_1-\alpha-90^o\)
\(\alpha^{'}_{2s}\lt180^o+\alpha\)
\(tan(\theta_2+\alpha^{'}_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha)\)
when \(\theta_1\) is large, such that
\(\theta_1+\alpha\gt90^o\)
Let \(x+90^o=\theta_1+\alpha\) then
\(tan(\theta_1+\alpha)=tan(x+90^o)=-cot(x)\)
So,
\(tan(\theta_2+\alpha^{'}_{2p})=-\cfrac{\mu_2}{\mu_1}cot(\theta_1+\alpha-90^o)\)
\(cot(\theta_2+\alpha^{'}_{2p}+90^o)=\cfrac{\mu_2}{\mu_1}cot(\theta_1+\alpha-90^o)\)
When \(\mu _{ 2 }\gt\mu _{ 1 }\),
\(\theta_2+\alpha^{'}_{2p}+90^o\lt\theta_1+\alpha-90^o\)
\(\alpha^{'}_{2p}\lt\alpha-\Delta\theta-180^o\)
Since, \(\Delta\theta=0\)
\(\alpha^{'}_{2p}\) is reflected back along \(\alpha\)
When \(\mu _{ 2 }\lt\mu _{ 1 }\),
\(\theta_2+\alpha^{'}_{2p}+90^o\gt\theta_1+\alpha-90^o\)
\(\alpha^{'}_{2p}\gt\alpha-\Delta\theta-180^o\)
Since, \(\Delta\theta=0\)
When \(\mu _{ 2 }\lt\mu _{ 1 }\), \(\alpha^{'}_{2s}\lt180^o+\alpha\)
When \(\mu _{ 2 }\gt\mu _{ 1 }\), \(\alpha^{'}_{2p}\lt\alpha-180^o\)
When \(\mu _{ 2 }\lt\mu _{ 1 }\), \(\alpha^{'}_{2p}\gt\alpha-180^o\)
\(tan(\theta_2-\alpha^{'}_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha)\)
when \(\theta_1\) is large, such that
\(\theta_1-\alpha\gt90^o\)
Let \(x+90^o=\theta_1-\alpha\) then
\(tan(\theta_1-\alpha)=tan(x+90^o)=-cot(x)\)
So,
\(tan(\theta_2-\alpha^{'}_{2s})=-\cfrac{\mu_2}{\mu_1}cot(\theta_1-\alpha-90^o)\)
\(cot(\theta_2-\alpha^{'}_{2s}+90^o)=\cfrac{\mu_2}{\mu_1}cot(\theta_1-\alpha-90^o)\)
When \(\mu _{ 2 }\gt\mu _{ 1 }\), since \(cot(x)\) is a decreasing function,
\(\theta_2-\alpha^{'}_{2s}+90^o\lt\theta_1-\alpha-90^o\)
\(\alpha^{'}_{2s}\gt180^o+\alpha+\Delta \theta\)
Since the \(\alpha^{'}_{2s}\) has been reflected back into medium 1, \(\Delta \theta=0\),
\(\alpha^{'}_{2s}\gt180^o+\alpha\)
When \(\mu _{ 2 }\lt\mu _{ 1 }\),
\(\theta_2-\alpha^{'}_{2s}+90^o\gt\theta_1-\alpha-90^o\)
\(\alpha^{'}_{2s}\lt180^o+\alpha\)
We can also have,
\(tan(\theta_2+\alpha^{'}_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha)\)
when \(\theta_1\) is large, such that
\(\theta_1+\alpha\gt90^o\)
Let \(x+90^o=\theta_1+\alpha\) then
\(tan(\theta_1+\alpha)=tan(x+90^o)=-cot(x)\)
So,
\(tan(\theta_2+\alpha^{'}_{2p})=-\cfrac{\mu_2}{\mu_1}cot(\theta_1+\alpha-90^o)\)
\(cot(\theta_2+\alpha^{'}_{2p}+90^o)=\cfrac{\mu_2}{\mu_1}cot(\theta_1+\alpha-90^o)\)
When \(\mu _{ 2 }\gt\mu _{ 1 }\),
\(\theta_2+\alpha^{'}_{2p}+90^o\lt\theta_1+\alpha-90^o\)
\(\alpha^{'}_{2p}\lt\alpha-\Delta\theta-180^o\)
Since, \(\Delta\theta=0\)
\(\alpha^{'}_{2p}\lt\alpha-180^o\)
When \(\mu _{ 2 }\lt\mu _{ 1 }\),
\(\theta_2+\alpha^{'}_{2p}+90^o\gt\theta_1+\alpha-90^o\)
\(\alpha^{'}_{2p}\gt\alpha-\Delta\theta-180^o\)
Since, \(\Delta\theta=0\)
\(\alpha^{'}_{2p}\gt\alpha-180^o\)
This might seem to be the same results as the post "More Bending Of Light" dated 13 Aug 2015, but the swing of \(\alpha_s\) and \(\alpha_p\) are different,
When \(\mu _{ 2 }\gt\mu _{ 1 }\), \(\alpha^{'}_{2s}\gt180^o+\alpha\)
When \(\mu _{ 2 }\lt\mu _{ 1 }\), \(\alpha^{'}_{2p}\gt\alpha-180^o\)
Previously,
When \(\mu_2\gt\mu_1\), \(\alpha_{2s}\lt-180^o+\alpha\)
When \(\mu_2\lt\mu_1\), \(\alpha_{2s}\gt-180^o+\alpha\)
This cases show the swing of \(\alpha_{2s}\) and \(\alpha_{2p}\) as \(\theta_1\) changed. There is no Brewster angle here.
Decreasing Polarization Was Common Sense
Ooops,
The angle was assigned wrongly in the post "A Bloom Crosses Over" dated 10 Aug 2015.
It should have been,
\(\beta=90^o-\theta\)
and so,
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
as the cone spreads, \(\beta\) increases but \(\theta\) decreases. And when,
\(\varepsilon_1\lt\varepsilon_2\)
\(\theta_1\gt\theta_2\)
polarization decreases.
This is then consistent with post "On Reflection Radar Theory 101" dated 16 Aug 2015, where the horizontal component of \(E\) attenuates and \(\theta\) decreases.
Which proves common sense is rare.
The angle was assigned wrongly in the post "A Bloom Crosses Over" dated 10 Aug 2015.
It should have been,
\(\beta=90^o-\theta\)
and so,
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
as the cone spreads, \(\beta\) increases but \(\theta\) decreases. And when,
\(\varepsilon_1\lt\varepsilon_2\)
\(\theta_1\gt\theta_2\)
polarization decreases.
This is then consistent with post "On Reflection Radar Theory 101" dated 16 Aug 2015, where the horizontal component of \(E\) attenuates and \(\theta\) decreases.
Which proves common sense is rare.
On Reflection Radar Theory 101
From the post "Turning With The Rest Of Us" and "More Bending Of Light" both dated 13 Aug 2015, when
\(\theta_1-\alpha\lt0\)
For \(\mu_2\lt\mu_1\),
\(\alpha_{2s}\gt-180^o+\alpha\)
and \(\mu_2\gt\mu_1\),
\(\alpha_{2s}\lt-180^o+\alpha\)
The reflected ray, \(\alpha_{2s}\) can be steered by changing \(\mu_2\),
\(tan(\theta_2-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha)\)
\(\alpha_{2s}\) being reflected by rotating \(-180^o\).
\(\theta_1=\theta_2\)
\(tan(\theta_1-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha)\)
This is important in the case of \(EMW\) where a reflector opposite to an emitting source focuses the radiation behind the source.
In the case of a perfect conductor, \(\alpha_{2p}\) does not exist as there cannot be magnetic fields inside the conductor. \(\alpha_{2p}\) is absorbed by the conductor; half of the energy in the wave is absorbed. If \(\theta\) is kept small, the vertical component of the \(E\) field is small compared to the horizontal component in the direction of travel of the radiation. This horizontal component attenuates as the wave move into medium of varying \(\varepsilon\); the vertical component remained unchanged. \(\theta\) should be kept large \(\theta\to90^o\) as \(\alpha_{2s}\) only depends on \(\alpha\), \(\mu_2\) and \(\mu_1\), up to the range over which the horizontal component of \(E\) attenuates completely. As the wave attenuates, \(\theta\) decreases and is more readily reflected given the incident angle \(\alpha\).
Apart from keeping polarization high, \(\Delta\theta\) dose not effect \(\alpha_{2s}\), the reflected EMW.
\(\theta_1-\alpha\lt0\)
For \(\mu_2\lt\mu_1\),
\(\alpha_{2s}\gt-180^o+\alpha\)
and \(\mu_2\gt\mu_1\),
\(\alpha_{2s}\lt-180^o+\alpha\)
The reflected ray, \(\alpha_{2s}\) can be steered by changing \(\mu_2\),
\(tan(\theta_2-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha)\)
\(\alpha_{2s}\) being reflected by rotating \(-180^o\).
\(\theta_1=\theta_2\)
\(tan(\theta_1-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha)\)
This is important in the case of \(EMW\) where a reflector opposite to an emitting source focuses the radiation behind the source.
In the case of a perfect conductor, \(\alpha_{2p}\) does not exist as there cannot be magnetic fields inside the conductor. \(\alpha_{2p}\) is absorbed by the conductor; half of the energy in the wave is absorbed. If \(\theta\) is kept small, the vertical component of the \(E\) field is small compared to the horizontal component in the direction of travel of the radiation. This horizontal component attenuates as the wave move into medium of varying \(\varepsilon\); the vertical component remained unchanged. \(\theta\) should be kept large \(\theta\to90^o\) as \(\alpha_{2s}\) only depends on \(\alpha\), \(\mu_2\) and \(\mu_1\), up to the range over which the horizontal component of \(E\) attenuates completely. As the wave attenuates, \(\theta\) decreases and is more readily reflected given the incident angle \(\alpha\).
Apart from keeping polarization high, \(\Delta\theta\) dose not effect \(\alpha_{2s}\), the reflected EMW.
Friday, August 14, 2015
Old Friends
If \(\mu\) is to \(B\) as \(\varepsilon\) is to \(E\), what then is \(n\) to? Why, in the first place photons reduce velocity?
\(v^2=\cfrac{1}{\mu\varepsilon}\)
\(\cfrac{v^2_1}{v^2_2}=\cfrac{\mu_2\varepsilon_2}{\mu_1\varepsilon_1}\)
Since,
\(c^2=\cfrac{1}{\mu_o\varepsilon_o}\)
If we define,
\(n_o=\sqrt{\mu_o\varepsilon_o}\)
then,
\(n_r=\cfrac{n}{n_o}=\sqrt{\cfrac{\mu\varepsilon}{\mu_o\varepsilon_o}}\)
\(n_r=\cfrac{1}{v\sqrt{\mu_o\varepsilon_o}}\)
\(n_r.v=c\)
\(n\) is the result of both \(\mu\) on \(B\) and \(\varepsilon\) on \(E\). \(n_r\) is defined relative to \(c\), or \(\small{\sqrt{\mu_o\varepsilon_o}}\)
\(v^2=\cfrac{1}{\mu\varepsilon}\)
\(\cfrac{v^2_1}{v^2_2}=\cfrac{\mu_2\varepsilon_2}{\mu_1\varepsilon_1}\)
Since,
\(c^2=\cfrac{1}{\mu_o\varepsilon_o}\)
If we define,
\(n_o=\sqrt{\mu_o\varepsilon_o}\)
then,
\(n_r=\cfrac{n}{n_o}=\sqrt{\cfrac{\mu\varepsilon}{\mu_o\varepsilon_o}}\)
\(n_r=\cfrac{1}{v\sqrt{\mu_o\varepsilon_o}}\)
\(n_r.v=c\)
\(n\) is the result of both \(\mu\) on \(B\) and \(\varepsilon\) on \(E\). \(n_r\) is defined relative to \(c\), or \(\small{\sqrt{\mu_o\varepsilon_o}}\)
Thursday, August 13, 2015
Turning With The Rest Of Us?
Cont'd from the previous post "More Bending of Light",
When we superimpose the effect of refraction, is \(\alpha_{2s}\) in the first medium along \(\alpha_1\) or along \(\alpha_2\) rotated by \(180^o\)?
In the second medium, \(\alpha_2\) is rotated.
When we superimpose the effect of refraction, is \(\alpha_{2s}\) in the first medium along \(\alpha_1\) or along \(\alpha_2\) rotated by \(180^o\)?
In the second medium, \(\alpha_2\) is rotated.
More Bending Of Light
From the post "Split Cannot Mend" dated 10 Aug 2015,
\(tan(\theta_2-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha)\)
when
\(\theta_1-\alpha\lt0\)
ie incident angle \(\alpha\) large,
\(tan(\theta_2-\alpha_{2s})=-\cfrac{\mu_2}{\mu_1}tan(\alpha-\theta_1)\)
\(tan(\theta_2-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(180^o-\alpha+\theta_1)\)
When \(\mu_2\lt\mu_1\),
\(\theta_2-\alpha_{2s}\lt180^o-\alpha+\theta_1\)
\(\alpha_{2s}\gt\Delta \theta-180^o+\alpha\)
But if \(\alpha_{2s}\) is to make a turn of \(-180^o\),
\(\theta_2=\theta_1\)
\(\Delta \theta=0\)
And so,
\(\alpha_{2s}\gt-180^o+\alpha\)
Also consider when \(\mu_2\gt\mu_1\),
\(\theta_2-\alpha_{2s}\gt180^o-\alpha+\theta_1\)
\(\alpha_{2s}\lt\Delta \theta-180^o+\alpha\)
But if \(\alpha_{2s}\) is to make a turn of \(-180^o\),
\(\theta_2=\theta_1\)
\(\Delta \theta=0\)
And so,
\(\alpha_{2s}\lt-180^o+\alpha\)
So, when \(\mu_2=\mu_1\)
\(\alpha_{2s}=-180^o+\alpha\)
\(\alpha_{2s}\) is reflected back along \(\alpha\), as \(\alpha_{2s}\) is measured anticlockwise positive. In all cases, \(\alpha_{2s}\) is reflected back into in medium \(\mu_1\).
When we consider,
\(tan(\theta_2+\alpha_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha)\)
for large incident angle \(\alpha\), such that
\(\theta_1+\alpha\gt180^o\)
This happens with \(\small{EMW}\) where \(\theta\) is measured towards the positive \(E\) direction.
Let \(x+180^o=\theta_1+\alpha\) then
\(tan(\theta_1+\alpha)=tan(x+180^o)=tan(x)\)
So,
\(tan(\theta_2+\alpha_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha-180^o)\)
\(tan(180^o+\theta_2+\alpha_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha-180^o)\)
When \(\mu_2\lt\mu_1\),
\(180^o+\theta_2+\alpha_{2p}\lt\theta_1+\alpha-180^o\)
\(\alpha_{2p}\lt-360^o-\Delta\theta+\alpha\)
and when \(\mu_2\gt\mu_1\),
\(180^o+\theta_2+\alpha_{2p}\gt\theta_1+\alpha-180^o\)
\(\alpha_{2p}\gt-360^o-\Delta\theta+\alpha\)
In these cases, \(\alpha_{2p}\) is not in the same medium.
The two beams \(\alpha_{2s}\) and \(\alpha_{2p}\) behave differently for large incident angle \(\alpha\). \(\alpha_{2s}\) is reflected back along \(\alpha\), the incident ray and \(\alpha_{2p}\) is displaced from the extrapolated path of \(\alpha\) by \(-\Delta \theta\).
Total internal reflection due to velocity changes as photons pass through the two mediums is a distinct phenomenon apart from these.
\(tan(\theta_2-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha)\)
when
\(\theta_1-\alpha\lt0\)
ie incident angle \(\alpha\) large,
\(tan(\theta_2-\alpha_{2s})=-\cfrac{\mu_2}{\mu_1}tan(\alpha-\theta_1)\)
\(tan(\theta_2-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(180^o-\alpha+\theta_1)\)
When \(\mu_2\lt\mu_1\),
\(\theta_2-\alpha_{2s}\lt180^o-\alpha+\theta_1\)
\(\alpha_{2s}\gt\Delta \theta-180^o+\alpha\)
But if \(\alpha_{2s}\) is to make a turn of \(-180^o\),
\(\theta_2=\theta_1\)
\(\Delta \theta=0\)
And so,
\(\alpha_{2s}\gt-180^o+\alpha\)
Also consider when \(\mu_2\gt\mu_1\),
\(\theta_2-\alpha_{2s}\gt180^o-\alpha+\theta_1\)
\(\alpha_{2s}\lt\Delta \theta-180^o+\alpha\)
But if \(\alpha_{2s}\) is to make a turn of \(-180^o\),
\(\theta_2=\theta_1\)
\(\Delta \theta=0\)
And so,
\(\alpha_{2s}\lt-180^o+\alpha\)
So, when \(\mu_2=\mu_1\)
\(\alpha_{2s}=-180^o+\alpha\)
\(\alpha_{2s}\) is reflected back along \(\alpha\), as \(\alpha_{2s}\) is measured anticlockwise positive. In all cases, \(\alpha_{2s}\) is reflected back into in medium \(\mu_1\).
\(tan(\theta_2+\alpha_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha)\)
for large incident angle \(\alpha\), such that
\(\theta_1+\alpha\gt180^o\)
This happens with \(\small{EMW}\) where \(\theta\) is measured towards the positive \(E\) direction.
Let \(x+180^o=\theta_1+\alpha\) then
\(tan(\theta_1+\alpha)=tan(x+180^o)=tan(x)\)
So,
\(tan(\theta_2+\alpha_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha-180^o)\)
\(tan(180^o+\theta_2+\alpha_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha-180^o)\)
When \(\mu_2\lt\mu_1\),
\(180^o+\theta_2+\alpha_{2p}\lt\theta_1+\alpha-180^o\)
\(\alpha_{2p}\lt-360^o-\Delta\theta+\alpha\)
\(180^o+\theta_2+\alpha_{2p}\gt\theta_1+\alpha-180^o\)
\(\alpha_{2p}\gt-360^o-\Delta\theta+\alpha\)
In these cases, \(\alpha_{2p}\) is not in the same medium.
The two beams \(\alpha_{2s}\) and \(\alpha_{2p}\) behave differently for large incident angle \(\alpha\). \(\alpha_{2s}\) is reflected back along \(\alpha\), the incident ray and \(\alpha_{2p}\) is displaced from the extrapolated path of \(\alpha\) by \(-\Delta \theta\).
Total internal reflection due to velocity changes as photons pass through the two mediums is a distinct phenomenon apart from these.
Wednesday, August 12, 2015
All Mathematical Interpretations Are Fiction
Consider the \(\psi\) of a particle expanding from \(x=x_a\) to \(x=x_c\), \(\psi\) is at velocity \(c\) along \(ix\), the gain in energy is,
\(\Delta E=E_{x_c}-E_{x_a}=2\pi x_cmc-2\pi x_amc\)
But,
\(\Delta E=\bar F.\Delta x=2\pi mc(x_c-x_a)\)
so,
\(\bar F=2\pi mc\)
We know that,
\(F=-\psi\)
where \(F\) the Newtonian force due to \(\psi\). The average force on \(\psi\) is,
\(\bar F =-(-\bar \psi)=\bar\psi=2\pi mc\)
as the particle's \(\psi\) expanded from \(x_a\) to \(x_c\). Through out this process \(KE=\cfrac{1}{2}mc^2\) remains unchanged.
The average acceleration,
\(\bar a_c=2\pi c\)
Since the particle is in circular motion, and \(\bar F\) is along a radial line,
\(\bar F=2\pi c=\cfrac{c^2}{\bar x}\)
and
\(\bar x=\cfrac{c}{2\pi}\)
What is \(\bar x\)? \(\bar F\) is a hypothetical average force, that extends up to \(\bar x\) and is zero beyond. But be warned, all mathematical interpretations are fiction next to bullshit. Bullshit on the other hand, bulls will testify, is for real.
Have a nice day.
\(\Delta E=E_{x_c}-E_{x_a}=2\pi x_cmc-2\pi x_amc\)
But,
\(\Delta E=\bar F.\Delta x=2\pi mc(x_c-x_a)\)
so,
\(\bar F=2\pi mc\)
We know that,
\(F=-\psi\)
where \(F\) the Newtonian force due to \(\psi\). The average force on \(\psi\) is,
\(\bar F =-(-\bar \psi)=\bar\psi=2\pi mc\)
as the particle's \(\psi\) expanded from \(x_a\) to \(x_c\). Through out this process \(KE=\cfrac{1}{2}mc^2\) remains unchanged.
The average acceleration,
\(\bar a_c=2\pi c\)
Since the particle is in circular motion, and \(\bar F\) is along a radial line,
\(\bar F=2\pi c=\cfrac{c^2}{\bar x}\)
and
\(\bar x=\cfrac{c}{2\pi}\)
What is \(\bar x\)? \(\bar F\) is a hypothetical average force, that extends up to \(\bar x\) and is zero beyond. But be warned, all mathematical interpretations are fiction next to bullshit. Bullshit on the other hand, bulls will testify, is for real.
Have a nice day.
The Trouble With Being The Same Color
Reconciliation is easier with one common goal, but...
The particle is a standing wave along its circular path. Given \(x_c\), each \(x_d\) makes a unique angle \(\theta\). The spread of \(\theta\) depended on the range of \(x_d\) which in turn depends on the value of \(v^2_{min}\) from \(c^2\). (Post "A Pump!" dated 25 Jul 2015.) At \(v^2_{min}\) and \(x=x_{min}\) is the orbit of the particle at its lowest \(KE\), but at the furthest point on its oscillation path.
We have a wave of lowest \(KE\) around a circle of radius \(x_{min}\),
\(2\pi x_{min}=n\lambda_{min}\)
This wavelength, \(\lambda_{min}\) is likely to be the wavelength we associate color with. Valid values of \(x\) around \(x_{min}\) spread the color spectrum on both sides of \(x_{min}\). For each value of \(x\) there is a unique value for \(\theta\).
The particle is in a helical path of radius \(x_c\). The specific motion along \(\small{2\pi x_c}\) is changed, but \(x_d\) that indicates oscillation remains unchanged and the wavelength we associate color with is still \(\lambda_{min}\).
In both cases, they are still de Broglie standing wave of radius \(x_{min}\).
This explanation allows for two different material of different energies at the quantum level to have the same color. And it allows for the finite spectrum width of the emission from a laser, otherwise the emission spectrum from a laser associated with one energy level change is a very sharp line.
Note: \(2\pi x_c=n\lambda\) serve to illustrate de Broglie standing wave. The actual standing wave that we associate color with is at \(v^2_{min}\) with \(x=x_{min}\).
It does not matter whether the particle has a wave or a helical path around \(x_c\), for the discussion so far. The helical path gives the particle a spin.
The particle is a standing wave along its circular path. Given \(x_c\), each \(x_d\) makes a unique angle \(\theta\). The spread of \(\theta\) depended on the range of \(x_d\) which in turn depends on the value of \(v^2_{min}\) from \(c^2\). (Post "A Pump!" dated 25 Jul 2015.) At \(v^2_{min}\) and \(x=x_{min}\) is the orbit of the particle at its lowest \(KE\), but at the furthest point on its oscillation path.
We have a wave of lowest \(KE\) around a circle of radius \(x_{min}\),
\(2\pi x_{min}=n\lambda_{min}\)
This wavelength, \(\lambda_{min}\) is likely to be the wavelength we associate color with. Valid values of \(x\) around \(x_{min}\) spread the color spectrum on both sides of \(x_{min}\). For each value of \(x\) there is a unique value for \(\theta\).
The particle is in a helical path of radius \(x_c\). The specific motion along \(\small{2\pi x_c}\) is changed, but \(x_d\) that indicates oscillation remains unchanged and the wavelength we associate color with is still \(\lambda_{min}\).
In both cases, they are still de Broglie standing wave of radius \(x_{min}\).
This explanation allows for two different material of different energies at the quantum level to have the same color. And it allows for the finite spectrum width of the emission from a laser, otherwise the emission spectrum from a laser associated with one energy level change is a very sharp line.
Note: \(2\pi x_c=n\lambda\) serve to illustrate de Broglie standing wave. The actual standing wave that we associate color with is at \(v^2_{min}\) with \(x=x_{min}\).
It does not matter whether the particle has a wave or a helical path around \(x_c\), for the discussion so far. The helical path gives the particle a spin.
Birefringence Going Colorful
Cont'd from the post "In Colors", dated 11 Aug 2015,
Color dispersion is not birefringence, the spread of color is due to the spread of values of \(\theta\) in the light source that results in a spread of values in \(\Delta \theta\).
However, when the source is monochromatic, the ray will split as a result of \(\Delta\theta\). A single mono color dot will appear as two dots looking into the direction of refraction. This is birefringence. \(\Delta \theta\) is due to applying boundary conditions on \(B\) as in the post "A Bloom Crosses Over" dated 10 Aug 2015, where,
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(\varepsilon_1\), \(\varepsilon_2\) are electric permittivity.
Embedded charges in the material that changes \(\varepsilon\) will change \(\Delta \theta\) locally and possibly result in color patterns when illuminated with white light.
Birefringence and color dispersion may have the same underlying mechanism, but the factor leading to their manifestation is different. Color dispersion further requires a spread of \(\theta\).
\(B\) does not appear in the expressions for \(\alpha_{2s}\) and \(\alpha_{2p}\), as long as \(B\ne0\) both expressions are valid. Since in color dispersion, both \(\alpha_{2s}\) and \(\alpha_{2p}\) depended on color, \(B\) is not color.
The problem is, does turning a polarizer in white light let different color light through at different polarizing angle?
No, a polarizer is in fluorescence. Photons at different \(\theta\) are absorbed and emitted according to an emission distribution. This emission distribution has two dominant modes about \(\small{90^o}\) apart. (post "Not Exactly A Fluorescence Polarizer" dated 28 Jul 2015) . The color of the absorbed photons are destroyed. Colors are redistributed according to the emission distribution of the polarizer convoluted with the source color \(\theta\) distribution.
Unless photon absorption is selective based on \(\theta\), ie not a uniform distribution of \(\theta\) as assumed in the post "Not Exactly A Fluorescence Polarizer" dated 28 Jul 2015, then the emission distribution will be the convolution of the source distribution with the absorption distribution, and then the result convoluted with the emission distribution based on a uniformly distributed \(\theta\).
Colors are destroyed in a polarizer.
How then do we reconcile frequency/wavelength and \(\theta\)?
Tomorrow then...
Color dispersion is not birefringence, the spread of color is due to the spread of values of \(\theta\) in the light source that results in a spread of values in \(\Delta \theta\).
However, when the source is monochromatic, the ray will split as a result of \(\Delta\theta\). A single mono color dot will appear as two dots looking into the direction of refraction. This is birefringence. \(\Delta \theta\) is due to applying boundary conditions on \(B\) as in the post "A Bloom Crosses Over" dated 10 Aug 2015, where,
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(\varepsilon_1\), \(\varepsilon_2\) are electric permittivity.
Embedded charges in the material that changes \(\varepsilon\) will change \(\Delta \theta\) locally and possibly result in color patterns when illuminated with white light.
Birefringence and color dispersion may have the same underlying mechanism, but the factor leading to their manifestation is different. Color dispersion further requires a spread of \(\theta\).
\(B\) does not appear in the expressions for \(\alpha_{2s}\) and \(\alpha_{2p}\), as long as \(B\ne0\) both expressions are valid. Since in color dispersion, both \(\alpha_{2s}\) and \(\alpha_{2p}\) depended on color, \(B\) is not color.
The problem is, does turning a polarizer in white light let different color light through at different polarizing angle?
No, a polarizer is in fluorescence. Photons at different \(\theta\) are absorbed and emitted according to an emission distribution. This emission distribution has two dominant modes about \(\small{90^o}\) apart. (post "Not Exactly A Fluorescence Polarizer" dated 28 Jul 2015) . The color of the absorbed photons are destroyed. Colors are redistributed according to the emission distribution of the polarizer convoluted with the source color \(\theta\) distribution.
Unless photon absorption is selective based on \(\theta\), ie not a uniform distribution of \(\theta\) as assumed in the post "Not Exactly A Fluorescence Polarizer" dated 28 Jul 2015, then the emission distribution will be the convolution of the source distribution with the absorption distribution, and then the result convoluted with the emission distribution based on a uniformly distributed \(\theta\).
Colors are destroyed in a polarizer.
How then do we reconcile frequency/wavelength and \(\theta\)?
Tomorrow then...
Tuesday, August 11, 2015
In Colors
When \(\mu_2\gt\mu_1\) and \(\theta\) spread continuously over a range of vales,
Rays of different \(\theta\) spread between \(\alpha_2+\Delta\theta\) and \(\alpha_2-\Delta\theta\), equally on both sides of \(\alpha_2\).
From which we conclude color is \(\theta\) and white light has a spread of continuous \(\theta\). Two factors contribute to the spread: change in velocity on crossing into the medium and boundary conditions on \(B\) at the medium boundary.
These factors allows for different colored light to have the same velocity in the second medium and still be refracted to a different refraction angle resulting in the spread of colors. By Snell's Law alone different color lights have different refractive indices and have different velocities in the second medium in order to account for color dispersion.
Rays of different \(\theta\) spread between \(\alpha_2+\Delta\theta\) and \(\alpha_2-\Delta\theta\), equally on both sides of \(\alpha_2\).
From which we conclude color is \(\theta\) and white light has a spread of continuous \(\theta\). Two factors contribute to the spread: change in velocity on crossing into the medium and boundary conditions on \(B\) at the medium boundary.
These factors allows for different colored light to have the same velocity in the second medium and still be refracted to a different refraction angle resulting in the spread of colors. By Snell's Law alone different color lights have different refractive indices and have different velocities in the second medium in order to account for color dispersion.
They Did It Together
When we superimpose both the effects of change in speed along the direction of incidence, that gives us Snell's Law and boundary conditions applied to the \(B\) field at the medium interface, we have,
\(\alpha\to\alpha_2\)
For the case of \(\mu_2\gt\mu_1\),
\(\alpha_{2s}\lt\alpha_2+\Delta\theta\)
and
\(\alpha_{2p}\gt\alpha_2-\Delta\theta\)
For the case of \(\mu_2\lt\mu_1\),
\(\alpha_{2s}\gt\alpha_2+\Delta\theta\)
and
\(\alpha_{2p}\lt\alpha_2-\Delta\theta\)
When \(\Delta \theta=0\), the equations collapse to
\(\alpha_{2s}=\alpha_{2p}=\alpha_2\)
as we observe by Snell's Law for refraction alone. (We take the intersection of the two regions defining \(\alpha_{2s}\) and \(\alpha_{2p}\) after admitting the case of \(\mu_1=\mu_2\). )
It might appear that the split is due to the change in polarization \(\theta\) alone. In fact, both polarization, \(\theta\) and boundary conditions for the \(B\) field at the interface, contribute to refraction.
Note: \(\mu\ne n\)
\(\alpha\to\alpha_2\)
For the case of \(\mu_2\gt\mu_1\),
\(\alpha_{2s}\lt\alpha_2+\Delta\theta\)
and
\(\alpha_{2p}\gt\alpha_2-\Delta\theta\)
For the case of \(\mu_2\lt\mu_1\),
\(\alpha_{2s}\gt\alpha_2+\Delta\theta\)
and
\(\alpha_{2p}\lt\alpha_2-\Delta\theta\)
When \(\Delta \theta=0\), the equations collapse to
\(\alpha_{2s}=\alpha_{2p}=\alpha_2\)
as we observe by Snell's Law for refraction alone. (We take the intersection of the two regions defining \(\alpha_{2s}\) and \(\alpha_{2p}\) after admitting the case of \(\mu_1=\mu_2\). )
It might appear that the split is due to the change in polarization \(\theta\) alone. In fact, both polarization, \(\theta\) and boundary conditions for the \(B\) field at the interface, contribute to refraction.
Note: \(\mu\ne n\)
They Swing
Cont'd from "Left Side, Right Side, Bounded And Kinky" dated 10 Aug 2015,
For the case of \(\mu_2\gt\mu_1\),
\(\alpha_{2s}\lt\alpha+\Delta\theta\)
and
\(\alpha_{2p}\gt\alpha-\Delta\theta\)
It is possible that \(\alpha_{2s}\) crosses below \(\alpha_{2p}\) when \(\Delta\theta\lt0\). \(\alpha_{2s}\) is not necessarily the left beam. \(\Delta\theta\) can be adjusted to swing the beams over \(\alpha\).
For the case of \(\mu_2\gt\mu_1\),
\(\alpha_{2s}\lt\alpha+\Delta\theta\)
and
\(\alpha_{2p}\gt\alpha-\Delta\theta\)
It is possible that \(\alpha_{2s}\) crosses below \(\alpha_{2p}\) when \(\Delta\theta\lt0\). \(\alpha_{2s}\) is not necessarily the left beam. \(\Delta\theta\) can be adjusted to swing the beams over \(\alpha\).
Monday, August 10, 2015
Left Side, Right Side, Bounded And Kinky
Looking at the results from the post "Split Cannot Mend" dated 10 Aug 2015, what happen when,
\(\theta_2-\alpha_{2s}\lt0^o\)
and
\(\theta_2+\alpha_{2p}\gt90^o\) ??
And when \(\mu_2\gt\mu_1\)
\(\theta_2-\alpha_{2s}\gt\theta_1-\alpha\)
\(\alpha_{2s}\lt\theta_2-\theta_1+\alpha\)
and
\(\theta_2+\alpha_{2p}\gt\theta_1+\alpha\)
\(\alpha_{2p}\gt\alpha-(\theta_2-\theta_1)\)
If we define,
\(\Delta \theta=\theta_2-\theta_1\)
\(\alpha_{2s}\lt\alpha+\Delta\theta\)
and
\(\alpha_{2p}\gt\alpha-\Delta\theta\)
and the split occurs on the two sides about \(\alpha\) through the foot of the surface normal bounded by \(\pm\Delta \theta\)
When \(\mu_2\lt\mu_1\)
\(\theta_2-\alpha_{2s}\lt0^o\)
and
\(\theta_2+\alpha_{2p}\gt90^o\) ??
And when \(\mu_2\gt\mu_1\)
\(\theta_2-\alpha_{2s}\gt\theta_1-\alpha\)
\(\alpha_{2s}\lt\theta_2-\theta_1+\alpha\)
and
\(\theta_2+\alpha_{2p}\gt\theta_1+\alpha\)
\(\alpha_{2p}\gt\alpha-(\theta_2-\theta_1)\)
If we define,
\(\Delta \theta=\theta_2-\theta_1\)
\(\alpha_{2s}\lt\alpha+\Delta\theta\)
and
\(\alpha_{2p}\gt\alpha-\Delta\theta\)
and the split occurs on the two sides about \(\alpha\) through the foot of the surface normal bounded by \(\pm\Delta \theta\)
When \(\mu_2\lt\mu_1\)
\(\theta_2-\alpha_{2s}\lt\theta_1-\alpha\)
\(\alpha_{2s}\gt\alpha+\Delta \theta\)
and
\(\theta_2+\alpha_{2p}\lt\theta_1+\alpha\)
\(\alpha_{2p}\lt\alpha-\Delta \theta\)
Split Cannot Mend
Consider this,
\(\cfrac{\mu_2}{\mu_1}=\cfrac{tan(\theta_2-\alpha_{2s})}{tan(\theta_1-\alpha)}=\cfrac{tan(\theta_2+\alpha_{2p})}{tan(\theta_1+\alpha)}\)
\(tan(\theta_2-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha) \)
from which we may obtain \(\alpha_{2s}\). And
\(tan(\theta_2+\alpha_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha) \)
from which we may obtain \(\alpha_{2p}\).
And \(\theta_2\) is given by,
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
from the post "A Bloom Crosses Over" dated 10 Aug 2015.
The graph illustrates how to obtain \(\alpha_{2s}\) and \(\alpha_{2p}\).
\(\cfrac{\mu_2}{\mu_1}=\cfrac{tan(\theta_2-\alpha_{2s})}{tan(\theta_1-\alpha)}=\cfrac{tan(\theta_2+\alpha_{2p})}{tan(\theta_1+\alpha)}\)
\(tan(\theta_2-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha) \)
from which we may obtain \(\alpha_{2s}\). And
\(tan(\theta_2+\alpha_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha) \)
from which we may obtain \(\alpha_{2p}\).
And \(\theta_2\) is given by,
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
from the post "A Bloom Crosses Over" dated 10 Aug 2015.
The graph illustrates how to obtain \(\alpha_{2s}\) and \(\alpha_{2p}\).
Late Bloomer Gets The Splits
In the post "A Bloom Crosses Over" dated 10 Aug 2015, we have only considered the right edge of the cone. The left edge is refracted differently. Consider first, the left edge of the cone passing into the medium last,
since the base is perpendicular to the direction of incident, there is no need to adjust for \(\alpha\),
\(\cfrac { AB }{ v_{ 1 } } =\cfrac { A^{ ' }B^{ ' } }{ v_{ 2 } }\)
Since \(BA^{'}\) is common,
\(\cfrac {BA^{'} sin(\alpha _{1 }) }{ v_{ 1 } } =\cfrac {BA^{'} sin(\alpha _{ 2 }) }{ v_{ 2 } }\)
And
\(n.v=c\)
\(n\propto\cfrac{1}{v}\)
We have,
\(n_1sin(\alpha _{1 }) =n_2sin(\alpha _{ 2 }) \)
which is exactly Snell's Law. This is so, if the only factor resulting in refraction is the change in speed along the direction of incidence. We also have to consider how the \(B\) field behave at the interface.
When we consider the boundary conditions for the analogous \(B\) field on the right side of the cone, we have still,
\(B_1sin(\alpha_{adj\,\,1})=B_2sin(\alpha_{adj\,\,2})\)
\(\cfrac{B_1}{\mu_1}cos(\alpha_{adj\,\,1})=\cfrac{B_2}{\mu_2}cos(\alpha_{adj\,\,2})\)
\(\mu_1tan(\alpha _{adj\,\, 1 })=\mu_2tan(\alpha _{adj\,\, 2 })\)
where,
\(\alpha_{adj\,\,1}=90^o+\alpha_1-\theta_1\)
and
\(\alpha_{adj\,\,2}=90^o+\alpha_2-\theta_2\)
as such,
\(\mu_1cot(\theta_1-\alpha_1)=\mu_2cot(\theta_2-\alpha_2)\)
\(\cfrac{tan(\theta_2-\alpha_2)}{tan(\theta_1-\alpha_1)}=\cfrac{\mu_2}{\mu_1}\)
But on the left side of the cone,
\(\alpha_{adj}=\theta-(90^o-\alpha)=\theta+\alpha-90^o\)
\(B_1sin(\alpha_{adj\,\,1})=B_2sin(\alpha_{adj\,\,2})\)
\(\cfrac{B_1}{\mu_1}cos(\alpha_{adj\,\,1})=\cfrac{B_2}{\mu_2}cos(\alpha_{adj\,\,2})\)
Dividing these two expressions,
\(\mu_1tan(\alpha_{adj\,\,1})=\mu_2tan(\alpha_{adj\,\,2})\)
Substitute for \(\alpha_{adj}\),
\(\mu_1tan(\theta_1+\alpha_1-90^o)=\mu_2tan(\theta_2+\alpha_2-90^o)\)
\(\mu_1cot(\theta_1+\alpha_1)=\mu_2cot(\theta_2+\alpha_2)\)
\(\cfrac{tan(\theta_2+\alpha_2)}{tan(\theta_1+\alpha_1)}=\cfrac{\mu_2}{\mu_1}\)
When \(\theta\) is smaller such that,
\(\alpha_{adj}=(90^o-\alpha)-\theta=90^o-(\theta+\alpha)\)
we obtain the same expression,
\(\mu_1tan(90^o-(\theta_1+\alpha_1))=\mu_2tan(90^o-(\theta_2+\alpha_2))\)
\(\mu_1cot(\theta_1+\alpha_1)=\mu_2cot(\theta_2+\alpha_2)\)
\(\cfrac{tan(\theta_2+\alpha_2)}{tan(\theta_1+\alpha_1)}=\cfrac{\mu_2}{\mu_1}\)
This means the ray will split into two, depending on which side of the cone the particle is on when it passes into the medium.
Banana!
since the base is perpendicular to the direction of incident, there is no need to adjust for \(\alpha\),
\(\cfrac { AB }{ v_{ 1 } } =\cfrac { A^{ ' }B^{ ' } }{ v_{ 2 } }\)
Since \(BA^{'}\) is common,
\(\cfrac {BA^{'} sin(\alpha _{1 }) }{ v_{ 1 } } =\cfrac {BA^{'} sin(\alpha _{ 2 }) }{ v_{ 2 } }\)
And
\(n.v=c\)
\(n\propto\cfrac{1}{v}\)
We have,
\(n_1sin(\alpha _{1 }) =n_2sin(\alpha _{ 2 }) \)
which is exactly Snell's Law. This is so, if the only factor resulting in refraction is the change in speed along the direction of incidence. We also have to consider how the \(B\) field behave at the interface.
When we consider the boundary conditions for the analogous \(B\) field on the right side of the cone, we have still,
\(B_1sin(\alpha_{adj\,\,1})=B_2sin(\alpha_{adj\,\,2})\)
\(\cfrac{B_1}{\mu_1}cos(\alpha_{adj\,\,1})=\cfrac{B_2}{\mu_2}cos(\alpha_{adj\,\,2})\)
\(\mu_1tan(\alpha _{adj\,\, 1 })=\mu_2tan(\alpha _{adj\,\, 2 })\)
where,
\(\alpha_{adj\,\,1}=90^o+\alpha_1-\theta_1\)
and
\(\alpha_{adj\,\,2}=90^o+\alpha_2-\theta_2\)
as such,
\(\mu_1cot(\theta_1-\alpha_1)=\mu_2cot(\theta_2-\alpha_2)\)
\(\cfrac{tan(\theta_2-\alpha_2)}{tan(\theta_1-\alpha_1)}=\cfrac{\mu_2}{\mu_1}\)
But on the left side of the cone,
\(\alpha_{adj}=\theta-(90^o-\alpha)=\theta+\alpha-90^o\)
\(B_1sin(\alpha_{adj\,\,1})=B_2sin(\alpha_{adj\,\,2})\)
\(\cfrac{B_1}{\mu_1}cos(\alpha_{adj\,\,1})=\cfrac{B_2}{\mu_2}cos(\alpha_{adj\,\,2})\)
Dividing these two expressions,
\(\mu_1tan(\alpha_{adj\,\,1})=\mu_2tan(\alpha_{adj\,\,2})\)
Substitute for \(\alpha_{adj}\),
\(\mu_1tan(\theta_1+\alpha_1-90^o)=\mu_2tan(\theta_2+\alpha_2-90^o)\)
\(\mu_1cot(\theta_1+\alpha_1)=\mu_2cot(\theta_2+\alpha_2)\)
When \(\theta\) is smaller such that,
\(\alpha_{adj}=(90^o-\alpha)-\theta=90^o-(\theta+\alpha)\)
we obtain the same expression,
\(\mu_1tan(90^o-(\theta_1+\alpha_1))=\mu_2tan(90^o-(\theta_2+\alpha_2))\)
\(\mu_1cot(\theta_1+\alpha_1)=\mu_2cot(\theta_2+\alpha_2)\)
\(\cfrac{tan(\theta_2+\alpha_2)}{tan(\theta_1+\alpha_1)}=\cfrac{\mu_2}{\mu_1}\)
This means the ray will split into two, depending on which side of the cone the particle is on when it passes into the medium.
Banana!
A Bloom Crosses Over
When a photon, modeled as a cone shaped spread of \(E\) field, is projected perpendicular from a medium of refractive index \(n_1\) into a medium of refractive index \(n_2\),
The \(E\) field being resolved into three components as shown, and applying the boundary conditions for an \(E\) field line,
\(E_{1\,3}=\cfrac{\varepsilon_2}{\varepsilon_1}E_{2\,3}\)
where the subscript \(3\) denotes the perpendicular direction, parallel to the surface normal.
\(E_{1}cos(\beta_1)=\cfrac{\varepsilon_2}{\varepsilon_1}E_{2}cos(\beta_2)\)
The tangential component remains the same,
\(E_1 sin(\beta_1)=E_2sin(\beta_2)\)
Dividing the two expressions above, we have,
\(\cfrac{ tan(\beta_2)}{tan(\beta_1)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
Since, \(\beta=90^o-\theta\)
\(tan(\beta)=tan(90^o-\theta)=cot(\theta)\)
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
When the dielectric constants,
\(\varepsilon_1\lt\varepsilon_2\)
The \(E\) field cone spreads and polarization \(\small{\theta}\) decreases. This is however, not dispersion.
When the photon is projected at an incline to the normal onto the interface \(\small{\varepsilon_1|\varepsilon_2}\),
The particle maintains its circular motion in both medium and the cone passes through the medium completely when its apex is on the interface, at the foot of the surface normal, we have,
\(\cfrac { AB }{ v_{ 1 } } =\cfrac { A^{ ' }B^{ ' } }{ v_{ 2 } } \)
Since \(BA^{'}\) is common,
\( \cfrac {BA^{'} sin(\alpha _{adj\,\, 1 }) }{ v_{ 1 } } =\cfrac {BA^{'} sin(\alpha _{adj\,\, 2 }) }{ v_{ 2 } } \)
where,
\(\alpha_{adj\,\,1}=90^o+\alpha_1-\theta_1\)
and
\(\alpha_{adj\,\,2}=90^o+\alpha_2-\theta_2\)
where \(\theta\) is polarization; the angle at which the circular path of the particle makes with the line of incidence.
Since,
\( n.v=c\)
\(\cfrac{1}{v}\propto n\)
and we have,
\( n_{ 1 }sin(\alpha _{adj\,\, 1 })=n_{ 2 }sin(\alpha _{ adj\,\,2 })\)
which is just Snell's Law with \(\alpha\) substituted by \(\alpha_{adj}\). Furthermore, this particle in circular motion that generates a \(E\) field is itself a \(B\) field. When we apply the boundary conditions appropriate for a \(B\) field upon the circulating particle at the point through the incident normal,
the normal components of \(B\) across the mediums are equal,
\(B_{ 1 }sin(\alpha _{ adj\,\,1 })=B_{ 2 }sin(\alpha _{ adj\,\,2 })\)
where,
\(\alpha_{adj\,\,1}=90^o+\alpha_1-\theta_1\)
and
\(\alpha_{adj\,\,2}=90^o+\alpha_2-\theta_2\)
where \(\theta\) is polarization; the angle at which the circular path of the particle makes with the line of incidence.
\( \cfrac { B_{ 1 } }{ B_{ 2 } } =\cfrac { sin(\alpha _{ adj\,\,2 }) }{ sin(\alpha _{ adj\,\,1 }) } \)
and the tangential component of \(H=\cfrac{B}{\mu}\) across the medium are equal,
\(\cfrac { B_{ 1 }cos(\alpha _{adj\,\, 1 }) }{ \mu _{ 1 } } =\cfrac { B_{ 2 }cos(\alpha _{adj\,\, 2 }) }{ \mu _{ 2 } } \)
So,
\( \cfrac { sin(\alpha _{ adj\,\,2 }) }{ sin(\alpha _{ adj\,\,1 }) } =\cfrac { \mu _{ 1 } }{ \mu _{ 2 } } \cfrac { cos(\alpha _{ adj\,\,2 }) }{ cos(\alpha _{ adj\,\,1 }) } \)
\( \cfrac { tan(\alpha _{ adj\,\,2 }) }{ tan(\alpha _{adj\,\, 1 }) } =\cfrac { \mu _{ 1 } }{ \mu _{ 2 } } \)
\(\mu_1tan(\alpha _{adj\,\, 1 })=\mu_2tan(\alpha _{adj\,\, 2 })\) ---(*)
Snell's law is due to the change in velocity along the ray with the particle still in circular motion in the perpendicular direction, at \(AA^{'}\) and \(BB^{'}\). The last expression (*) is the result of applying boundary conditions on the analogous \(B\) field. Applying boundary conditions to the \(E\) field indicates a change in polarization \(\theta\) as the photon crosses the interface \(\small{\varepsilon_1|\varepsilon_2}\).
In the case of an EMW, the \(E\) field is reversed, but all expressions developed above are still true.
The \(E\) field being resolved into three components as shown, and applying the boundary conditions for an \(E\) field line,
\(E_{1\,3}=\cfrac{\varepsilon_2}{\varepsilon_1}E_{2\,3}\)
where the subscript \(3\) denotes the perpendicular direction, parallel to the surface normal.
\(E_{1}cos(\beta_1)=\cfrac{\varepsilon_2}{\varepsilon_1}E_{2}cos(\beta_2)\)
The tangential component remains the same,
\(E_1 sin(\beta_1)=E_2sin(\beta_2)\)
Dividing the two expressions above, we have,
\(\cfrac{ tan(\beta_2)}{tan(\beta_1)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
Since, \(\beta=90^o-\theta\)
\(tan(\beta)=tan(90^o-\theta)=cot(\theta)\)
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
When the dielectric constants,
\(\varepsilon_1\lt\varepsilon_2\)
The \(E\) field cone spreads and polarization \(\small{\theta}\) decreases. This is however, not dispersion.
When the photon is projected at an incline to the normal onto the interface \(\small{\varepsilon_1|\varepsilon_2}\),
The particle maintains its circular motion in both medium and the cone passes through the medium completely when its apex is on the interface, at the foot of the surface normal, we have,
\(\cfrac { AB }{ v_{ 1 } } =\cfrac { A^{ ' }B^{ ' } }{ v_{ 2 } } \)
Since \(BA^{'}\) is common,
\( \cfrac {BA^{'} sin(\alpha _{adj\,\, 1 }) }{ v_{ 1 } } =\cfrac {BA^{'} sin(\alpha _{adj\,\, 2 }) }{ v_{ 2 } } \)
where,
\(\alpha_{adj\,\,1}=90^o+\alpha_1-\theta_1\)
and
\(\alpha_{adj\,\,2}=90^o+\alpha_2-\theta_2\)
where \(\theta\) is polarization; the angle at which the circular path of the particle makes with the line of incidence.
Since,
\( n.v=c\)
\(\cfrac{1}{v}\propto n\)
and we have,
\( n_{ 1 }sin(\alpha _{adj\,\, 1 })=n_{ 2 }sin(\alpha _{ adj\,\,2 })\)
which is just Snell's Law with \(\alpha\) substituted by \(\alpha_{adj}\). Furthermore, this particle in circular motion that generates a \(E\) field is itself a \(B\) field. When we apply the boundary conditions appropriate for a \(B\) field upon the circulating particle at the point through the incident normal,
the normal components of \(B\) across the mediums are equal,
\(B_{ 1 }sin(\alpha _{ adj\,\,1 })=B_{ 2 }sin(\alpha _{ adj\,\,2 })\)
where,
\(\alpha_{adj\,\,1}=90^o+\alpha_1-\theta_1\)
and
\(\alpha_{adj\,\,2}=90^o+\alpha_2-\theta_2\)
where \(\theta\) is polarization; the angle at which the circular path of the particle makes with the line of incidence.
\( \cfrac { B_{ 1 } }{ B_{ 2 } } =\cfrac { sin(\alpha _{ adj\,\,2 }) }{ sin(\alpha _{ adj\,\,1 }) } \)
and the tangential component of \(H=\cfrac{B}{\mu}\) across the medium are equal,
\(\cfrac { B_{ 1 }cos(\alpha _{adj\,\, 1 }) }{ \mu _{ 1 } } =\cfrac { B_{ 2 }cos(\alpha _{adj\,\, 2 }) }{ \mu _{ 2 } } \)
So,
\( \cfrac { sin(\alpha _{ adj\,\,2 }) }{ sin(\alpha _{ adj\,\,1 }) } =\cfrac { \mu _{ 1 } }{ \mu _{ 2 } } \cfrac { cos(\alpha _{ adj\,\,2 }) }{ cos(\alpha _{ adj\,\,1 }) } \)
\( \cfrac { tan(\alpha _{ adj\,\,2 }) }{ tan(\alpha _{adj\,\, 1 }) } =\cfrac { \mu _{ 1 } }{ \mu _{ 2 } } \)
\(\mu_1tan(\alpha _{adj\,\, 1 })=\mu_2tan(\alpha _{adj\,\, 2 })\) ---(*)
Snell's law is due to the change in velocity along the ray with the particle still in circular motion in the perpendicular direction, at \(AA^{'}\) and \(BB^{'}\). The last expression (*) is the result of applying boundary conditions on the analogous \(B\) field. Applying boundary conditions to the \(E\) field indicates a change in polarization \(\theta\) as the photon crosses the interface \(\small{\varepsilon_1|\varepsilon_2}\).
In the case of an EMW, the \(E\) field is reversed, but all expressions developed above are still true.
Sunday, August 9, 2015
Dispersion of EMW And Photons
In both EMW and photon, dispersion results from \(\small{\theta\lt90^o}\), due to the non zero vertical component of \(E\).
When \(\small{\theta=90^o}\) there is no dispersion.
When \(\small{\theta=90^o}\) there is no dispersion.
Counter Force Components?
Continued from the previous post "Cosmetics Attracting Attentions" dated 08 Aug 2015,
Still, the physical significance of these angles are not obvious on paper.
Is this in total,
\(\cfrac{3\pi}{4}+\cfrac{\pi}{4}=\pi\)
a \(\small{180^o}\) phase difference between \(F_\rho\) and \(x\) when \(F_\rho\) is sinusoidal.
Still, the physical significance of these angles are not obvious on paper.
Is this in total,
\(\cfrac{3\pi}{4}+\cfrac{\pi}{4}=\pi\)
a \(\small{180^o}\) phase difference between \(F_\rho\) and \(x\) when \(F_\rho\) is sinusoidal.
Cosmetics Attracting Attentions
From the post ""the post "Not Exponential, But Hyperbolic And Positive Gravity!" dated 22 Nov 2014,
\(F_{\rho}=e^{ i3\pi /4 }D\sqrt { 2{ mc^{ 2 } } } .tanh\left( \cfrac { { D } }{ \sqrt { 2{ mc^{ 2 } } } }( x-x_o).e^{ i\pi /4 } \right)\)
where we insist that,
\(G=D.e^{ i\pi /4 }\)
is real,
But given,
\(tanh(x)=\cfrac{e^x-e^{-x}}{e^x+e^{-x}}=\cfrac{1-e^{-2x}}{1+e^{-2x}}\)
D can be real.
Consider,
\(e^{ i\pi /4 }=(e^{ i\pi /2 })^{1/2}=\sqrt{i}\)
that follows from Euler's
\(e^{i\pi}+1=0\)
An so,
\(tanh(h\sqrt{i})=\cfrac{1-e^{-2h\sqrt{i}}}{1+e^{-2h\sqrt{i}}}\)
where
\(h=\cfrac { { D } }{ \sqrt { 2{ mc^{ 2 } } } }( x-x_o)\)
and
\(e^{ i3\pi /4 }=i^{3/2}=i\sqrt{i}\)
\(F_{\rho}=i\sqrt{i}.D\sqrt { 2{ mc^{ 2 } } } .\cfrac{1-e^{-2h\sqrt{i}}}{1+e^{-2h\sqrt{i}}}\)
and if we define,
\(\varphi=\sqrt{i}\)
\(F_{\rho}=\varphi^3.D\sqrt { 2{ mc^{ 2 } } } .\cfrac{1-e^{-2\varphi h}}{1+e^{-2\varphi h}}\)
where
\(\varphi\) rotates \(45^o\) and \(\varphi^3\) rotates \(135^o\) from the direction of \(x\).
Cosmetics to bring attention to the these two rotations; they have significance, but what?
Furthermore,
\(\sqrt{2mc^2}=\sqrt{m(\sqrt{2}c)^2}\)
also has significance; it implies that across two orthogonal dimensions, in place of \(c\) is \(\sqrt{2}c\). This suggests that if entanglement is the reason for light speed limit, then entanglement is dimension specific, a different type of entanglement occurs along each orthogonal dimension; a different entanglement of the specific energy defining that dimension. Particles can be limited separately along \(t_c\) where in entanglement with other particles share electrostatic energy, and at the same time limited along \(t_g\) where they share gravitational energy; ditto for \(t_T\).
Since we normally dealt with energy of a particular sort, \(\sqrt{2}c\) has never arise until we cross between orthogonal dimensions.
In space,
\(c^2+c^2=2c^2\)
\(2c^2+c^2=3c^2\)
And the speed limit we encountered first was,
\(c=\sqrt{3}k\)
where \(k\) is a constant, \(c\) light speed. Three groups of particles entangled separately across three space dimensions with the one particle under observation.
Note: \(\small{\sqrt{3}=1.7320508075688773...}\) is not rational. Looking for more significant numbers to \(c\) may just be chasing after the tail of \(\small{\sqrt{3}}\).
\(F_{\rho}=e^{ i3\pi /4 }D\sqrt { 2{ mc^{ 2 } } } .tanh\left( \cfrac { { D } }{ \sqrt { 2{ mc^{ 2 } } } }( x-x_o).e^{ i\pi /4 } \right)\)
where we insist that,
\(G=D.e^{ i\pi /4 }\)
is real,
But given,
\(tanh(x)=\cfrac{e^x-e^{-x}}{e^x+e^{-x}}=\cfrac{1-e^{-2x}}{1+e^{-2x}}\)
D can be real.
Consider,
\(e^{ i\pi /4 }=(e^{ i\pi /2 })^{1/2}=\sqrt{i}\)
that follows from Euler's
\(e^{i\pi}+1=0\)
An so,
\(tanh(h\sqrt{i})=\cfrac{1-e^{-2h\sqrt{i}}}{1+e^{-2h\sqrt{i}}}\)
where
\(h=\cfrac { { D } }{ \sqrt { 2{ mc^{ 2 } } } }( x-x_o)\)
and
\(e^{ i3\pi /4 }=i^{3/2}=i\sqrt{i}\)
\(F_{\rho}=i\sqrt{i}.D\sqrt { 2{ mc^{ 2 } } } .\cfrac{1-e^{-2h\sqrt{i}}}{1+e^{-2h\sqrt{i}}}\)
and if we define,
\(\varphi=\sqrt{i}\)
\(F_{\rho}=\varphi^3.D\sqrt { 2{ mc^{ 2 } } } .\cfrac{1-e^{-2\varphi h}}{1+e^{-2\varphi h}}\)
where
\(\varphi\) rotates \(45^o\) and \(\varphi^3\) rotates \(135^o\) from the direction of \(x\).
Cosmetics to bring attention to the these two rotations; they have significance, but what?
Furthermore,
\(\sqrt{2mc^2}=\sqrt{m(\sqrt{2}c)^2}\)
also has significance; it implies that across two orthogonal dimensions, in place of \(c\) is \(\sqrt{2}c\). This suggests that if entanglement is the reason for light speed limit, then entanglement is dimension specific, a different type of entanglement occurs along each orthogonal dimension; a different entanglement of the specific energy defining that dimension. Particles can be limited separately along \(t_c\) where in entanglement with other particles share electrostatic energy, and at the same time limited along \(t_g\) where they share gravitational energy; ditto for \(t_T\).
Since we normally dealt with energy of a particular sort, \(\sqrt{2}c\) has never arise until we cross between orthogonal dimensions.
In space,
\(c^2+c^2=2c^2\)
\(2c^2+c^2=3c^2\)
And the speed limit we encountered first was,
\(c=\sqrt{3}k\)
where \(k\) is a constant, \(c\) light speed. Three groups of particles entangled separately across three space dimensions with the one particle under observation.
Note: \(\small{\sqrt{3}=1.7320508075688773...}\) is not rational. Looking for more significant numbers to \(c\) may just be chasing after the tail of \(\small{\sqrt{3}}\).