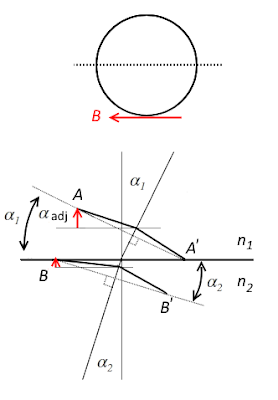
since the base is perpendicular to the direction of incident, there is no need to adjust for \(\alpha\),
\(\cfrac { AB }{ v_{ 1 } } =\cfrac { A^{ ' }B^{ ' } }{ v_{ 2 } }\)
Since \(BA^{'}\) is common,
\(\cfrac {BA^{'} sin(\alpha _{1 }) }{ v_{ 1 } } =\cfrac {BA^{'} sin(\alpha _{ 2 }) }{ v_{ 2 } }\)
And
\(n.v=c\)
\(n\propto\cfrac{1}{v}\)
We have,
\(n_1sin(\alpha _{1 }) =n_2sin(\alpha _{ 2 }) \)
which is exactly Snell's Law. This is so, if the only factor resulting in refraction is the change in speed along the direction of incidence. We also have to consider how the \(B\) field behave at the interface.
When we consider the boundary conditions for the analogous \(B\) field on the right side of the cone, we have still,
\(B_1sin(\alpha_{adj\,\,1})=B_2sin(\alpha_{adj\,\,2})\)
\(\cfrac{B_1}{\mu_1}cos(\alpha_{adj\,\,1})=\cfrac{B_2}{\mu_2}cos(\alpha_{adj\,\,2})\)
\(\mu_1tan(\alpha _{adj\,\, 1 })=\mu_2tan(\alpha _{adj\,\, 2 })\)
where,
\(\alpha_{adj\,\,1}=90^o+\alpha_1-\theta_1\)
and
\(\alpha_{adj\,\,2}=90^o+\alpha_2-\theta_2\)
as such,
\(\mu_1cot(\theta_1-\alpha_1)=\mu_2cot(\theta_2-\alpha_2)\)
\(\cfrac{tan(\theta_2-\alpha_2)}{tan(\theta_1-\alpha_1)}=\cfrac{\mu_2}{\mu_1}\)
But on the left side of the cone,
\(\alpha_{adj}=\theta-(90^o-\alpha)=\theta+\alpha-90^o\)
\(B_1sin(\alpha_{adj\,\,1})=B_2sin(\alpha_{adj\,\,2})\)
\(\cfrac{B_1}{\mu_1}cos(\alpha_{adj\,\,1})=\cfrac{B_2}{\mu_2}cos(\alpha_{adj\,\,2})\)
Dividing these two expressions,
\(\mu_1tan(\alpha_{adj\,\,1})=\mu_2tan(\alpha_{adj\,\,2})\)
Substitute for \(\alpha_{adj}\),
\(\mu_1tan(\theta_1+\alpha_1-90^o)=\mu_2tan(\theta_2+\alpha_2-90^o)\)
\(\mu_1cot(\theta_1+\alpha_1)=\mu_2cot(\theta_2+\alpha_2)\)
When \(\theta\) is smaller such that,
\(\alpha_{adj}=(90^o-\alpha)-\theta=90^o-(\theta+\alpha)\)
we obtain the same expression,
\(\mu_1tan(90^o-(\theta_1+\alpha_1))=\mu_2tan(90^o-(\theta_2+\alpha_2))\)
\(\mu_1cot(\theta_1+\alpha_1)=\mu_2cot(\theta_2+\alpha_2)\)
\(\cfrac{tan(\theta_2+\alpha_2)}{tan(\theta_1+\alpha_1)}=\cfrac{\mu_2}{\mu_1}\)
This means the ray will split into two, depending on which side of the cone the particle is on when it passes into the medium.
Banana!