If water is magnetic, how does it work? Water being magnetic will help explain the formation of water droplets, but that would be jumping the gun.
What else is in optics? Plenty!
In the case of Lambert's cosine law, where intensity is directly proportional to the incident angle, but as noted in the post "No \(B\), Speed Alone" dated 25 Aug 2015, since the two loops makes an angle \(\theta\) with the ray,
\(cos(\alpha)\to cos(\alpha_{adj})=cos(\alpha+90^o-\theta)=-sin(\alpha-\theta)=sin(\theta-\alpha)\)
and
\(cos(\alpha)\to cos(\alpha_{adj})=cos(\alpha-90^o+\theta)=sin(\alpha+\theta)\)
as we adjust for the angle of incident between the loops and the surface normal at the point of reflection, we have an adjusted Lambert, where the intensity of an ideal diffusely reflecting surface is proportional to,
\(sin(\theta-\alpha)+sin(\theta+\alpha)=sin(\theta)cos(\alpha)\)
\(\alpha\) is the incident angle of the ray, and \(\theta\) is the angle the loops make with the ray, polarization.
Since \(\theta\) is distributed over a range of values, \(0\lt\theta\lt\pi/2\), intensity \(I\),
\(I\propto\int^{\pi/2}_0{f(\theta)sin(\theta)}d\theta.cos(\alpha)\)
where
\(f(\theta)=\cfrac{2\theta}{\pi(1+\theta^4)}\)
from the post "Not Exactly A Fluorescence Polarizer" dated 28 Jul 2015. The problem is with the abrupt cutoff at \(\pi/2\), may be
\(I\propto\int^{\theta\to\infty}_0{f(\theta)sin(\theta)}d\theta.cos(\alpha)\)
or even,
\(I\propto\int^{\theta\to\infty}_{\theta\to -\infty}{f(\theta)sin(\theta)}d\theta.cos(\alpha)\)
Only after \(\theta\) has been accounted for, (for example, \(\theta=90^o\)) is it possible to have a constant \(A\) such that,
\(I=AF(\theta).cos(\alpha)\)
where \(F(\theta)\) is a function of \(\theta\) only. In the case \(\theta=90^o\), a laser source,
\(I=A.cos(\alpha)\)
where \(A\) is a constant.
Wednesday, August 26, 2015
Tuesday, August 25, 2015
No \(B\), Speed Alone
Why does total internal reflection occur?
From the post "Wave Front and Wave Back" dated 18 May 2014, a photon was conceptualized as a particle in helical motion,
\(\cfrac{x_{v1}}{cos(\alpha_1)}=\cfrac{x_{v2}}{cos(\alpha_2)}\)
\(x_{v2}=x_{v1}\cfrac{cos(\alpha_2)}{cos(\alpha_1)}\)
where \(x_{v1}\), \(x_{v2}\) are the radii of circular motion in medium 1 and 2 respectively.
and
\(\cfrac{\lambda}{n_1sin(\alpha_1)}=\cfrac{\lambda}{n_2sin(\alpha_2)}\)
\(sin(\alpha_2)=\cfrac{n_1}{n_2}sin(\alpha_1)\)
So,
\(x_{v2}=\cfrac{x_{v1}}{cos(\alpha_1)}\sqrt{1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)}\)
when the particle enters into to less dense medium,
\(n_2\lt n_1\)
\(1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)\lt 0\)
in which case, \(x_{v2}\) is complex and is rotated by \(90^o\) clockwise at the point of ncident,
\(x_{v2}=i.\cfrac{x_{v1}}{cos(\alpha_1)}\sqrt{\left|1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)\right|}\)
and \(\alpha_2\) is totally internally reflected. When
\(1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)=0\)
\(sin(\alpha_1)=sin(\alpha_c)=\cfrac{n_2}{n_1}\)
where \(\alpha_c\) is the critical angle. Unfortunately, the formula is valid only up to \(\alpha_c\). For incident angle greater than \(\alpha_c\), we know that the ray is reflected,
\(x_{v2}={x_{v1}}\)
\(1=\cfrac{cos(\alpha_2)}{cos(\alpha_1)}\)
\(\alpha_1=\alpha_2\)
both angles measured from the normal on medium \(n_1\).
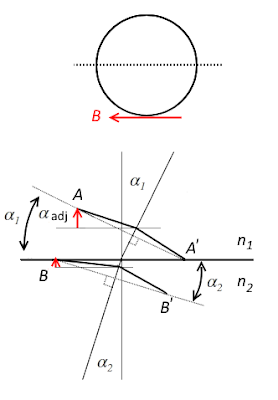
This derivation for total internal reflection considers the relative speeds of the particle in the two mediums alone; \(B\) fields are not involved. Since, both loops are perpendicular to the ray \(\alpha\) only in the limiting case of \(\theta\to90^o\), the following adjustments are necessary to the values of \(\alpha\) for each of the loop as illustrated,
\(\alpha_{adj}=\alpha+90^o-\theta\)
and
\(\alpha_{adj}=\alpha-90^o+\theta\)
which indicate that the two loops can be separated (circular polarization\(\to\)linear polarization) when,
since \(\alpha\lt90^o\)
\(\alpha-90^o+\theta\lt\alpha_c\)
\(\alpha\lt\alpha_c+90^o-\theta\)
and
\(\alpha+90^o-\theta\gt\alpha_c\)
\(\alpha\gt\alpha_c-90^o+\theta\)
where \(\alpha_{2}^{'}\) has been totally internally reflected. When \(\theta\to90^o\), the range of \(\alpha\) collapses to a single value \(\alpha_c\), as \(\alpha_{adj}\to\alpha\).
From the post "Wave Front and Wave Back" dated 18 May 2014, a photon was conceptualized as a particle in helical motion,
\(\cfrac{x_{v1}}{cos(\alpha_1)}=\cfrac{x_{v2}}{cos(\alpha_2)}\)
\(x_{v2}=x_{v1}\cfrac{cos(\alpha_2)}{cos(\alpha_1)}\)
where \(x_{v1}\), \(x_{v2}\) are the radii of circular motion in medium 1 and 2 respectively.
and
\(\cfrac{\lambda}{n_1sin(\alpha_1)}=\cfrac{\lambda}{n_2sin(\alpha_2)}\)
\(sin(\alpha_2)=\cfrac{n_1}{n_2}sin(\alpha_1)\)
So,
\(x_{v2}=\cfrac{x_{v1}}{cos(\alpha_1)}\sqrt{1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)}\)
when the particle enters into to less dense medium,
\(n_2\lt n_1\)
\(1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)\lt 0\)
in which case, \(x_{v2}\) is complex and is rotated by \(90^o\) clockwise at the point of ncident,
\(x_{v2}=i.\cfrac{x_{v1}}{cos(\alpha_1)}\sqrt{\left|1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)\right|}\)
and \(\alpha_2\) is totally internally reflected. When
\(1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)=0\)
\(sin(\alpha_1)=sin(\alpha_c)=\cfrac{n_2}{n_1}\)
where \(\alpha_c\) is the critical angle. Unfortunately, the formula is valid only up to \(\alpha_c\). For incident angle greater than \(\alpha_c\), we know that the ray is reflected,
\(x_{v2}={x_{v1}}\)
\(1=\cfrac{cos(\alpha_2)}{cos(\alpha_1)}\)
\(\alpha_1=\alpha_2\)
both angles measured from the normal on medium \(n_1\).
This derivation for total internal reflection considers the relative speeds of the particle in the two mediums alone; \(B\) fields are not involved. Since, both loops are perpendicular to the ray \(\alpha\) only in the limiting case of \(\theta\to90^o\), the following adjustments are necessary to the values of \(\alpha\) for each of the loop as illustrated,
\(\alpha_{adj}=\alpha+90^o-\theta\)
and
\(\alpha_{adj}=\alpha-90^o+\theta\)
which indicate that the two loops can be separated (circular polarization\(\to\)linear polarization) when,
since \(\alpha\lt90^o\)
\(\alpha-90^o+\theta\lt\alpha_c\)
\(\alpha\lt\alpha_c+90^o-\theta\)
and
\(\alpha+90^o-\theta\gt\alpha_c\)
\(\alpha\gt\alpha_c-90^o+\theta\)
where \(\alpha_{2}^{'}\) has been totally internally reflected. When \(\theta\to90^o\), the range of \(\alpha\) collapses to a single value \(\alpha_c\), as \(\alpha_{adj}\to\alpha\).
Fractured Science
What happens when \(\theta=90^o-\alpha\)?
In this case, the loop parallel to the interface passes through the medium unrefracted (there is no refraction due to the boundary conditions on \(B\), but the ray is still refracted due to a change in velocity of the ray). The other loop is reflected and the center line of this ray intersects the interface behind the point of reflection and
\(d\lt0\)
\(d\), the lateral shift is negative.
When \(\theta=\alpha\),
One loop passes perpendicularly into the less dense medium at the point of reflection and is refracted in the less dense medium as the result of an increase in velocity. The other is reflected when the incident angle \(\alpha\gt\) critical angle.
Notice that as the right loop enters into the less dense medium, the particle has a parallel velocity component that is opposite to the parallel velocity component of the ray. The particle is travelling in the reverse direction to the ray, along the interface. And the adjusted angle that the loop makes with the normal is,
\(\alpha_{adj}=-\left( 90^{ o }-\alpha -\theta \right) \)
this suggest that the ray is refracted back into the same side of the normal as the incident ray,
which would be very odd indeed.
This approach is flawed as the underlying mechanism of total internal reflection possibly as the result of applying boundary conditions on the ray's \(B\) field has not been explored yet. Previously, there is a change in direction in the ray, as its normal and parallel \(B\) field components are effected differently at the boundary.
Note: If, however changes in speed alone can provide for total internal reflection (post "No \(B\), Speed Alone" dated 25 Aug 2015), then the above can be superimposed onto the results for total internal reflection as before.
In this case, the loop parallel to the interface passes through the medium unrefracted (there is no refraction due to the boundary conditions on \(B\), but the ray is still refracted due to a change in velocity of the ray). The other loop is reflected and the center line of this ray intersects the interface behind the point of reflection and
\(d\lt0\)
\(d\), the lateral shift is negative.
When \(\theta=\alpha\),
One loop passes perpendicularly into the less dense medium at the point of reflection and is refracted in the less dense medium as the result of an increase in velocity. The other is reflected when the incident angle \(\alpha\gt\) critical angle.
Notice that as the right loop enters into the less dense medium, the particle has a parallel velocity component that is opposite to the parallel velocity component of the ray. The particle is travelling in the reverse direction to the ray, along the interface. And the adjusted angle that the loop makes with the normal is,
\(\alpha_{adj}=-\left( 90^{ o }-\alpha -\theta \right) \)
this suggest that the ray is refracted back into the same side of the normal as the incident ray,
which would be very odd indeed.
This approach is flawed as the underlying mechanism of total internal reflection possibly as the result of applying boundary conditions on the ray's \(B\) field has not been explored yet. Previously, there is a change in direction in the ray, as its normal and parallel \(B\) field components are effected differently at the boundary.
Note: If, however changes in speed alone can provide for total internal reflection (post "No \(B\), Speed Alone" dated 25 Aug 2015), then the above can be superimposed onto the results for total internal reflection as before.
Yet Another Time Singularity
Goos–Hänchen effect? Where \(n_2\lt n_1\),
The particle on the lower loop and the upper loop, where the last point to enter into the second medium is the earliest and the latest respectively, are reflected at different points along the interface. The ray splits into two beams. In order to be reflected, this last point is lifted off the interface just as it enters into the second medium. The distance between the two point of reflection,
\(d=2x_vsin(\theta).\cfrac{1}{sin(90^o-\alpha)}\)
where \(x_v\) is the radius of circular motion of the particle displace from the \(\psi\) cloud center. The separation between the two rays is,
\(d_b=d.{sin(90^o-\alpha)}=2x_vsin(\theta)\)
where \(x_v\) is the radius of circular motion of the particle displace from the \(\psi\) cloud center. The separation between the two rays is,
\(d_b=d.{sin(90^o-\alpha)}=2x_vsin(\theta)\)
Since the particle are reflected off at different times, there is also a phase shift between the lower and upper loop. The \(E\) fields due to the rotating particles on the two loops are both in the same direction. These are linearly polarized light.
When \(\theta\lt90^o-\alpha\),
Both loops leave the second medium at the apex of the cone. There is no phase shift between the two loops. Both loops are reflected off at the point of reflection. The \(E\) fields due to the rotating particles on the two loops radiate from a common center; the ray remains circularly polarized.
Both instances suggest that the cause of such shifts are inherent in the nature of emitted fluorescence and not of the reflecting interface.
Sunday, August 23, 2015
Shield And All Flavors Of Photons.
When \(\small{\beta\to90^o}\), \(\small{\theta\to0^o}\), we see as the aura around a torch on the side of the light source,
If we pulse this emission (\(\small{\beta\to90^o}\)) at an appropriate energy density, \(\psi\) natural frequency, we have a shield that in the absence of a similar energy density field is attractive and in the presence of a similar energy density field repulsive.
This torch emits photons appropriate for the force needed. For example, photons carrying gravitational energy,
The frequency of \(\psi\) around these particles will be high given their size, but the source of this photons can be pulsed to produce an appropriate force field frequency.
But how to create a photon source that is the opposite of a laser; \(\small{\beta\to90^o}\) as oppose to \(\small{\beta\to0^o}\)?
If we pulse this emission (\(\small{\beta\to90^o}\)) at an appropriate energy density, \(\psi\) natural frequency, we have a shield that in the absence of a similar energy density field is attractive and in the presence of a similar energy density field repulsive.
This torch emits photons appropriate for the force needed. For example, photons carrying gravitational energy,
The frequency of \(\psi\) around these particles will be high given their size, but the source of this photons can be pulsed to produce an appropriate force field frequency.
But how to create a photon source that is the opposite of a laser; \(\small{\beta\to90^o}\) as oppose to \(\small{\beta\to0^o}\)?
Saturday, August 22, 2015
Binomial Dispersion
Absorption and emission along the ray, as Huygens' point source can account for dispersion that is binomial,
where the probability of making a turn of \(\beta=90^o-\theta\) is half. The intensity of the ray decreases by \(\small{\left(\cfrac{1}{2}\right)^n}\), \(n\) point source away from the direction of the original ray.
\(\theta\) is polarization.
In the case of a laser, when the \(E\) fields are parallel to the direction of the ray, and \(\small{\theta\to90^o}\), there is no dispersion because \(\small{\beta=0}\).
When the \(E\) fields are perpendicular to the direction of the ray \(\small{\theta\to0}\), light has stop propagating forward and has spread in the direction perpendicular to the initial direction of travel. In this case, \(\small{\beta=90^o}\).
The problem with this view is that the ray attenuates too quickly along the direction of the ray, from point source to point source. Given any light source, there has to be a spread of \(\small{\theta}\) vales such that light that project forward to considerable distance has \(\small{\theta\approx90^o}\), \(\small{\beta\approx0}\).
where the probability of making a turn of \(\beta=90^o-\theta\) is half. The intensity of the ray decreases by \(\small{\left(\cfrac{1}{2}\right)^n}\), \(n\) point source away from the direction of the original ray.
\(\theta\) is polarization.
In the case of a laser, when the \(E\) fields are parallel to the direction of the ray, and \(\small{\theta\to90^o}\), there is no dispersion because \(\small{\beta=0}\).
When the \(E\) fields are perpendicular to the direction of the ray \(\small{\theta\to0}\), light has stop propagating forward and has spread in the direction perpendicular to the initial direction of travel. In this case, \(\small{\beta=90^o}\).
The problem with this view is that the ray attenuates too quickly along the direction of the ray, from point source to point source. Given any light source, there has to be a spread of \(\small{\theta}\) vales such that light that project forward to considerable distance has \(\small{\theta\approx90^o}\), \(\small{\beta\approx0}\).
Friday, August 21, 2015
Huygens' Principle Re-emitted
Repeated absorption and emission of photons provides a physical basis for Huygens' principle, where every point in the path of the light ray is considered a new point source. This "new point source" is the particle that absorbs photons and emits them, along the light ray (wave front).
However, the emission in this case is in the direction perpendicular to the direction of travel of the particle, in either \(\beta=90^o-\theta\) or \(-\beta\), not in all directions perpendicular to a circular wave front.
However, the emission in this case is in the direction perpendicular to the direction of travel of the particle, in either \(\beta=90^o-\theta\) or \(-\beta\), not in all directions perpendicular to a circular wave front.
Pumping position down! Lightly, lightly, lightly!
Then Reflected
From the post "Photon Emission After Absorption" dated 25 Jul 2015, the photon is ejected perpendicular to the direction of travel of the particle; in the post "A Pump!" dated 25 Jul 2015,
\(E_{p}=h.\left\{1-\sqrt{\cfrac{sin(\theta)}{cos(\theta)}}\right\}.f_{cir}\)
when
\(1-\sqrt{\cfrac{sin(\theta)}{cos(\theta)}}\lt0\)
\(\sqrt{\cfrac{sin(\theta)}{cos(\theta)}}\gt1\)
a photon is absorbed first then emitted, this introduces a \(\small{\pi}\) phase in the emission.
The refracted ray we observe in the second medium is made up of emitted photons in the direction perpendicular to \(\alpha_2\) (out of the paper). This emitted ray will be absorbed and be emitted a second time. In the first instance of emission, the photons are emitted perpendicular to the direction of travel of the particle (\(P^{'}O\) and \(PO\)), and is along \(E\,\,PE^{'}\) and \(E\,\,PE\). The direction of incident then changes to from \(PO\) to \(EO\), by a difference of \(90^o-\theta\). Along \(EO\) particles interact with the passing photons, as if along \(PO\).
The ray \(\alpha_2\) corresponds to the line \(EO\). \(EO\) is absorbed and emitted into the direction it was first absorbed. It is diverted by a difference of \(-(90^o-\theta)\) to be along \(PO\) again. Reciprocity.
If we confine photon emission/absorption to be at the point of incident, this emitted ray, \(PO\) will result in a reflected ray,
And the possibility of a phase lag between the absorption of a photon first, then an emission, accounts for the possible \(\pi\) phase shift in the reflected ray.
This is not the reflected ray off a mirrored surface, but reflection from an interface of two mediums with different optical properties. The reflected ray is the result of a second absorption/emission of the photons in the medium, the first absorption/emission allows us to see \(\alpha_2\). The second absorption/emission is due to the interaction of \(\alpha_2\) with the medium. \(\alpha_2\) interacts with the medium only once. The first absorption/emission of the photons in the medium results in the cone \(PE^{'}\,\,E\,\,PE\) from which we started to derive the geometry of \(\alpha_2\) (post "It's All Fluorescence Outside, Inside" dated 29 Jul 2015).
The ray corresponding to \(90^o-\theta_2-\alpha_2\) is probably totally internally reflected. The presence of this ray is important to vindicate the results here. It is possible that not all of this ray is absorbed and emitted to result in a reflected ray.
When would absorption and emission stop? Absorb along \(AB\) \(\to\) emit perpendicularly \(XY\) \(\to\) absorb along \(XY\) \(\to\) emit perpendicularly along \(AB\), return. The photons are emitted in the direction perpendicular to the particle's travel; this is not in the direction perpendicular to the ray on the plane containing the axis of the cone. This emitted ray is rotated about the axis of the cone and reaches an observer perpendicular to the ray out of the paper. It is a cone in 3D in the first place.
And this accounts for a reflected ray, even when \(\alpha_2\) does not penetrate into the second medium.
Note: The cone \(PE^{'}\,\,E\,\,PE\) was not initially conceived from considering absorption and emission. There can be a problem here; two birds with one stone is real luck! The cone accounts for both the direction along the ray and, emitted photons that reach the eyes of the observer, perpendicular to the ray.
Both ray \(-\alpha_2\) and \(90^o-\theta_2-\alpha_2\) are at the point of incident, very small.
\(E_{p}=h.\left\{1-\sqrt{\cfrac{sin(\theta)}{cos(\theta)}}\right\}.f_{cir}\)
when
\(1-\sqrt{\cfrac{sin(\theta)}{cos(\theta)}}\lt0\)
\(\sqrt{\cfrac{sin(\theta)}{cos(\theta)}}\gt1\)
a photon is absorbed first then emitted, this introduces a \(\small{\pi}\) phase in the emission.
The refracted ray we observe in the second medium is made up of emitted photons in the direction perpendicular to \(\alpha_2\) (out of the paper). This emitted ray will be absorbed and be emitted a second time. In the first instance of emission, the photons are emitted perpendicular to the direction of travel of the particle (\(P^{'}O\) and \(PO\)), and is along \(E\,\,PE^{'}\) and \(E\,\,PE\). The direction of incident then changes to from \(PO\) to \(EO\), by a difference of \(90^o-\theta\). Along \(EO\) particles interact with the passing photons, as if along \(PO\).
The ray \(\alpha_2\) corresponds to the line \(EO\). \(EO\) is absorbed and emitted into the direction it was first absorbed. It is diverted by a difference of \(-(90^o-\theta)\) to be along \(PO\) again. Reciprocity.
If we confine photon emission/absorption to be at the point of incident, this emitted ray, \(PO\) will result in a reflected ray,
And the possibility of a phase lag between the absorption of a photon first, then an emission, accounts for the possible \(\pi\) phase shift in the reflected ray.
This is not the reflected ray off a mirrored surface, but reflection from an interface of two mediums with different optical properties. The reflected ray is the result of a second absorption/emission of the photons in the medium, the first absorption/emission allows us to see \(\alpha_2\). The second absorption/emission is due to the interaction of \(\alpha_2\) with the medium. \(\alpha_2\) interacts with the medium only once. The first absorption/emission of the photons in the medium results in the cone \(PE^{'}\,\,E\,\,PE\) from which we started to derive the geometry of \(\alpha_2\) (post "It's All Fluorescence Outside, Inside" dated 29 Jul 2015).
The ray corresponding to \(90^o-\theta_2-\alpha_2\) is probably totally internally reflected. The presence of this ray is important to vindicate the results here. It is possible that not all of this ray is absorbed and emitted to result in a reflected ray.
When would absorption and emission stop? Absorb along \(AB\) \(\to\) emit perpendicularly \(XY\) \(\to\) absorb along \(XY\) \(\to\) emit perpendicularly along \(AB\), return. The photons are emitted in the direction perpendicular to the particle's travel; this is not in the direction perpendicular to the ray on the plane containing the axis of the cone. This emitted ray is rotated about the axis of the cone and reaches an observer perpendicular to the ray out of the paper. It is a cone in 3D in the first place.
And this accounts for a reflected ray, even when \(\alpha_2\) does not penetrate into the second medium.
Note: The cone \(PE^{'}\,\,E\,\,PE\) was not initially conceived from considering absorption and emission. There can be a problem here; two birds with one stone is real luck! The cone accounts for both the direction along the ray and, emitted photons that reach the eyes of the observer, perpendicular to the ray.
Both ray \(-\alpha_2\) and \(90^o-\theta_2-\alpha_2\) are at the point of incident, very small.
Tuesday, August 18, 2015
Once Again Brewster
On closer look at the situation when \(\alpha_{2s}\) and \(\alpha_{2p}\) are perpendicular,
In the second medium,
\(2\theta_1-\Delta\theta-\Delta\alpha=90^o\)
where,
\(\Delta\theta=\theta_1-\theta_2\)
\(\Delta\alpha=\alpha_1-\alpha_2\)
which implies \(2\theta_1\gt90^o\) and so, \(\theta_1\gt45^o\)
So,
\(\theta_1+\theta_2-\alpha_1+\alpha_2=90^o\)
both material properties \(\varepsilon\) and \(n\) are involved. Alternatively,
\(2\theta_1-90^o=\Delta\theta+\Delta\alpha\)
the change in orientation needed, is from both a change in \(\theta\) and \(\alpha\).
When we set,
\(\alpha_1=\theta_1\) --- (1)
then,
\(\theta_2+\alpha_2=90^o\) --- (2)
the ray splits into two perpendicular directions with orthogonal polarization. Given a light source with a spread of values in \(\theta\), there can be a number of \(\theta\) for which a split of the refracted rays orthogonal to each other can occur. Expressions (1) and (2) are the same as those we obtained in the post "Still Looking For Brewster" dated 16 Aug 2015. From that post,
\({ tan(\alpha_1)}{tan(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(\cfrac{ sin^2(\alpha_1)}{cos(\alpha_1)cos(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\)
but \(\alpha_1+\alpha_2\ne90^o\) as oppose to the often quoted \(\alpha_1+\alpha_2=90^o\) in the derivation for Brewster's angle. Instead,
\(sin(\alpha_2)=\cfrac{n_1}{n_2}sin(\alpha_1)\)
\(cos(\alpha_2)=\sqrt{1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)}\)
So,
\(tan(\alpha_1).\cfrac{n_1}{n_2}\cfrac{sin(\alpha_1)}{\sqrt{1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)}}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(tan^2(\alpha_1)sin^2(\alpha_1)=\left(\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\right)^2\left\{1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)\right\}\)
\(tan^2(\alpha_1)sin^2(\alpha_1)+\left(\cfrac{\varepsilon_2}{\varepsilon_1}\right)^2sin^2(\alpha_1)=\left(\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\right)^2\)
In the second medium,
\(2\theta_1-\Delta\theta-\Delta\alpha=90^o\)
where,
\(\Delta\theta=\theta_1-\theta_2\)
\(\Delta\alpha=\alpha_1-\alpha_2\)
which implies \(2\theta_1\gt90^o\) and so, \(\theta_1\gt45^o\)
So,
\(\theta_1+\theta_2-\alpha_1+\alpha_2=90^o\)
both material properties \(\varepsilon\) and \(n\) are involved. Alternatively,
\(2\theta_1-90^o=\Delta\theta+\Delta\alpha\)
the change in orientation needed, is from both a change in \(\theta\) and \(\alpha\).
When we set,
\(\alpha_1=\theta_1\) --- (1)
then,
\(\theta_2+\alpha_2=90^o\) --- (2)
the ray splits into two perpendicular directions with orthogonal polarization. Given a light source with a spread of values in \(\theta\), there can be a number of \(\theta\) for which a split of the refracted rays orthogonal to each other can occur. Expressions (1) and (2) are the same as those we obtained in the post "Still Looking For Brewster" dated 16 Aug 2015. From that post,
\({ tan(\alpha_1)}{tan(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(\cfrac{ sin^2(\alpha_1)}{cos(\alpha_1)cos(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\)
but \(\alpha_1+\alpha_2\ne90^o\) as oppose to the often quoted \(\alpha_1+\alpha_2=90^o\) in the derivation for Brewster's angle. Instead,
\(sin(\alpha_2)=\cfrac{n_1}{n_2}sin(\alpha_1)\)
\(cos(\alpha_2)=\sqrt{1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)}\)
So,
\(tan(\alpha_1).\cfrac{n_1}{n_2}\cfrac{sin(\alpha_1)}{\sqrt{1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)}}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(tan^2(\alpha_1)sin^2(\alpha_1)=\left(\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\right)^2\left\{1-\left(\cfrac{n_1}{n_2}\right)^2sin^2(\alpha_1)\right\}\)
\(tan^2(\alpha_1)sin^2(\alpha_1)+\left(\cfrac{\varepsilon_2}{\varepsilon_1}\right)^2sin^2(\alpha_1)=\left(\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\right)^2\)
\(sin^4(\alpha_1)+\left(\cfrac{\varepsilon_2}{\varepsilon_1}\right)^2sin^2(\alpha_1)(1-sin^2(\alpha_1))=\left(\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\right)^2(1-sin^2(\alpha_1))\)
\(sin^{ 4 }(\alpha _{ 1 })+\left( \cfrac { \varepsilon _{ 2 } }{ \varepsilon _{ 1 } } \right) ^{ 2 }sin^{ 2 }(\alpha _{ 1 })-\left( \cfrac { \varepsilon _{ 2 } }{ \varepsilon _{ 1 } } \right) ^{ 2 }sin^{ 4 }(\alpha _{ 1 })=\left( \cfrac { \varepsilon _{ 2 } }{ \varepsilon _{ 1 } } \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 }-\left( \cfrac { \varepsilon _{ 2 } }{ \varepsilon _{ 1 } } \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 }sin^{ 2 }(\alpha _{ 1 })\)
\( sin^{ 4 }(\alpha _{ 1 })\left\{ 1-\left( \cfrac { \varepsilon _{ 2 } }{ \varepsilon _{ 1 } } \right) ^{ 2 } \right\} +\left( \cfrac { \varepsilon _{ 2 } }{ \varepsilon _{ 1 } } \right) ^{ 2 }\left\{ 1+\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 } \right\} sin^{ 2 }(\alpha _{ 1 })=\left( \cfrac { \varepsilon _{ 2 } }{ \varepsilon _{ 1 } } \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 }\)
\(sin^{ 4 }(\alpha _{ 1 })\left\{ \left( \cfrac { \varepsilon _{ 1 } }{ \varepsilon _{ 2 } } \right) ^{ 2 }-1 \right\} +\left\{ 1+\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 } \right\} sin^{ 2 }(\alpha _{ 1 })=\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 }\)
\(sin^{ 4 }(\alpha _{ 1 })\left\{ \left( \cfrac { \varepsilon _{ 1 } }{ \varepsilon _{ 2 } } \right) ^{ 2 }-1 \right\} +\left\{ 1+\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 } \right\} sin^{ 2 }(\alpha _{ 1 })=\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 }\)
which is quadratic in \(sin^2(\alpha_1)\) and can yield two positive solutions for \(\alpha_1\).
When \(\cfrac { \varepsilon _{ 2 } }{ \varepsilon _{ 1 } }=1\),
\(\left\{ 1+\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 } \right\} sin^{ 2 }(\alpha _{ 1 })=\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 }\)
\(sin^{ 2 }(\alpha _{ 1 })=\frac { \left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 } }{ \left\{ 1+\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 } \right\} }\)
\(tan(\alpha_1)=\cfrac{n_2}{n_1}\)
and this Brewster!
Thank you very much.
When \(\cfrac { \varepsilon _{ 2 } }{ \varepsilon _{ 1 } }=1\),
\(\left\{ 1+\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 } \right\} sin^{ 2 }(\alpha _{ 1 })=\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 }\)
\(sin^{ 2 }(\alpha _{ 1 })=\frac { \left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 } }{ \left\{ 1+\left( \cfrac { n_{ 2 } }{ n_{ 1 } } \right) ^{ 2 } \right\} }\)
and this Brewster!
Thank you very much.
Monday, August 17, 2015
Does Not Look Like What?
From the post "A Bloom Crosses Over" dated 10 Aug 2015,
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(\varepsilon_2\gt\varepsilon_1\)
then,
\(\theta_2\lt\theta_1\)
\(\Delta\theta=\theta_2-\theta_1\lt0\)
In all the previous diagrams \(\Delta\theta\gt0\).
If \(\Delta\theta^{\,'}=-\Delta\theta\)
where \(\varepsilon_2\gt\varepsilon_1\).
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(\varepsilon_2\gt\varepsilon_1\)
then,
\(\theta_2\lt\theta_1\)
\(\Delta\theta=\theta_2-\theta_1\lt0\)
In all the previous diagrams \(\Delta\theta\gt0\).
If \(\Delta\theta^{\,'}=-\Delta\theta\)
where \(\varepsilon_2\gt\varepsilon_1\).
Sunday, August 16, 2015
Still Looking For Brewster
From the post "Late Bloomer Gets The Splits" dated 10 Aug 2015,
\(B_1sin(\alpha_{adj\,\,1})=B_2sin(\alpha_{adj\,\,2})\)
\(\cfrac{B_1}{\mu_1}cos(\alpha_{adj\,\,1})=\cfrac{B_2}{\mu_2}cos(\alpha_{adj\,\,2})\)
\(\alpha_{adj\,\,1}=90^o+\alpha_1-\theta_1\)
\(\alpha_{adj\,\,2}=90^o+\alpha_2-\theta_2\)
but when,
\(\alpha_1=\theta_1\)
\(cos(\alpha_{adj\,\,1})=cos(90^o)=0\)
or when,
\(\alpha_2=\theta_2\)
\(cos(\alpha_{adj\,\,2})=cos(90^o)=0\)
in which case,
\(\mu_1tan(\alpha _{adj\,\, 1 })=\mu_2tan(\alpha _{adj\,\, 2 })\)
is not valid,
The tangential component of the incident ray is zero and the ray enters the medium perpendicular to the inter-surface, parallel to the normal. \(\alpha_{2s}\) passes through the second medium perpendicularly.
In a similar way, when we consider the left arm,
\(B_1sin(\alpha_{adj\,\,1})=B_2sin(\alpha_{adj\,\,2})\)
\(\cfrac{B_1}{\mu_1}cos(\alpha_{adj\,\,1})=\cfrac{B_2}{\mu_2}cos(\alpha_{adj\,\,2})\)
\(\alpha_{adj\,\,1}=\theta_1+\alpha_1-90^o\)
in the first medium, and into the second medium,
\(\alpha_{adj\,\,2}=\theta_2+\alpha_2-90^o\)
If \(\theta_1+\alpha_1=90^o\)
\(sin(\alpha_{adj\,\,1})=sin(0^o)=0\)
or when,
\(B_1sin(\alpha_{adj\,\,1})=B_2sin(\alpha_{adj\,\,2})\)
\(\cfrac{B_1}{\mu_1}cos(\alpha_{adj\,\,1})=\cfrac{B_2}{\mu_2}cos(\alpha_{adj\,\,2})\)
\(\alpha_{adj\,\,1}=90^o+\alpha_1-\theta_1\)
\(\alpha_{adj\,\,2}=90^o+\alpha_2-\theta_2\)
but when,
\(\alpha_1=\theta_1\)
\(cos(\alpha_{adj\,\,1})=cos(90^o)=0\)
or when,
\(\alpha_2=\theta_2\)
\(cos(\alpha_{adj\,\,2})=cos(90^o)=0\)
in which case,
\(\mu_1tan(\alpha _{adj\,\, 1 })=\mu_2tan(\alpha _{adj\,\, 2 })\)
is not valid,
The tangential component of the incident ray is zero and the ray enters the medium perpendicular to the inter-surface, parallel to the normal. \(\alpha_{2s}\) passes through the second medium perpendicularly.
In a similar way, when we consider the left arm,
\(B_1sin(\alpha_{adj\,\,1})=B_2sin(\alpha_{adj\,\,2})\)
\(\cfrac{B_1}{\mu_1}cos(\alpha_{adj\,\,1})=\cfrac{B_2}{\mu_2}cos(\alpha_{adj\,\,2})\)
in the first medium, and into the second medium,
\(\alpha_{adj\,\,2}=\theta_2+\alpha_2-90^o\)
If \(\theta_1+\alpha_1=90^o\)
\(sin(\alpha_{adj\,\,1})=sin(0^o)=0\)
or when,
\(\theta_2+\alpha_2=90^o\)
\(sin(\alpha_{adj\,\,2})=sin(0^o)=0\)
\(sin(\alpha_{adj\,\,2})=sin(0^o)=0\)
the perpendicular component of the left incident arm is zero. The tangential component \(\alpha_{2p}\), glides along the surface (if it is flat) and does not enter the second medium.
Both scenario occurs when,
\(\theta_1=\alpha_1\)
and
\(\theta_2+\alpha_2=90^o\)
The incident ray is split \(90^o\) one along the surface \(\alpha_{2p}\), and the other enters the second medium perpendicularly \(\alpha_{2s}\). This is wrong, velocity along the ray was not accounted for.
This is still not Brewster angle. But, from
\(\theta_2+\alpha_2=90^o\)
\(\theta_2=90^o-\alpha_2\)
\(\theta_1=\alpha_1\)
Since, from the post "A Bloom Crosses Over" dated 10 Aug 2015,
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(\cfrac{ tan(\alpha_1)}{tan(90^o-\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\({ tan(\alpha_1)}{tan(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
From Snell's Law,
\(n_1sin(\alpha_1)=n_2sin(\alpha_2)\)
\(\cfrac{n_1}{n_2}\cfrac{ sin^2(\alpha_1)}{cos(\alpha_1)cos(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
and
\(\cfrac{ sin^2(\alpha_1)}{cos(\alpha_1)cos(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\)
\(\alpha_1+\alpha_2=90^o\) This is wrong!
\(\cfrac{ sin^2(\alpha_1)}{cos(\alpha_1)cos(90^o-\alpha_1)}=\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\)
\(\cfrac{ sin(\alpha_1)}{cos(\alpha_1)}=tan(\alpha_1)=\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\)
which is still not Brewster.
Both scenario occurs when,
\(\theta_1=\alpha_1\)
and
\(\theta_2+\alpha_2=90^o\)
The incident ray is split \(90^o\) one along the surface \(\alpha_{2p}\), and the other enters the second medium perpendicularly \(\alpha_{2s}\). This is wrong, velocity along the ray was not accounted for.
This is still not Brewster angle. But, from
\(\theta_2+\alpha_2=90^o\)
\(\theta_2=90^o-\alpha_2\)
\(\theta_1=\alpha_1\)
Since, from the post "A Bloom Crosses Over" dated 10 Aug 2015,
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(\cfrac{ tan(\alpha_1)}{tan(90^o-\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\({ tan(\alpha_1)}{tan(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
From Snell's Law,
\(n_1sin(\alpha_1)=n_2sin(\alpha_2)\)
\(\cfrac{n_1}{n_2}\cfrac{ sin^2(\alpha_1)}{cos(\alpha_1)cos(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
and
\(\cfrac{ sin^2(\alpha_1)}{cos(\alpha_1)cos(\alpha_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\)
\(\alpha_1+\alpha_2=90^o\) This is wrong!
\(\cfrac{ sin^2(\alpha_1)}{cos(\alpha_1)cos(90^o-\alpha_1)}=\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\)
\(\cfrac{ sin(\alpha_1)}{cos(\alpha_1)}=tan(\alpha_1)=\cfrac{\varepsilon_2}{\varepsilon_1}\cfrac{n_2}{n_1}\)
which is still not Brewster.
Looking for Brewster
When we consider,
\(tan(\theta_2-\alpha^{'}_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha)\)
when \(\theta_1\) is large, such that
\(\theta_1-\alpha\gt90^o\)
Let \(x+90^o=\theta_1-\alpha\) then
\(tan(\theta_1-\alpha)=tan(x+90^o)=-cot(x)\)
So,
\(tan(\theta_2-\alpha^{'}_{2s})=-\cfrac{\mu_2}{\mu_1}cot(\theta_1-\alpha-90^o)\)
\(cot(\theta_2-\alpha^{'}_{2s}+90^o)=\cfrac{\mu_2}{\mu_1}cot(\theta_1-\alpha-90^o)\)
When \(\mu _{ 2 }\gt\mu _{ 1 }\), since \(cot(x)\) is a decreasing function,
\(\theta_2-\alpha^{'}_{2s}+90^o\lt\theta_1-\alpha-90^o\)
\(\alpha^{'}_{2s}\gt180^o+\alpha+\Delta \theta\)
Since the \(\alpha^{'}_{2s}\) has been reflected back into medium 1, \(\Delta \theta=0\),
\(\alpha^{'}_{2s}\gt180^o+\alpha\)
When \(\mu _{ 2 }\lt\mu _{ 1 }\),
\(\theta_2-\alpha^{'}_{2s}+90^o\gt\theta_1-\alpha-90^o\)
\(\alpha^{'}_{2s}\lt180^o+\alpha\)
\(tan(\theta_2+\alpha^{'}_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha)\)
when \(\theta_1\) is large, such that
\(\theta_1+\alpha\gt90^o\)
Let \(x+90^o=\theta_1+\alpha\) then
\(tan(\theta_1+\alpha)=tan(x+90^o)=-cot(x)\)
So,
\(tan(\theta_2+\alpha^{'}_{2p})=-\cfrac{\mu_2}{\mu_1}cot(\theta_1+\alpha-90^o)\)
\(cot(\theta_2+\alpha^{'}_{2p}+90^o)=\cfrac{\mu_2}{\mu_1}cot(\theta_1+\alpha-90^o)\)
When \(\mu _{ 2 }\gt\mu _{ 1 }\),
\(\theta_2+\alpha^{'}_{2p}+90^o\lt\theta_1+\alpha-90^o\)
\(\alpha^{'}_{2p}\lt\alpha-\Delta\theta-180^o\)
Since, \(\Delta\theta=0\)
\(\alpha^{'}_{2p}\) is reflected back along \(\alpha\)
When \(\mu _{ 2 }\lt\mu _{ 1 }\),
\(\theta_2+\alpha^{'}_{2p}+90^o\gt\theta_1+\alpha-90^o\)
\(\alpha^{'}_{2p}\gt\alpha-\Delta\theta-180^o\)
Since, \(\Delta\theta=0\)
When \(\mu _{ 2 }\lt\mu _{ 1 }\), \(\alpha^{'}_{2s}\lt180^o+\alpha\)
When \(\mu _{ 2 }\gt\mu _{ 1 }\), \(\alpha^{'}_{2p}\lt\alpha-180^o\)
When \(\mu _{ 2 }\lt\mu _{ 1 }\), \(\alpha^{'}_{2p}\gt\alpha-180^o\)
\(tan(\theta_2-\alpha^{'}_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha)\)
when \(\theta_1\) is large, such that
\(\theta_1-\alpha\gt90^o\)
Let \(x+90^o=\theta_1-\alpha\) then
\(tan(\theta_1-\alpha)=tan(x+90^o)=-cot(x)\)
So,
\(tan(\theta_2-\alpha^{'}_{2s})=-\cfrac{\mu_2}{\mu_1}cot(\theta_1-\alpha-90^o)\)
\(cot(\theta_2-\alpha^{'}_{2s}+90^o)=\cfrac{\mu_2}{\mu_1}cot(\theta_1-\alpha-90^o)\)
When \(\mu _{ 2 }\gt\mu _{ 1 }\), since \(cot(x)\) is a decreasing function,
\(\theta_2-\alpha^{'}_{2s}+90^o\lt\theta_1-\alpha-90^o\)
\(\alpha^{'}_{2s}\gt180^o+\alpha+\Delta \theta\)
Since the \(\alpha^{'}_{2s}\) has been reflected back into medium 1, \(\Delta \theta=0\),
\(\alpha^{'}_{2s}\gt180^o+\alpha\)
When \(\mu _{ 2 }\lt\mu _{ 1 }\),
\(\theta_2-\alpha^{'}_{2s}+90^o\gt\theta_1-\alpha-90^o\)
\(\alpha^{'}_{2s}\lt180^o+\alpha\)
We can also have,
\(tan(\theta_2+\alpha^{'}_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha)\)
when \(\theta_1\) is large, such that
\(\theta_1+\alpha\gt90^o\)
Let \(x+90^o=\theta_1+\alpha\) then
\(tan(\theta_1+\alpha)=tan(x+90^o)=-cot(x)\)
So,
\(tan(\theta_2+\alpha^{'}_{2p})=-\cfrac{\mu_2}{\mu_1}cot(\theta_1+\alpha-90^o)\)
\(cot(\theta_2+\alpha^{'}_{2p}+90^o)=\cfrac{\mu_2}{\mu_1}cot(\theta_1+\alpha-90^o)\)
When \(\mu _{ 2 }\gt\mu _{ 1 }\),
\(\theta_2+\alpha^{'}_{2p}+90^o\lt\theta_1+\alpha-90^o\)
\(\alpha^{'}_{2p}\lt\alpha-\Delta\theta-180^o\)
Since, \(\Delta\theta=0\)
\(\alpha^{'}_{2p}\lt\alpha-180^o\)
When \(\mu _{ 2 }\lt\mu _{ 1 }\),
\(\theta_2+\alpha^{'}_{2p}+90^o\gt\theta_1+\alpha-90^o\)
\(\alpha^{'}_{2p}\gt\alpha-\Delta\theta-180^o\)
Since, \(\Delta\theta=0\)
\(\alpha^{'}_{2p}\gt\alpha-180^o\)
This might seem to be the same results as the post "More Bending Of Light" dated 13 Aug 2015, but the swing of \(\alpha_s\) and \(\alpha_p\) are different,
When \(\mu _{ 2 }\gt\mu _{ 1 }\), \(\alpha^{'}_{2s}\gt180^o+\alpha\)
When \(\mu _{ 2 }\lt\mu _{ 1 }\), \(\alpha^{'}_{2p}\gt\alpha-180^o\)
Previously,
When \(\mu_2\gt\mu_1\), \(\alpha_{2s}\lt-180^o+\alpha\)
When \(\mu_2\lt\mu_1\), \(\alpha_{2s}\gt-180^o+\alpha\)
This cases show the swing of \(\alpha_{2s}\) and \(\alpha_{2p}\) as \(\theta_1\) changed. There is no Brewster angle here.
Decreasing Polarization Was Common Sense
Ooops,
The angle was assigned wrongly in the post "A Bloom Crosses Over" dated 10 Aug 2015.
It should have been,
\(\beta=90^o-\theta\)
and so,
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
as the cone spreads, \(\beta\) increases but \(\theta\) decreases. And when,
\(\varepsilon_1\lt\varepsilon_2\)
\(\theta_1\gt\theta_2\)
polarization decreases.
This is then consistent with post "On Reflection Radar Theory 101" dated 16 Aug 2015, where the horizontal component of \(E\) attenuates and \(\theta\) decreases.
Which proves common sense is rare.
The angle was assigned wrongly in the post "A Bloom Crosses Over" dated 10 Aug 2015.
It should have been,
\(\beta=90^o-\theta\)
and so,
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
as the cone spreads, \(\beta\) increases but \(\theta\) decreases. And when,
\(\varepsilon_1\lt\varepsilon_2\)
\(\theta_1\gt\theta_2\)
polarization decreases.
This is then consistent with post "On Reflection Radar Theory 101" dated 16 Aug 2015, where the horizontal component of \(E\) attenuates and \(\theta\) decreases.
Which proves common sense is rare.
On Reflection Radar Theory 101
From the post "Turning With The Rest Of Us" and "More Bending Of Light" both dated 13 Aug 2015, when
\(\theta_1-\alpha\lt0\)
For \(\mu_2\lt\mu_1\),
\(\alpha_{2s}\gt-180^o+\alpha\)
and \(\mu_2\gt\mu_1\),
\(\alpha_{2s}\lt-180^o+\alpha\)
The reflected ray, \(\alpha_{2s}\) can be steered by changing \(\mu_2\),
\(tan(\theta_2-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha)\)
\(\alpha_{2s}\) being reflected by rotating \(-180^o\).
\(\theta_1=\theta_2\)
\(tan(\theta_1-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha)\)
This is important in the case of \(EMW\) where a reflector opposite to an emitting source focuses the radiation behind the source.
In the case of a perfect conductor, \(\alpha_{2p}\) does not exist as there cannot be magnetic fields inside the conductor. \(\alpha_{2p}\) is absorbed by the conductor; half of the energy in the wave is absorbed. If \(\theta\) is kept small, the vertical component of the \(E\) field is small compared to the horizontal component in the direction of travel of the radiation. This horizontal component attenuates as the wave move into medium of varying \(\varepsilon\); the vertical component remained unchanged. \(\theta\) should be kept large \(\theta\to90^o\) as \(\alpha_{2s}\) only depends on \(\alpha\), \(\mu_2\) and \(\mu_1\), up to the range over which the horizontal component of \(E\) attenuates completely. As the wave attenuates, \(\theta\) decreases and is more readily reflected given the incident angle \(\alpha\).
Apart from keeping polarization high, \(\Delta\theta\) dose not effect \(\alpha_{2s}\), the reflected EMW.
\(\theta_1-\alpha\lt0\)
For \(\mu_2\lt\mu_1\),
\(\alpha_{2s}\gt-180^o+\alpha\)
and \(\mu_2\gt\mu_1\),
\(\alpha_{2s}\lt-180^o+\alpha\)
The reflected ray, \(\alpha_{2s}\) can be steered by changing \(\mu_2\),
\(tan(\theta_2-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha)\)
\(\alpha_{2s}\) being reflected by rotating \(-180^o\).
\(\theta_1=\theta_2\)
\(tan(\theta_1-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha)\)
This is important in the case of \(EMW\) where a reflector opposite to an emitting source focuses the radiation behind the source.
In the case of a perfect conductor, \(\alpha_{2p}\) does not exist as there cannot be magnetic fields inside the conductor. \(\alpha_{2p}\) is absorbed by the conductor; half of the energy in the wave is absorbed. If \(\theta\) is kept small, the vertical component of the \(E\) field is small compared to the horizontal component in the direction of travel of the radiation. This horizontal component attenuates as the wave move into medium of varying \(\varepsilon\); the vertical component remained unchanged. \(\theta\) should be kept large \(\theta\to90^o\) as \(\alpha_{2s}\) only depends on \(\alpha\), \(\mu_2\) and \(\mu_1\), up to the range over which the horizontal component of \(E\) attenuates completely. As the wave attenuates, \(\theta\) decreases and is more readily reflected given the incident angle \(\alpha\).
Apart from keeping polarization high, \(\Delta\theta\) dose not effect \(\alpha_{2s}\), the reflected EMW.
Friday, August 14, 2015
Old Friends
If \(\mu\) is to \(B\) as \(\varepsilon\) is to \(E\), what then is \(n\) to? Why, in the first place photons reduce velocity?
\(v^2=\cfrac{1}{\mu\varepsilon}\)
\(\cfrac{v^2_1}{v^2_2}=\cfrac{\mu_2\varepsilon_2}{\mu_1\varepsilon_1}\)
Since,
\(c^2=\cfrac{1}{\mu_o\varepsilon_o}\)
If we define,
\(n_o=\sqrt{\mu_o\varepsilon_o}\)
then,
\(n_r=\cfrac{n}{n_o}=\sqrt{\cfrac{\mu\varepsilon}{\mu_o\varepsilon_o}}\)
\(n_r=\cfrac{1}{v\sqrt{\mu_o\varepsilon_o}}\)
\(n_r.v=c\)
\(n\) is the result of both \(\mu\) on \(B\) and \(\varepsilon\) on \(E\). \(n_r\) is defined relative to \(c\), or \(\small{\sqrt{\mu_o\varepsilon_o}}\)
\(v^2=\cfrac{1}{\mu\varepsilon}\)
\(\cfrac{v^2_1}{v^2_2}=\cfrac{\mu_2\varepsilon_2}{\mu_1\varepsilon_1}\)
Since,
\(c^2=\cfrac{1}{\mu_o\varepsilon_o}\)
If we define,
\(n_o=\sqrt{\mu_o\varepsilon_o}\)
then,
\(n_r=\cfrac{n}{n_o}=\sqrt{\cfrac{\mu\varepsilon}{\mu_o\varepsilon_o}}\)
\(n_r=\cfrac{1}{v\sqrt{\mu_o\varepsilon_o}}\)
\(n_r.v=c\)
\(n\) is the result of both \(\mu\) on \(B\) and \(\varepsilon\) on \(E\). \(n_r\) is defined relative to \(c\), or \(\small{\sqrt{\mu_o\varepsilon_o}}\)
Thursday, August 13, 2015
Turning With The Rest Of Us?
Cont'd from the previous post "More Bending of Light",
When we superimpose the effect of refraction, is \(\alpha_{2s}\) in the first medium along \(\alpha_1\) or along \(\alpha_2\) rotated by \(180^o\)?
In the second medium, \(\alpha_2\) is rotated.
When we superimpose the effect of refraction, is \(\alpha_{2s}\) in the first medium along \(\alpha_1\) or along \(\alpha_2\) rotated by \(180^o\)?
In the second medium, \(\alpha_2\) is rotated.
More Bending Of Light
From the post "Split Cannot Mend" dated 10 Aug 2015,
\(tan(\theta_2-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha)\)
when
\(\theta_1-\alpha\lt0\)
ie incident angle \(\alpha\) large,
\(tan(\theta_2-\alpha_{2s})=-\cfrac{\mu_2}{\mu_1}tan(\alpha-\theta_1)\)
\(tan(\theta_2-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(180^o-\alpha+\theta_1)\)
When \(\mu_2\lt\mu_1\),
\(\theta_2-\alpha_{2s}\lt180^o-\alpha+\theta_1\)
\(\alpha_{2s}\gt\Delta \theta-180^o+\alpha\)
But if \(\alpha_{2s}\) is to make a turn of \(-180^o\),
\(\theta_2=\theta_1\)
\(\Delta \theta=0\)
And so,
\(\alpha_{2s}\gt-180^o+\alpha\)
Also consider when \(\mu_2\gt\mu_1\),
\(\theta_2-\alpha_{2s}\gt180^o-\alpha+\theta_1\)
\(\alpha_{2s}\lt\Delta \theta-180^o+\alpha\)
But if \(\alpha_{2s}\) is to make a turn of \(-180^o\),
\(\theta_2=\theta_1\)
\(\Delta \theta=0\)
And so,
\(\alpha_{2s}\lt-180^o+\alpha\)
So, when \(\mu_2=\mu_1\)
\(\alpha_{2s}=-180^o+\alpha\)
\(\alpha_{2s}\) is reflected back along \(\alpha\), as \(\alpha_{2s}\) is measured anticlockwise positive. In all cases, \(\alpha_{2s}\) is reflected back into in medium \(\mu_1\).
When we consider,
\(tan(\theta_2+\alpha_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha)\)
for large incident angle \(\alpha\), such that
\(\theta_1+\alpha\gt180^o\)
This happens with \(\small{EMW}\) where \(\theta\) is measured towards the positive \(E\) direction.
Let \(x+180^o=\theta_1+\alpha\) then
\(tan(\theta_1+\alpha)=tan(x+180^o)=tan(x)\)
So,
\(tan(\theta_2+\alpha_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha-180^o)\)
\(tan(180^o+\theta_2+\alpha_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha-180^o)\)
When \(\mu_2\lt\mu_1\),
\(180^o+\theta_2+\alpha_{2p}\lt\theta_1+\alpha-180^o\)
\(\alpha_{2p}\lt-360^o-\Delta\theta+\alpha\)
and when \(\mu_2\gt\mu_1\),
\(180^o+\theta_2+\alpha_{2p}\gt\theta_1+\alpha-180^o\)
\(\alpha_{2p}\gt-360^o-\Delta\theta+\alpha\)
In these cases, \(\alpha_{2p}\) is not in the same medium.
The two beams \(\alpha_{2s}\) and \(\alpha_{2p}\) behave differently for large incident angle \(\alpha\). \(\alpha_{2s}\) is reflected back along \(\alpha\), the incident ray and \(\alpha_{2p}\) is displaced from the extrapolated path of \(\alpha\) by \(-\Delta \theta\).
Total internal reflection due to velocity changes as photons pass through the two mediums is a distinct phenomenon apart from these.
\(tan(\theta_2-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha)\)
when
\(\theta_1-\alpha\lt0\)
ie incident angle \(\alpha\) large,
\(tan(\theta_2-\alpha_{2s})=-\cfrac{\mu_2}{\mu_1}tan(\alpha-\theta_1)\)
\(tan(\theta_2-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(180^o-\alpha+\theta_1)\)
When \(\mu_2\lt\mu_1\),
\(\theta_2-\alpha_{2s}\lt180^o-\alpha+\theta_1\)
\(\alpha_{2s}\gt\Delta \theta-180^o+\alpha\)
But if \(\alpha_{2s}\) is to make a turn of \(-180^o\),
\(\theta_2=\theta_1\)
\(\Delta \theta=0\)
And so,
\(\alpha_{2s}\gt-180^o+\alpha\)
Also consider when \(\mu_2\gt\mu_1\),
\(\theta_2-\alpha_{2s}\gt180^o-\alpha+\theta_1\)
\(\alpha_{2s}\lt\Delta \theta-180^o+\alpha\)
But if \(\alpha_{2s}\) is to make a turn of \(-180^o\),
\(\theta_2=\theta_1\)
\(\Delta \theta=0\)
And so,
\(\alpha_{2s}\lt-180^o+\alpha\)
So, when \(\mu_2=\mu_1\)
\(\alpha_{2s}=-180^o+\alpha\)
\(\alpha_{2s}\) is reflected back along \(\alpha\), as \(\alpha_{2s}\) is measured anticlockwise positive. In all cases, \(\alpha_{2s}\) is reflected back into in medium \(\mu_1\).
\(tan(\theta_2+\alpha_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha)\)
for large incident angle \(\alpha\), such that
\(\theta_1+\alpha\gt180^o\)
This happens with \(\small{EMW}\) where \(\theta\) is measured towards the positive \(E\) direction.
Let \(x+180^o=\theta_1+\alpha\) then
\(tan(\theta_1+\alpha)=tan(x+180^o)=tan(x)\)
So,
\(tan(\theta_2+\alpha_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha-180^o)\)
\(tan(180^o+\theta_2+\alpha_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha-180^o)\)
When \(\mu_2\lt\mu_1\),
\(180^o+\theta_2+\alpha_{2p}\lt\theta_1+\alpha-180^o\)
\(\alpha_{2p}\lt-360^o-\Delta\theta+\alpha\)
\(180^o+\theta_2+\alpha_{2p}\gt\theta_1+\alpha-180^o\)
\(\alpha_{2p}\gt-360^o-\Delta\theta+\alpha\)
In these cases, \(\alpha_{2p}\) is not in the same medium.
The two beams \(\alpha_{2s}\) and \(\alpha_{2p}\) behave differently for large incident angle \(\alpha\). \(\alpha_{2s}\) is reflected back along \(\alpha\), the incident ray and \(\alpha_{2p}\) is displaced from the extrapolated path of \(\alpha\) by \(-\Delta \theta\).
Total internal reflection due to velocity changes as photons pass through the two mediums is a distinct phenomenon apart from these.
Wednesday, August 12, 2015
All Mathematical Interpretations Are Fiction
Consider the \(\psi\) of a particle expanding from \(x=x_a\) to \(x=x_c\), \(\psi\) is at velocity \(c\) along \(ix\), the gain in energy is,
\(\Delta E=E_{x_c}-E_{x_a}=2\pi x_cmc-2\pi x_amc\)
But,
\(\Delta E=\bar F.\Delta x=2\pi mc(x_c-x_a)\)
so,
\(\bar F=2\pi mc\)
We know that,
\(F=-\psi\)
where \(F\) the Newtonian force due to \(\psi\). The average force on \(\psi\) is,
\(\bar F =-(-\bar \psi)=\bar\psi=2\pi mc\)
as the particle's \(\psi\) expanded from \(x_a\) to \(x_c\). Through out this process \(KE=\cfrac{1}{2}mc^2\) remains unchanged.
The average acceleration,
\(\bar a_c=2\pi c\)
Since the particle is in circular motion, and \(\bar F\) is along a radial line,
\(\bar F=2\pi c=\cfrac{c^2}{\bar x}\)
and
\(\bar x=\cfrac{c}{2\pi}\)
What is \(\bar x\)? \(\bar F\) is a hypothetical average force, that extends up to \(\bar x\) and is zero beyond. But be warned, all mathematical interpretations are fiction next to bullshit. Bullshit on the other hand, bulls will testify, is for real.
Have a nice day.
\(\Delta E=E_{x_c}-E_{x_a}=2\pi x_cmc-2\pi x_amc\)
But,
\(\Delta E=\bar F.\Delta x=2\pi mc(x_c-x_a)\)
so,
\(\bar F=2\pi mc\)
We know that,
\(F=-\psi\)
where \(F\) the Newtonian force due to \(\psi\). The average force on \(\psi\) is,
\(\bar F =-(-\bar \psi)=\bar\psi=2\pi mc\)
as the particle's \(\psi\) expanded from \(x_a\) to \(x_c\). Through out this process \(KE=\cfrac{1}{2}mc^2\) remains unchanged.
The average acceleration,
\(\bar a_c=2\pi c\)
Since the particle is in circular motion, and \(\bar F\) is along a radial line,
\(\bar F=2\pi c=\cfrac{c^2}{\bar x}\)
and
\(\bar x=\cfrac{c}{2\pi}\)
What is \(\bar x\)? \(\bar F\) is a hypothetical average force, that extends up to \(\bar x\) and is zero beyond. But be warned, all mathematical interpretations are fiction next to bullshit. Bullshit on the other hand, bulls will testify, is for real.
Have a nice day.
The Trouble With Being The Same Color
Reconciliation is easier with one common goal, but...
The particle is a standing wave along its circular path. Given \(x_c\), each \(x_d\) makes a unique angle \(\theta\). The spread of \(\theta\) depended on the range of \(x_d\) which in turn depends on the value of \(v^2_{min}\) from \(c^2\). (Post "A Pump!" dated 25 Jul 2015.) At \(v^2_{min}\) and \(x=x_{min}\) is the orbit of the particle at its lowest \(KE\), but at the furthest point on its oscillation path.
We have a wave of lowest \(KE\) around a circle of radius \(x_{min}\),
\(2\pi x_{min}=n\lambda_{min}\)
This wavelength, \(\lambda_{min}\) is likely to be the wavelength we associate color with. Valid values of \(x\) around \(x_{min}\) spread the color spectrum on both sides of \(x_{min}\). For each value of \(x\) there is a unique value for \(\theta\).
The particle is in a helical path of radius \(x_c\). The specific motion along \(\small{2\pi x_c}\) is changed, but \(x_d\) that indicates oscillation remains unchanged and the wavelength we associate color with is still \(\lambda_{min}\).
In both cases, they are still de Broglie standing wave of radius \(x_{min}\).
This explanation allows for two different material of different energies at the quantum level to have the same color. And it allows for the finite spectrum width of the emission from a laser, otherwise the emission spectrum from a laser associated with one energy level change is a very sharp line.
Note: \(2\pi x_c=n\lambda\) serve to illustrate de Broglie standing wave. The actual standing wave that we associate color with is at \(v^2_{min}\) with \(x=x_{min}\).
It does not matter whether the particle has a wave or a helical path around \(x_c\), for the discussion so far. The helical path gives the particle a spin.
The particle is a standing wave along its circular path. Given \(x_c\), each \(x_d\) makes a unique angle \(\theta\). The spread of \(\theta\) depended on the range of \(x_d\) which in turn depends on the value of \(v^2_{min}\) from \(c^2\). (Post "A Pump!" dated 25 Jul 2015.) At \(v^2_{min}\) and \(x=x_{min}\) is the orbit of the particle at its lowest \(KE\), but at the furthest point on its oscillation path.
We have a wave of lowest \(KE\) around a circle of radius \(x_{min}\),
\(2\pi x_{min}=n\lambda_{min}\)
This wavelength, \(\lambda_{min}\) is likely to be the wavelength we associate color with. Valid values of \(x\) around \(x_{min}\) spread the color spectrum on both sides of \(x_{min}\). For each value of \(x\) there is a unique value for \(\theta\).
The particle is in a helical path of radius \(x_c\). The specific motion along \(\small{2\pi x_c}\) is changed, but \(x_d\) that indicates oscillation remains unchanged and the wavelength we associate color with is still \(\lambda_{min}\).
In both cases, they are still de Broglie standing wave of radius \(x_{min}\).
This explanation allows for two different material of different energies at the quantum level to have the same color. And it allows for the finite spectrum width of the emission from a laser, otherwise the emission spectrum from a laser associated with one energy level change is a very sharp line.
Note: \(2\pi x_c=n\lambda\) serve to illustrate de Broglie standing wave. The actual standing wave that we associate color with is at \(v^2_{min}\) with \(x=x_{min}\).
It does not matter whether the particle has a wave or a helical path around \(x_c\), for the discussion so far. The helical path gives the particle a spin.
Birefringence Going Colorful
Cont'd from the post "In Colors", dated 11 Aug 2015,
Color dispersion is not birefringence, the spread of color is due to the spread of values of \(\theta\) in the light source that results in a spread of values in \(\Delta \theta\).
However, when the source is monochromatic, the ray will split as a result of \(\Delta\theta\). A single mono color dot will appear as two dots looking into the direction of refraction. This is birefringence. \(\Delta \theta\) is due to applying boundary conditions on \(B\) as in the post "A Bloom Crosses Over" dated 10 Aug 2015, where,
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(\varepsilon_1\), \(\varepsilon_2\) are electric permittivity.
Embedded charges in the material that changes \(\varepsilon\) will change \(\Delta \theta\) locally and possibly result in color patterns when illuminated with white light.
Birefringence and color dispersion may have the same underlying mechanism, but the factor leading to their manifestation is different. Color dispersion further requires a spread of \(\theta\).
\(B\) does not appear in the expressions for \(\alpha_{2s}\) and \(\alpha_{2p}\), as long as \(B\ne0\) both expressions are valid. Since in color dispersion, both \(\alpha_{2s}\) and \(\alpha_{2p}\) depended on color, \(B\) is not color.
The problem is, does turning a polarizer in white light let different color light through at different polarizing angle?
No, a polarizer is in fluorescence. Photons at different \(\theta\) are absorbed and emitted according to an emission distribution. This emission distribution has two dominant modes about \(\small{90^o}\) apart. (post "Not Exactly A Fluorescence Polarizer" dated 28 Jul 2015) . The color of the absorbed photons are destroyed. Colors are redistributed according to the emission distribution of the polarizer convoluted with the source color \(\theta\) distribution.
Unless photon absorption is selective based on \(\theta\), ie not a uniform distribution of \(\theta\) as assumed in the post "Not Exactly A Fluorescence Polarizer" dated 28 Jul 2015, then the emission distribution will be the convolution of the source distribution with the absorption distribution, and then the result convoluted with the emission distribution based on a uniformly distributed \(\theta\).
Colors are destroyed in a polarizer.
How then do we reconcile frequency/wavelength and \(\theta\)?
Tomorrow then...
Color dispersion is not birefringence, the spread of color is due to the spread of values of \(\theta\) in the light source that results in a spread of values in \(\Delta \theta\).
However, when the source is monochromatic, the ray will split as a result of \(\Delta\theta\). A single mono color dot will appear as two dots looking into the direction of refraction. This is birefringence. \(\Delta \theta\) is due to applying boundary conditions on \(B\) as in the post "A Bloom Crosses Over" dated 10 Aug 2015, where,
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
\(\varepsilon_1\), \(\varepsilon_2\) are electric permittivity.
Embedded charges in the material that changes \(\varepsilon\) will change \(\Delta \theta\) locally and possibly result in color patterns when illuminated with white light.
Birefringence and color dispersion may have the same underlying mechanism, but the factor leading to their manifestation is different. Color dispersion further requires a spread of \(\theta\).
\(B\) does not appear in the expressions for \(\alpha_{2s}\) and \(\alpha_{2p}\), as long as \(B\ne0\) both expressions are valid. Since in color dispersion, both \(\alpha_{2s}\) and \(\alpha_{2p}\) depended on color, \(B\) is not color.
The problem is, does turning a polarizer in white light let different color light through at different polarizing angle?
No, a polarizer is in fluorescence. Photons at different \(\theta\) are absorbed and emitted according to an emission distribution. This emission distribution has two dominant modes about \(\small{90^o}\) apart. (post "Not Exactly A Fluorescence Polarizer" dated 28 Jul 2015) . The color of the absorbed photons are destroyed. Colors are redistributed according to the emission distribution of the polarizer convoluted with the source color \(\theta\) distribution.
Unless photon absorption is selective based on \(\theta\), ie not a uniform distribution of \(\theta\) as assumed in the post "Not Exactly A Fluorescence Polarizer" dated 28 Jul 2015, then the emission distribution will be the convolution of the source distribution with the absorption distribution, and then the result convoluted with the emission distribution based on a uniformly distributed \(\theta\).
Colors are destroyed in a polarizer.
How then do we reconcile frequency/wavelength and \(\theta\)?
Tomorrow then...
Tuesday, August 11, 2015
In Colors
When \(\mu_2\gt\mu_1\) and \(\theta\) spread continuously over a range of vales,
Rays of different \(\theta\) spread between \(\alpha_2+\Delta\theta\) and \(\alpha_2-\Delta\theta\), equally on both sides of \(\alpha_2\).
From which we conclude color is \(\theta\) and white light has a spread of continuous \(\theta\). Two factors contribute to the spread: change in velocity on crossing into the medium and boundary conditions on \(B\) at the medium boundary.
These factors allows for different colored light to have the same velocity in the second medium and still be refracted to a different refraction angle resulting in the spread of colors. By Snell's Law alone different color lights have different refractive indices and have different velocities in the second medium in order to account for color dispersion.
Rays of different \(\theta\) spread between \(\alpha_2+\Delta\theta\) and \(\alpha_2-\Delta\theta\), equally on both sides of \(\alpha_2\).
From which we conclude color is \(\theta\) and white light has a spread of continuous \(\theta\). Two factors contribute to the spread: change in velocity on crossing into the medium and boundary conditions on \(B\) at the medium boundary.
These factors allows for different colored light to have the same velocity in the second medium and still be refracted to a different refraction angle resulting in the spread of colors. By Snell's Law alone different color lights have different refractive indices and have different velocities in the second medium in order to account for color dispersion.
They Did It Together
When we superimpose both the effects of change in speed along the direction of incidence, that gives us Snell's Law and boundary conditions applied to the \(B\) field at the medium interface, we have,
\(\alpha\to\alpha_2\)
For the case of \(\mu_2\gt\mu_1\),
\(\alpha_{2s}\lt\alpha_2+\Delta\theta\)
and
\(\alpha_{2p}\gt\alpha_2-\Delta\theta\)
For the case of \(\mu_2\lt\mu_1\),
\(\alpha_{2s}\gt\alpha_2+\Delta\theta\)
and
\(\alpha_{2p}\lt\alpha_2-\Delta\theta\)
When \(\Delta \theta=0\), the equations collapse to
\(\alpha_{2s}=\alpha_{2p}=\alpha_2\)
as we observe by Snell's Law for refraction alone. (We take the intersection of the two regions defining \(\alpha_{2s}\) and \(\alpha_{2p}\) after admitting the case of \(\mu_1=\mu_2\). )
It might appear that the split is due to the change in polarization \(\theta\) alone. In fact, both polarization, \(\theta\) and boundary conditions for the \(B\) field at the interface, contribute to refraction.
Note: \(\mu\ne n\)
\(\alpha\to\alpha_2\)
For the case of \(\mu_2\gt\mu_1\),
\(\alpha_{2s}\lt\alpha_2+\Delta\theta\)
and
\(\alpha_{2p}\gt\alpha_2-\Delta\theta\)
For the case of \(\mu_2\lt\mu_1\),
\(\alpha_{2s}\gt\alpha_2+\Delta\theta\)
and
\(\alpha_{2p}\lt\alpha_2-\Delta\theta\)
When \(\Delta \theta=0\), the equations collapse to
\(\alpha_{2s}=\alpha_{2p}=\alpha_2\)
as we observe by Snell's Law for refraction alone. (We take the intersection of the two regions defining \(\alpha_{2s}\) and \(\alpha_{2p}\) after admitting the case of \(\mu_1=\mu_2\). )
It might appear that the split is due to the change in polarization \(\theta\) alone. In fact, both polarization, \(\theta\) and boundary conditions for the \(B\) field at the interface, contribute to refraction.
Note: \(\mu\ne n\)
They Swing
Cont'd from "Left Side, Right Side, Bounded And Kinky" dated 10 Aug 2015,
For the case of \(\mu_2\gt\mu_1\),
\(\alpha_{2s}\lt\alpha+\Delta\theta\)
and
\(\alpha_{2p}\gt\alpha-\Delta\theta\)
It is possible that \(\alpha_{2s}\) crosses below \(\alpha_{2p}\) when \(\Delta\theta\lt0\). \(\alpha_{2s}\) is not necessarily the left beam. \(\Delta\theta\) can be adjusted to swing the beams over \(\alpha\).
For the case of \(\mu_2\gt\mu_1\),
\(\alpha_{2s}\lt\alpha+\Delta\theta\)
and
\(\alpha_{2p}\gt\alpha-\Delta\theta\)
It is possible that \(\alpha_{2s}\) crosses below \(\alpha_{2p}\) when \(\Delta\theta\lt0\). \(\alpha_{2s}\) is not necessarily the left beam. \(\Delta\theta\) can be adjusted to swing the beams over \(\alpha\).
Monday, August 10, 2015
Left Side, Right Side, Bounded And Kinky
Looking at the results from the post "Split Cannot Mend" dated 10 Aug 2015, what happen when,
\(\theta_2-\alpha_{2s}\lt0^o\)
and
\(\theta_2+\alpha_{2p}\gt90^o\) ??
And when \(\mu_2\gt\mu_1\)
\(\theta_2-\alpha_{2s}\gt\theta_1-\alpha\)
\(\alpha_{2s}\lt\theta_2-\theta_1+\alpha\)
and
\(\theta_2+\alpha_{2p}\gt\theta_1+\alpha\)
\(\alpha_{2p}\gt\alpha-(\theta_2-\theta_1)\)
If we define,
\(\Delta \theta=\theta_2-\theta_1\)
\(\alpha_{2s}\lt\alpha+\Delta\theta\)
and
\(\alpha_{2p}\gt\alpha-\Delta\theta\)
and the split occurs on the two sides about \(\alpha\) through the foot of the surface normal bounded by \(\pm\Delta \theta\)
When \(\mu_2\lt\mu_1\)
\(\theta_2-\alpha_{2s}\lt0^o\)
and
\(\theta_2+\alpha_{2p}\gt90^o\) ??
And when \(\mu_2\gt\mu_1\)
\(\theta_2-\alpha_{2s}\gt\theta_1-\alpha\)
\(\alpha_{2s}\lt\theta_2-\theta_1+\alpha\)
and
\(\theta_2+\alpha_{2p}\gt\theta_1+\alpha\)
\(\alpha_{2p}\gt\alpha-(\theta_2-\theta_1)\)
If we define,
\(\Delta \theta=\theta_2-\theta_1\)
\(\alpha_{2s}\lt\alpha+\Delta\theta\)
and
\(\alpha_{2p}\gt\alpha-\Delta\theta\)
and the split occurs on the two sides about \(\alpha\) through the foot of the surface normal bounded by \(\pm\Delta \theta\)
When \(\mu_2\lt\mu_1\)
\(\theta_2-\alpha_{2s}\lt\theta_1-\alpha\)
\(\alpha_{2s}\gt\alpha+\Delta \theta\)
and
\(\theta_2+\alpha_{2p}\lt\theta_1+\alpha\)
\(\alpha_{2p}\lt\alpha-\Delta \theta\)
Split Cannot Mend
Consider this,
\(\cfrac{\mu_2}{\mu_1}=\cfrac{tan(\theta_2-\alpha_{2s})}{tan(\theta_1-\alpha)}=\cfrac{tan(\theta_2+\alpha_{2p})}{tan(\theta_1+\alpha)}\)
\(tan(\theta_2-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha) \)
from which we may obtain \(\alpha_{2s}\). And
\(tan(\theta_2+\alpha_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha) \)
from which we may obtain \(\alpha_{2p}\).
And \(\theta_2\) is given by,
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
from the post "A Bloom Crosses Over" dated 10 Aug 2015.
The graph illustrates how to obtain \(\alpha_{2s}\) and \(\alpha_{2p}\).
\(\cfrac{\mu_2}{\mu_1}=\cfrac{tan(\theta_2-\alpha_{2s})}{tan(\theta_1-\alpha)}=\cfrac{tan(\theta_2+\alpha_{2p})}{tan(\theta_1+\alpha)}\)
\(tan(\theta_2-\alpha_{2s})=\cfrac{\mu_2}{\mu_1}tan(\theta_1-\alpha) \)
from which we may obtain \(\alpha_{2s}\). And
\(tan(\theta_2+\alpha_{2p})=\cfrac{\mu_2}{\mu_1}tan(\theta_1+\alpha) \)
from which we may obtain \(\alpha_{2p}\).
And \(\theta_2\) is given by,
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
from the post "A Bloom Crosses Over" dated 10 Aug 2015.
The graph illustrates how to obtain \(\alpha_{2s}\) and \(\alpha_{2p}\).
Late Bloomer Gets The Splits
In the post "A Bloom Crosses Over" dated 10 Aug 2015, we have only considered the right edge of the cone. The left edge is refracted differently. Consider first, the left edge of the cone passing into the medium last,
since the base is perpendicular to the direction of incident, there is no need to adjust for \(\alpha\),
\(\cfrac { AB }{ v_{ 1 } } =\cfrac { A^{ ' }B^{ ' } }{ v_{ 2 } }\)
Since \(BA^{'}\) is common,
\(\cfrac {BA^{'} sin(\alpha _{1 }) }{ v_{ 1 } } =\cfrac {BA^{'} sin(\alpha _{ 2 }) }{ v_{ 2 } }\)
And
\(n.v=c\)
\(n\propto\cfrac{1}{v}\)
We have,
\(n_1sin(\alpha _{1 }) =n_2sin(\alpha _{ 2 }) \)
which is exactly Snell's Law. This is so, if the only factor resulting in refraction is the change in speed along the direction of incidence. We also have to consider how the \(B\) field behave at the interface.
When we consider the boundary conditions for the analogous \(B\) field on the right side of the cone, we have still,
\(B_1sin(\alpha_{adj\,\,1})=B_2sin(\alpha_{adj\,\,2})\)
\(\cfrac{B_1}{\mu_1}cos(\alpha_{adj\,\,1})=\cfrac{B_2}{\mu_2}cos(\alpha_{adj\,\,2})\)
\(\mu_1tan(\alpha _{adj\,\, 1 })=\mu_2tan(\alpha _{adj\,\, 2 })\)
where,
\(\alpha_{adj\,\,1}=90^o+\alpha_1-\theta_1\)
and
\(\alpha_{adj\,\,2}=90^o+\alpha_2-\theta_2\)
as such,
\(\mu_1cot(\theta_1-\alpha_1)=\mu_2cot(\theta_2-\alpha_2)\)
\(\cfrac{tan(\theta_2-\alpha_2)}{tan(\theta_1-\alpha_1)}=\cfrac{\mu_2}{\mu_1}\)
But on the left side of the cone,
\(\alpha_{adj}=\theta-(90^o-\alpha)=\theta+\alpha-90^o\)
\(B_1sin(\alpha_{adj\,\,1})=B_2sin(\alpha_{adj\,\,2})\)
\(\cfrac{B_1}{\mu_1}cos(\alpha_{adj\,\,1})=\cfrac{B_2}{\mu_2}cos(\alpha_{adj\,\,2})\)
Dividing these two expressions,
\(\mu_1tan(\alpha_{adj\,\,1})=\mu_2tan(\alpha_{adj\,\,2})\)
Substitute for \(\alpha_{adj}\),
\(\mu_1tan(\theta_1+\alpha_1-90^o)=\mu_2tan(\theta_2+\alpha_2-90^o)\)
\(\mu_1cot(\theta_1+\alpha_1)=\mu_2cot(\theta_2+\alpha_2)\)
\(\cfrac{tan(\theta_2+\alpha_2)}{tan(\theta_1+\alpha_1)}=\cfrac{\mu_2}{\mu_1}\)
When \(\theta\) is smaller such that,
\(\alpha_{adj}=(90^o-\alpha)-\theta=90^o-(\theta+\alpha)\)
we obtain the same expression,
\(\mu_1tan(90^o-(\theta_1+\alpha_1))=\mu_2tan(90^o-(\theta_2+\alpha_2))\)
\(\mu_1cot(\theta_1+\alpha_1)=\mu_2cot(\theta_2+\alpha_2)\)
\(\cfrac{tan(\theta_2+\alpha_2)}{tan(\theta_1+\alpha_1)}=\cfrac{\mu_2}{\mu_1}\)
This means the ray will split into two, depending on which side of the cone the particle is on when it passes into the medium.
Banana!
since the base is perpendicular to the direction of incident, there is no need to adjust for \(\alpha\),
\(\cfrac { AB }{ v_{ 1 } } =\cfrac { A^{ ' }B^{ ' } }{ v_{ 2 } }\)
Since \(BA^{'}\) is common,
\(\cfrac {BA^{'} sin(\alpha _{1 }) }{ v_{ 1 } } =\cfrac {BA^{'} sin(\alpha _{ 2 }) }{ v_{ 2 } }\)
And
\(n.v=c\)
\(n\propto\cfrac{1}{v}\)
We have,
\(n_1sin(\alpha _{1 }) =n_2sin(\alpha _{ 2 }) \)
which is exactly Snell's Law. This is so, if the only factor resulting in refraction is the change in speed along the direction of incidence. We also have to consider how the \(B\) field behave at the interface.
When we consider the boundary conditions for the analogous \(B\) field on the right side of the cone, we have still,
\(B_1sin(\alpha_{adj\,\,1})=B_2sin(\alpha_{adj\,\,2})\)
\(\cfrac{B_1}{\mu_1}cos(\alpha_{adj\,\,1})=\cfrac{B_2}{\mu_2}cos(\alpha_{adj\,\,2})\)
\(\mu_1tan(\alpha _{adj\,\, 1 })=\mu_2tan(\alpha _{adj\,\, 2 })\)
where,
\(\alpha_{adj\,\,1}=90^o+\alpha_1-\theta_1\)
and
\(\alpha_{adj\,\,2}=90^o+\alpha_2-\theta_2\)
as such,
\(\mu_1cot(\theta_1-\alpha_1)=\mu_2cot(\theta_2-\alpha_2)\)
\(\cfrac{tan(\theta_2-\alpha_2)}{tan(\theta_1-\alpha_1)}=\cfrac{\mu_2}{\mu_1}\)
But on the left side of the cone,
\(\alpha_{adj}=\theta-(90^o-\alpha)=\theta+\alpha-90^o\)
\(B_1sin(\alpha_{adj\,\,1})=B_2sin(\alpha_{adj\,\,2})\)
\(\cfrac{B_1}{\mu_1}cos(\alpha_{adj\,\,1})=\cfrac{B_2}{\mu_2}cos(\alpha_{adj\,\,2})\)
Dividing these two expressions,
\(\mu_1tan(\alpha_{adj\,\,1})=\mu_2tan(\alpha_{adj\,\,2})\)
Substitute for \(\alpha_{adj}\),
\(\mu_1tan(\theta_1+\alpha_1-90^o)=\mu_2tan(\theta_2+\alpha_2-90^o)\)
\(\mu_1cot(\theta_1+\alpha_1)=\mu_2cot(\theta_2+\alpha_2)\)
When \(\theta\) is smaller such that,
\(\alpha_{adj}=(90^o-\alpha)-\theta=90^o-(\theta+\alpha)\)
we obtain the same expression,
\(\mu_1tan(90^o-(\theta_1+\alpha_1))=\mu_2tan(90^o-(\theta_2+\alpha_2))\)
\(\mu_1cot(\theta_1+\alpha_1)=\mu_2cot(\theta_2+\alpha_2)\)
\(\cfrac{tan(\theta_2+\alpha_2)}{tan(\theta_1+\alpha_1)}=\cfrac{\mu_2}{\mu_1}\)
This means the ray will split into two, depending on which side of the cone the particle is on when it passes into the medium.
Banana!
A Bloom Crosses Over
When a photon, modeled as a cone shaped spread of \(E\) field, is projected perpendicular from a medium of refractive index \(n_1\) into a medium of refractive index \(n_2\),
The \(E\) field being resolved into three components as shown, and applying the boundary conditions for an \(E\) field line,
\(E_{1\,3}=\cfrac{\varepsilon_2}{\varepsilon_1}E_{2\,3}\)
where the subscript \(3\) denotes the perpendicular direction, parallel to the surface normal.
\(E_{1}cos(\beta_1)=\cfrac{\varepsilon_2}{\varepsilon_1}E_{2}cos(\beta_2)\)
The tangential component remains the same,
\(E_1 sin(\beta_1)=E_2sin(\beta_2)\)
Dividing the two expressions above, we have,
\(\cfrac{ tan(\beta_2)}{tan(\beta_1)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
Since, \(\beta=90^o-\theta\)
\(tan(\beta)=tan(90^o-\theta)=cot(\theta)\)
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
When the dielectric constants,
\(\varepsilon_1\lt\varepsilon_2\)
The \(E\) field cone spreads and polarization \(\small{\theta}\) decreases. This is however, not dispersion.
When the photon is projected at an incline to the normal onto the interface \(\small{\varepsilon_1|\varepsilon_2}\),
The particle maintains its circular motion in both medium and the cone passes through the medium completely when its apex is on the interface, at the foot of the surface normal, we have,
\(\cfrac { AB }{ v_{ 1 } } =\cfrac { A^{ ' }B^{ ' } }{ v_{ 2 } } \)
Since \(BA^{'}\) is common,
\( \cfrac {BA^{'} sin(\alpha _{adj\,\, 1 }) }{ v_{ 1 } } =\cfrac {BA^{'} sin(\alpha _{adj\,\, 2 }) }{ v_{ 2 } } \)
where,
\(\alpha_{adj\,\,1}=90^o+\alpha_1-\theta_1\)
and
\(\alpha_{adj\,\,2}=90^o+\alpha_2-\theta_2\)
where \(\theta\) is polarization; the angle at which the circular path of the particle makes with the line of incidence.
Since,
\( n.v=c\)
\(\cfrac{1}{v}\propto n\)
and we have,
\( n_{ 1 }sin(\alpha _{adj\,\, 1 })=n_{ 2 }sin(\alpha _{ adj\,\,2 })\)
which is just Snell's Law with \(\alpha\) substituted by \(\alpha_{adj}\). Furthermore, this particle in circular motion that generates a \(E\) field is itself a \(B\) field. When we apply the boundary conditions appropriate for a \(B\) field upon the circulating particle at the point through the incident normal,
the normal components of \(B\) across the mediums are equal,
\(B_{ 1 }sin(\alpha _{ adj\,\,1 })=B_{ 2 }sin(\alpha _{ adj\,\,2 })\)
where,
\(\alpha_{adj\,\,1}=90^o+\alpha_1-\theta_1\)
and
\(\alpha_{adj\,\,2}=90^o+\alpha_2-\theta_2\)
where \(\theta\) is polarization; the angle at which the circular path of the particle makes with the line of incidence.
\( \cfrac { B_{ 1 } }{ B_{ 2 } } =\cfrac { sin(\alpha _{ adj\,\,2 }) }{ sin(\alpha _{ adj\,\,1 }) } \)
and the tangential component of \(H=\cfrac{B}{\mu}\) across the medium are equal,
\(\cfrac { B_{ 1 }cos(\alpha _{adj\,\, 1 }) }{ \mu _{ 1 } } =\cfrac { B_{ 2 }cos(\alpha _{adj\,\, 2 }) }{ \mu _{ 2 } } \)
So,
\( \cfrac { sin(\alpha _{ adj\,\,2 }) }{ sin(\alpha _{ adj\,\,1 }) } =\cfrac { \mu _{ 1 } }{ \mu _{ 2 } } \cfrac { cos(\alpha _{ adj\,\,2 }) }{ cos(\alpha _{ adj\,\,1 }) } \)
\( \cfrac { tan(\alpha _{ adj\,\,2 }) }{ tan(\alpha _{adj\,\, 1 }) } =\cfrac { \mu _{ 1 } }{ \mu _{ 2 } } \)
\(\mu_1tan(\alpha _{adj\,\, 1 })=\mu_2tan(\alpha _{adj\,\, 2 })\) ---(*)
Snell's law is due to the change in velocity along the ray with the particle still in circular motion in the perpendicular direction, at \(AA^{'}\) and \(BB^{'}\). The last expression (*) is the result of applying boundary conditions on the analogous \(B\) field. Applying boundary conditions to the \(E\) field indicates a change in polarization \(\theta\) as the photon crosses the interface \(\small{\varepsilon_1|\varepsilon_2}\).
In the case of an EMW, the \(E\) field is reversed, but all expressions developed above are still true.
The \(E\) field being resolved into three components as shown, and applying the boundary conditions for an \(E\) field line,
\(E_{1\,3}=\cfrac{\varepsilon_2}{\varepsilon_1}E_{2\,3}\)
where the subscript \(3\) denotes the perpendicular direction, parallel to the surface normal.
\(E_{1}cos(\beta_1)=\cfrac{\varepsilon_2}{\varepsilon_1}E_{2}cos(\beta_2)\)
The tangential component remains the same,
\(E_1 sin(\beta_1)=E_2sin(\beta_2)\)
Dividing the two expressions above, we have,
\(\cfrac{ tan(\beta_2)}{tan(\beta_1)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
Since, \(\beta=90^o-\theta\)
\(tan(\beta)=tan(90^o-\theta)=cot(\theta)\)
\(\cfrac{ tan(\theta_1)}{tan(\theta_2)}=\cfrac{\varepsilon_2}{\varepsilon_1}\)
When the dielectric constants,
\(\varepsilon_1\lt\varepsilon_2\)
The \(E\) field cone spreads and polarization \(\small{\theta}\) decreases. This is however, not dispersion.
When the photon is projected at an incline to the normal onto the interface \(\small{\varepsilon_1|\varepsilon_2}\),
The particle maintains its circular motion in both medium and the cone passes through the medium completely when its apex is on the interface, at the foot of the surface normal, we have,
\(\cfrac { AB }{ v_{ 1 } } =\cfrac { A^{ ' }B^{ ' } }{ v_{ 2 } } \)
Since \(BA^{'}\) is common,
\( \cfrac {BA^{'} sin(\alpha _{adj\,\, 1 }) }{ v_{ 1 } } =\cfrac {BA^{'} sin(\alpha _{adj\,\, 2 }) }{ v_{ 2 } } \)
where,
\(\alpha_{adj\,\,1}=90^o+\alpha_1-\theta_1\)
and
\(\alpha_{adj\,\,2}=90^o+\alpha_2-\theta_2\)
where \(\theta\) is polarization; the angle at which the circular path of the particle makes with the line of incidence.
Since,
\( n.v=c\)
\(\cfrac{1}{v}\propto n\)
and we have,
\( n_{ 1 }sin(\alpha _{adj\,\, 1 })=n_{ 2 }sin(\alpha _{ adj\,\,2 })\)
which is just Snell's Law with \(\alpha\) substituted by \(\alpha_{adj}\). Furthermore, this particle in circular motion that generates a \(E\) field is itself a \(B\) field. When we apply the boundary conditions appropriate for a \(B\) field upon the circulating particle at the point through the incident normal,
the normal components of \(B\) across the mediums are equal,
\(B_{ 1 }sin(\alpha _{ adj\,\,1 })=B_{ 2 }sin(\alpha _{ adj\,\,2 })\)
where,
\(\alpha_{adj\,\,1}=90^o+\alpha_1-\theta_1\)
and
\(\alpha_{adj\,\,2}=90^o+\alpha_2-\theta_2\)
where \(\theta\) is polarization; the angle at which the circular path of the particle makes with the line of incidence.
\( \cfrac { B_{ 1 } }{ B_{ 2 } } =\cfrac { sin(\alpha _{ adj\,\,2 }) }{ sin(\alpha _{ adj\,\,1 }) } \)
and the tangential component of \(H=\cfrac{B}{\mu}\) across the medium are equal,
\(\cfrac { B_{ 1 }cos(\alpha _{adj\,\, 1 }) }{ \mu _{ 1 } } =\cfrac { B_{ 2 }cos(\alpha _{adj\,\, 2 }) }{ \mu _{ 2 } } \)
So,
\( \cfrac { sin(\alpha _{ adj\,\,2 }) }{ sin(\alpha _{ adj\,\,1 }) } =\cfrac { \mu _{ 1 } }{ \mu _{ 2 } } \cfrac { cos(\alpha _{ adj\,\,2 }) }{ cos(\alpha _{ adj\,\,1 }) } \)
\( \cfrac { tan(\alpha _{ adj\,\,2 }) }{ tan(\alpha _{adj\,\, 1 }) } =\cfrac { \mu _{ 1 } }{ \mu _{ 2 } } \)
\(\mu_1tan(\alpha _{adj\,\, 1 })=\mu_2tan(\alpha _{adj\,\, 2 })\) ---(*)
Snell's law is due to the change in velocity along the ray with the particle still in circular motion in the perpendicular direction, at \(AA^{'}\) and \(BB^{'}\). The last expression (*) is the result of applying boundary conditions on the analogous \(B\) field. Applying boundary conditions to the \(E\) field indicates a change in polarization \(\theta\) as the photon crosses the interface \(\small{\varepsilon_1|\varepsilon_2}\).
In the case of an EMW, the \(E\) field is reversed, but all expressions developed above are still true.
Sunday, August 9, 2015
Dispersion of EMW And Photons
In both EMW and photon, dispersion results from \(\small{\theta\lt90^o}\), due to the non zero vertical component of \(E\).
When \(\small{\theta=90^o}\) there is no dispersion.
When \(\small{\theta=90^o}\) there is no dispersion.
Counter Force Components?
Continued from the previous post "Cosmetics Attracting Attentions" dated 08 Aug 2015,
Still, the physical significance of these angles are not obvious on paper.
Is this in total,
\(\cfrac{3\pi}{4}+\cfrac{\pi}{4}=\pi\)
a \(\small{180^o}\) phase difference between \(F_\rho\) and \(x\) when \(F_\rho\) is sinusoidal.
Still, the physical significance of these angles are not obvious on paper.
Is this in total,
\(\cfrac{3\pi}{4}+\cfrac{\pi}{4}=\pi\)
a \(\small{180^o}\) phase difference between \(F_\rho\) and \(x\) when \(F_\rho\) is sinusoidal.
Cosmetics Attracting Attentions
From the post ""the post "Not Exponential, But Hyperbolic And Positive Gravity!" dated 22 Nov 2014,
\(F_{\rho}=e^{ i3\pi /4 }D\sqrt { 2{ mc^{ 2 } } } .tanh\left( \cfrac { { D } }{ \sqrt { 2{ mc^{ 2 } } } }( x-x_o).e^{ i\pi /4 } \right)\)
where we insist that,
\(G=D.e^{ i\pi /4 }\)
is real,
But given,
\(tanh(x)=\cfrac{e^x-e^{-x}}{e^x+e^{-x}}=\cfrac{1-e^{-2x}}{1+e^{-2x}}\)
D can be real.
Consider,
\(e^{ i\pi /4 }=(e^{ i\pi /2 })^{1/2}=\sqrt{i}\)
that follows from Euler's
\(e^{i\pi}+1=0\)
An so,
\(tanh(h\sqrt{i})=\cfrac{1-e^{-2h\sqrt{i}}}{1+e^{-2h\sqrt{i}}}\)
where
\(h=\cfrac { { D } }{ \sqrt { 2{ mc^{ 2 } } } }( x-x_o)\)
and
\(e^{ i3\pi /4 }=i^{3/2}=i\sqrt{i}\)
\(F_{\rho}=i\sqrt{i}.D\sqrt { 2{ mc^{ 2 } } } .\cfrac{1-e^{-2h\sqrt{i}}}{1+e^{-2h\sqrt{i}}}\)
and if we define,
\(\varphi=\sqrt{i}\)
\(F_{\rho}=\varphi^3.D\sqrt { 2{ mc^{ 2 } } } .\cfrac{1-e^{-2\varphi h}}{1+e^{-2\varphi h}}\)
where
\(\varphi\) rotates \(45^o\) and \(\varphi^3\) rotates \(135^o\) from the direction of \(x\).
Cosmetics to bring attention to the these two rotations; they have significance, but what?
Furthermore,
\(\sqrt{2mc^2}=\sqrt{m(\sqrt{2}c)^2}\)
also has significance; it implies that across two orthogonal dimensions, in place of \(c\) is \(\sqrt{2}c\). This suggests that if entanglement is the reason for light speed limit, then entanglement is dimension specific, a different type of entanglement occurs along each orthogonal dimension; a different entanglement of the specific energy defining that dimension. Particles can be limited separately along \(t_c\) where in entanglement with other particles share electrostatic energy, and at the same time limited along \(t_g\) where they share gravitational energy; ditto for \(t_T\).
Since we normally dealt with energy of a particular sort, \(\sqrt{2}c\) has never arise until we cross between orthogonal dimensions.
In space,
\(c^2+c^2=2c^2\)
\(2c^2+c^2=3c^2\)
And the speed limit we encountered first was,
\(c=\sqrt{3}k\)
where \(k\) is a constant, \(c\) light speed. Three groups of particles entangled separately across three space dimensions with the one particle under observation.
Note: \(\small{\sqrt{3}=1.7320508075688773...}\) is not rational. Looking for more significant numbers to \(c\) may just be chasing after the tail of \(\small{\sqrt{3}}\).
\(F_{\rho}=e^{ i3\pi /4 }D\sqrt { 2{ mc^{ 2 } } } .tanh\left( \cfrac { { D } }{ \sqrt { 2{ mc^{ 2 } } } }( x-x_o).e^{ i\pi /4 } \right)\)
where we insist that,
\(G=D.e^{ i\pi /4 }\)
is real,
But given,
\(tanh(x)=\cfrac{e^x-e^{-x}}{e^x+e^{-x}}=\cfrac{1-e^{-2x}}{1+e^{-2x}}\)
D can be real.
Consider,
\(e^{ i\pi /4 }=(e^{ i\pi /2 })^{1/2}=\sqrt{i}\)
that follows from Euler's
\(e^{i\pi}+1=0\)
An so,
\(tanh(h\sqrt{i})=\cfrac{1-e^{-2h\sqrt{i}}}{1+e^{-2h\sqrt{i}}}\)
where
\(h=\cfrac { { D } }{ \sqrt { 2{ mc^{ 2 } } } }( x-x_o)\)
and
\(e^{ i3\pi /4 }=i^{3/2}=i\sqrt{i}\)
\(F_{\rho}=i\sqrt{i}.D\sqrt { 2{ mc^{ 2 } } } .\cfrac{1-e^{-2h\sqrt{i}}}{1+e^{-2h\sqrt{i}}}\)
and if we define,
\(\varphi=\sqrt{i}\)
\(F_{\rho}=\varphi^3.D\sqrt { 2{ mc^{ 2 } } } .\cfrac{1-e^{-2\varphi h}}{1+e^{-2\varphi h}}\)
where
\(\varphi\) rotates \(45^o\) and \(\varphi^3\) rotates \(135^o\) from the direction of \(x\).
Cosmetics to bring attention to the these two rotations; they have significance, but what?
Furthermore,
\(\sqrt{2mc^2}=\sqrt{m(\sqrt{2}c)^2}\)
also has significance; it implies that across two orthogonal dimensions, in place of \(c\) is \(\sqrt{2}c\). This suggests that if entanglement is the reason for light speed limit, then entanglement is dimension specific, a different type of entanglement occurs along each orthogonal dimension; a different entanglement of the specific energy defining that dimension. Particles can be limited separately along \(t_c\) where in entanglement with other particles share electrostatic energy, and at the same time limited along \(t_g\) where they share gravitational energy; ditto for \(t_T\).
Since we normally dealt with energy of a particular sort, \(\sqrt{2}c\) has never arise until we cross between orthogonal dimensions.
In space,
\(c^2+c^2=2c^2\)
\(2c^2+c^2=3c^2\)
And the speed limit we encountered first was,
\(c=\sqrt{3}k\)
where \(k\) is a constant, \(c\) light speed. Three groups of particles entangled separately across three space dimensions with the one particle under observation.
Note: \(\small{\sqrt{3}=1.7320508075688773...}\) is not rational. Looking for more significant numbers to \(c\) may just be chasing after the tail of \(\small{\sqrt{3}}\).
Asymmetry Lost
From the post "High Frequency EMW From Laser" dated 31 Jul 2015 and "It's All Fluorescence Outside, Inside" dated 29 Jul 2015, the cone provides the asymmetry that differentiate between a counter clockwise rotating particle generating a \(E\) field outwards and a clockwise rotating particle generating a \(E\) field inwards. This asymmetry is lost when \(\small{\theta\to90^o}\),
Both clockwise and anti-clockwise rotations generate a \(E\) field parallel to \(PO\). This radiation is distinct from EMW and photons. Neither,
\(B=i\cfrac{\partial\,E}{\partial x}\)
nor
\(B=-i\cfrac{\partial\,E}{\partial x}\)
is applicable. And occurs in a single burst as \(\small{v_{cir}\approx0}\) is swapped as \(\small{v_{shm}}\) on emission and the particle stopped oscillating, from the post "It's All Fluorescence Outside, Inside" dated 29 Jul 2015.
This is a short burst of \(E\) field towards \(O\).
Both clockwise and anti-clockwise rotations generate a \(E\) field parallel to \(PO\). This radiation is distinct from EMW and photons. Neither,
\(B=i\cfrac{\partial\,E}{\partial x}\)
nor
\(B=-i\cfrac{\partial\,E}{\partial x}\)
is applicable. And occurs in a single burst as \(\small{v_{cir}\approx0}\) is swapped as \(\small{v_{shm}}\) on emission and the particle stopped oscillating, from the post "It's All Fluorescence Outside, Inside" dated 29 Jul 2015.
This is a short burst of \(E\) field towards \(O\).
Clouds part and blend
and the rain
rattles its way
she calls for love
but in the thunderous
silence
Blushing cheeks
a bloom among beauties
she stood
her hands aside
she gave love
received none
Clouds descend and
in gentle embrace
love all
love quiet
Such love upon us
everyday
What's there to be?
A choke hold's
not love
"I am sorry?.." ???
Love in command
of a upper hand?...
The sun breaks
and nature breathes
a new day
love of freshness
drives the stills away
Such love upon us
everyday
A blossom sings
tears on her petals
sway
in songs of love and sorrows
The thinning mist
in gentle drifts
love all
love quiet
Let your heart rest
and heal
It is morning...
always
words to a tune
as memories mend
《Quiet Love》
and the rain
rattles its way
she calls for love
but in the thunderous
silence
Blushing cheeks
a bloom among beauties
she stood
her hands aside
she gave love
received none
Clouds descend and
in gentle embrace
love all
love quiet
Such love upon us
everyday
What's there to be?
A choke hold's
not love
"I am sorry?.." ???
Love in command
of a upper hand?...
The sun breaks
and nature breathes
a new day
love of freshness
drives the stills away
Such love upon us
everyday
A blossom sings
tears on her petals
sway
in songs of love and sorrows
The thinning mist
in gentle drifts
love all
love quiet
Let your heart rest
and heal
It is morning...
always
words to a tune
as memories mend
《Quiet Love》
Saturday, August 8, 2015
More Squeeze Rhythmically
From he post "\(\psi_{max}\) Is New And Important" dated 13 Jul 2015,
\(F=\psi_{n}-\psi(x)=m\cfrac{d^2x}{dt^2}\)
when we substitute for \(\psi(x)\),
\(\psi(x)=-i{ 2{ mc^{ 2 } } }\,ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } }(x-x_z)))+c\) --- (*)
from the post "Not Quite The Same Newtonian Field" dated 23 Nov 2015. Assuming that at \(x=0\), \(\psi(0)=0\),
\(c=i{ 2{ mc^{ 2 } } }\,ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } }(x_z)))\)
and so,
\(\psi(x_z)=\psi_{max}=i{ 2{ mc^{ 2 } } }\,ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } }(x_z)))\)
Therefore,
\(m\cfrac { d^{ 2 }x }{ dt^{ 2 } } =\psi _{ n }+i2{ mc^{ 2 } }ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } (x-x_z)))-\psi_{max}\)
\(m\cfrac { d^{ 2 }x }{ dt^{ 2 } } =i2{ mc^{ 2 } }ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } (x-x_z)))+\psi_{c}\)
where
\(\psi_c=\psi_n-\psi_{max}\)
In cases where,
\(\psi_d=\psi_{max}-\psi_n\)
we have a particle of opposite sign embedded in another particle.
Also,
\(\psi_n=\psi _{ photon }+\psi_{o}\)
\(\psi_n\) is the elevated energy level of the particle from its ground state \(\psi_{o}\) after receiving the photon \(\psi _{ photon }\).
In the case when,
\(\psi _{ photon }=0\), \(\psi_c=\psi_o-\psi_{max}\)
and \(\psi_c\) is a constant. Since,
\(F=m\cfrac { d^{ 2 }x }{ dt^{ 2 } } \)
\(F=i2{ mc^{ 2 } }ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } (x-x_z)))+\psi_{c}\)
We now consider the effect of exerting an external force on the system, the resulting change in \(x\), the relative displacement of the embedded particle and the containing particle can be obtained from the expression,
\(\cfrac{dF}{dx}=iG \sqrt { 2{ mc^{ 2 } } }.tanh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } (x-x_z))\)
\(F=\psi_{n}-\psi(x)=m\cfrac{d^2x}{dt^2}\)
when we substitute for \(\psi(x)\),
\(\psi(x)=-i{ 2{ mc^{ 2 } } }\,ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } }(x-x_z)))+c\) --- (*)
from the post "Not Quite The Same Newtonian Field" dated 23 Nov 2015. Assuming that at \(x=0\), \(\psi(0)=0\),
\(c=i{ 2{ mc^{ 2 } } }\,ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } }(x_z)))\)
and so,
\(\psi(x_z)=\psi_{max}=i{ 2{ mc^{ 2 } } }\,ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } }(x_z)))\)
Therefore,
\(m\cfrac { d^{ 2 }x }{ dt^{ 2 } } =\psi _{ n }+i2{ mc^{ 2 } }ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } (x-x_z)))-\psi_{max}\)
\(m\cfrac { d^{ 2 }x }{ dt^{ 2 } } =i2{ mc^{ 2 } }ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } (x-x_z)))+\psi_{c}\)
where
\(\psi_c=\psi_n-\psi_{max}\)
In cases where,
\(\psi_d=\psi_{max}-\psi_n\)
we have a particle of opposite sign embedded in another particle.
Also,
\(\psi_n=\psi _{ photon }+\psi_{o}\)
\(\psi_n\) is the elevated energy level of the particle from its ground state \(\psi_{o}\) after receiving the photon \(\psi _{ photon }\).
In the case when,
\(\psi _{ photon }=0\), \(\psi_c=\psi_o-\psi_{max}\)
and \(\psi_c\) is a constant. Since,
\(F=m\cfrac { d^{ 2 }x }{ dt^{ 2 } } \)
\(F=i2{ mc^{ 2 } }ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } (x-x_z)))+\psi_{c}\)
We now consider the effect of exerting an external force on the system, the resulting change in \(x\), the relative displacement of the embedded particle and the containing particle can be obtained from the expression,
\(\cfrac{dF}{dx}=iG \sqrt { 2{ mc^{ 2 } } }.tanh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } (x-x_z))\)
which is just the force density expression we formulated in the post "Not Exponential, But Hyperbolic And Positive Gravity!" dated 22 Nov 2014. More explicitly,
\(F_{\rho}=e^{ i3\pi /4 }D\sqrt { 2{ mc^{ 2 } } } .tanh\left( \cfrac { { D } }{ \sqrt { 2{ mc^{ 2 } } } }( x-x_o).e^{ i\pi /4 } \right)\)
where we insist that,
\(G=D.e^{ i\pi /4 }\)
is real.
The term \(i\) originates from the expression for \(\psi\), which is a wave in the \(ix\) direction. From the post "Opps Lucky Me" dated 25 May 2015, the Newtonian force \(F_{\small{N}}\)
\(F_{\small{N}}=-\psi\)
and the post "From The Very Big To The Very Small" dated 16 Jul 2015.
\(F_{x}=\int_0^x{F_{\rho}}dx\)
so,
\(F_{\small{N}}=\int{F_{\rho}}dx\)
where \(x=0\) when \(F_{\small{N}}=0\). Combining all these, the Newtonian force \(F_{\small{N}}\) when applied resulting in a deformation \(\Delta x\) is given by,
\(F_{\small{N}}=\cfrac{dF}{dx}|_{x=x_o}.\Delta x=i2{ mc^{ 2 } }ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } (x-x_z)))|_{x=x_o}.\Delta x\) --- (*)
where \(F_{\small{N}}\) can be the result of an applied electric field, \(E\) or magnetic field \(B\).
When \(\Delta x\) changes \(\theta\) around \(\theta=45^o\), an EMW together with an photon are emitted. The EMW can be amplified and be used as the driving force (positive feedback) and thus generates sustained oscillations.
And we have a problem with \(i\) on the RHS of the expression for \(F_{\small{N}}\), otherwise we have an indication for electrostriction/magnetostriction and piezoelectric.
The problem is \(i\) does make sense,
where the deformation, \(\Delta x\) is in the direction perpendicular to \(F_{\small{N}}\). This is the result of \(\psi\) being perpendicular to the direction of \(x\), from the expression (*). Since the total volume of the material (\(\psi\)), is approximately a constant, there are corresponding deformations in the two perpendicular directions with respect to \(\Delta x\) too.
With the issue of \(i\) aside,
we differentiate between piezoelectricity and its linear dependence on the applied force \(F_{\small{N}}\), and electrostriction and its quadratic dependence on the applied force, base on the same expression (*). Piezoelectricity requires that \(\small{\Delta x}\) changes \(\small{\theta}\) around \(\small{\theta=45^o}\).
where the deformation, \(\Delta x\) is in the direction perpendicular to \(F_{\small{N}}\). This is the result of \(\psi\) being perpendicular to the direction of \(x\), from the expression (*). Since the total volume of the material (\(\psi\)), is approximately a constant, there are corresponding deformations in the two perpendicular directions with respect to \(\Delta x\) too.
With the issue of \(i\) aside,
we differentiate between piezoelectricity and its linear dependence on the applied force \(F_{\small{N}}\), and electrostriction and its quadratic dependence on the applied force, base on the same expression (*). Piezoelectricity requires that \(\small{\Delta x}\) changes \(\small{\theta}\) around \(\small{\theta=45^o}\).
Friday, August 7, 2015
Sign Issue, Side Issue
\(sin(\theta)\) is still positive on the other side of the center \(O\). \(\theta\) is always positive, when measured consistently.
From this reason, both \(\small{v_{cir}}\) and \(\small{v_{shm}}\) are negative at the same time. Where, from the post "Twirl Plus SHM, Spinning Coin" dated 17 Jul 2015,
\(v^{ 2 }_{ cir }=cos(\theta )(x+x_{ z })\left\{ -2{ c^{ 2 } }cos(\theta )ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } x))+\cfrac { \psi _{ d } }{ m } \right\}\)
and
\(v^{ 2 }_{ shm }=sin(\theta )(x+x_{ z })\left\{ -2{ c^{ 2 } }cos(\theta )ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } x))+\cfrac { \psi _{ d } }{ m } \right\}\)
their signs depend on the common term,
\((x+x_{ z })\left\{ -2{ c^{ 2 } }cos(\theta )ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } x))+\cfrac { \psi _{ d } }{ m } \right\}\)
When
\(v_{cir}=v_{shm}=c\)
\(x_d=x_v\)
circular motion is in a plane whose normal at the center of the circular path passes above \(O\), the center of oscillation. This occurs instantaneously and does not alter the analysis presented.
Have a nice day.
From this reason, both \(\small{v_{cir}}\) and \(\small{v_{shm}}\) are negative at the same time. Where, from the post "Twirl Plus SHM, Spinning Coin" dated 17 Jul 2015,
\(v^{ 2 }_{ cir }=cos(\theta )(x+x_{ z })\left\{ -2{ c^{ 2 } }cos(\theta )ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } x))+\cfrac { \psi _{ d } }{ m } \right\}\)
and
\(v^{ 2 }_{ shm }=sin(\theta )(x+x_{ z })\left\{ -2{ c^{ 2 } }cos(\theta )ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } x))+\cfrac { \psi _{ d } }{ m } \right\}\)
their signs depend on the common term,
\((x+x_{ z })\left\{ -2{ c^{ 2 } }cos(\theta )ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } x))+\cfrac { \psi _{ d } }{ m } \right\}\)
When
\(v_{cir}=v_{shm}=c\)
\(x_d=x_v\)
circular motion is in a plane whose normal at the center of the circular path passes above \(O\), the center of oscillation. This occurs instantaneously and does not alter the analysis presented.
Have a nice day.
Two For TwoTwo
Continued from the previous post "Spread Beyond Light Speed" dated 07 Aug 2015,
For a oscillating system the maximum speed at the center is,
\(v_{max}=\omega.A\)
where \(A\) is the amplitude of oscillation, and \(\omega\) the angular frequency.
Either \(\omega\) or \(A\) can vary to accommodate the change in \(v_{max}\).
But neither happens util the end of the oscillation at \(x=A\), where the particle returns towards the center of the \(\psi\) cloud.
The change in circular motion frequency occurs instantaneously at the center, when the circular velocity is swapped. The frequency change, \(\small{\Delta f}\),
\(\Delta f=\cfrac{v_{cir}}{2\pi x_c}-\cfrac{v_{shm}}{2\pi x_c}=\cfrac{1}{2\pi x_c}(v_{cir}-v_{shm})\)
and the energy change \(\small{\Delta E}\),
\(\Delta E=\cfrac{1}{2}m({v^2_{cir}}-{v^2_{shm}})=\cfrac{1}{2}m(v_{cir}+v_{shm})(v_{cir}-v_{shm})\)
\(\Delta E=m{\pi x_c}(v_{cir}+v_{shm})\Delta f\)
Since \(v_{cir}\) and \(v_{shm}\) are both driven to light speed at \(x=A\) (at the beginning),
\(v_{shm}=c\) and \(v_{cir}=c\)
(these were the values we started with when the particle in circular motion at light speed, absorbs a photon and is driven to \(x_d=A\) from the center at light speed. The \(v^2\) vs \(x\) graph was used twice, once to find the radius of circular motion and then again to find the position of the particle (from the center of \(\psi\)), when it has light speed in a direction always perpendicular to the circular velocity.)
\(\Delta E={2\pi x_c}mc.\Delta f\)
From the posts "de Broglie Per Unit Volume" and "de Broglie Per Person" both dated 20 Dec 2014, where Planck's constant is,
\(h=2\pi a_{ \psi }mc\)
We obtain,
\(\Delta E=h\Delta f\)
which is Planck's relation if \(x_c=a_\psi\).
This means, the particle's motion extends to the edge of the \(\psi\) cloud at the radius \(a_\psi\). Light speed is the first constraint on the particle's motion, the extend of \(\psi\), \(a_\psi\) serves as the second constraint on the particle's motion when it is bombarded with photons.
Two constraints for two superimposed "linear" motions.
Note: If \(v_{shm}=c\) and \(v_{cir}=c\) then why is \((v_{cir}-v_{shm})\) not immediately zero? The answer is in the difference between instantaneous values and time averaged values. In an oscillatory system you would pick the point at which energy is maximum to be the total energy of the system. In this case, \(\small{\Delta f}\) is calculated from \(\small{(v_{cir}-v_{shm})}\) and the latter is substituted away. And energy change is calculated with \(x_c=A\), at the beginning of the particle's superimposed motion. In other words, energy change with reference to the energy of the system at \(x_c=A\), in the beginning.
For a oscillating system the maximum speed at the center is,
\(v_{max}=\omega.A\)
where \(A\) is the amplitude of oscillation, and \(\omega\) the angular frequency.
Either \(\omega\) or \(A\) can vary to accommodate the change in \(v_{max}\).
But neither happens util the end of the oscillation at \(x=A\), where the particle returns towards the center of the \(\psi\) cloud.
The change in circular motion frequency occurs instantaneously at the center, when the circular velocity is swapped. The frequency change, \(\small{\Delta f}\),
\(\Delta f=\cfrac{v_{cir}}{2\pi x_c}-\cfrac{v_{shm}}{2\pi x_c}=\cfrac{1}{2\pi x_c}(v_{cir}-v_{shm})\)
and the energy change \(\small{\Delta E}\),
\(\Delta E=\cfrac{1}{2}m({v^2_{cir}}-{v^2_{shm}})=\cfrac{1}{2}m(v_{cir}+v_{shm})(v_{cir}-v_{shm})\)
\(\Delta E=m{\pi x_c}(v_{cir}+v_{shm})\Delta f\)
Since \(v_{cir}\) and \(v_{shm}\) are both driven to light speed at \(x=A\) (at the beginning),
\(v_{shm}=c\) and \(v_{cir}=c\)
(these were the values we started with when the particle in circular motion at light speed, absorbs a photon and is driven to \(x_d=A\) from the center at light speed. The \(v^2\) vs \(x\) graph was used twice, once to find the radius of circular motion and then again to find the position of the particle (from the center of \(\psi\)), when it has light speed in a direction always perpendicular to the circular velocity.)
\(\Delta E={2\pi x_c}mc.\Delta f\)
From the posts "de Broglie Per Unit Volume" and "de Broglie Per Person" both dated 20 Dec 2014, where Planck's constant is,
\(h=2\pi a_{ \psi }mc\)
We obtain,
\(\Delta E=h\Delta f\)
which is Planck's relation if \(x_c=a_\psi\).
This means, the particle's motion extends to the edge of the \(\psi\) cloud at the radius \(a_\psi\). Light speed is the first constraint on the particle's motion, the extend of \(\psi\), \(a_\psi\) serves as the second constraint on the particle's motion when it is bombarded with photons.
Two constraints for two superimposed "linear" motions.
Note: If \(v_{shm}=c\) and \(v_{cir}=c\) then why is \((v_{cir}-v_{shm})\) not immediately zero? The answer is in the difference between instantaneous values and time averaged values. In an oscillatory system you would pick the point at which energy is maximum to be the total energy of the system. In this case, \(\small{\Delta f}\) is calculated from \(\small{(v_{cir}-v_{shm})}\) and the latter is substituted away. And energy change is calculated with \(x_c=A\), at the beginning of the particle's superimposed motion. In other words, energy change with reference to the energy of the system at \(x_c=A\), in the beginning.
Spread Beyond Light Speed
From the graphs of emission and absorption of a fluorescence material, the right tail of the absorption graph is similar to the left arm of the emission spectrum.
The graphs were taken from the site: http://www.iss.com/resources/research/technical_notes/PC1_LWPolarizationStandards.html
This give rise to the relation at the cross point,
\(f_{cross}=f_{max}+\cfrac{1}{2}\Delta f\)
where \(f_{max}\) is the preceding maximum point, \(\Delta f\) is the difference between the two peaks and \(f_{cross}\) at the cross point.
On the absorption graph the right arm plots the the energy of the absorbed photons that bring the energy of the particle beyond \(\small{\cfrac{1}{2}mc^2}\). On the emission graph both arms graph the spread of energy around \(\small{\cfrac{1}{2}mc^2}\). The theoretical emission graph is given in the post '"Not Exactly A Fluorescence Polarizer" dated 28 Jul 2015. Both the right arm of the absorption spectrum and the left arm of the emission spectrum graph the spread of energy where the particle is at/around light speed \(c\).
The similarity between the two graphs suggest that the underlying mechanism that store energy when the particle is at light speed are of similar nature. This energy beyond the particle's \(\small{KE=\cfrac{1}{2}mc^2}\), is wholly emitted. We see this from the emission graphs that begin immediately after the local maxima on the absorption graph. At the absorption maxima, the particle is at light speed.
This suggests that the particle is first driven to light speed through photons absorption and then it oscillates about the \(\psi\) cloud center. Photons emission occurs at the center.
What happens when the particle swaps velocities \(\small{v_{cir}\to v_{shm}}\), \(\small{v_{shm}\to v_{cir}}\) as the post "Color!" dated 25 Jul 2015 suggests?
Mathematically this swap occurs with certainty. At the center both \(\small{v^2_{cir}}\) and \(\small{v^2_{shm}}\) attains a negative sign, and so both \(\small{v_{cir}}\) and \(\small{v_{shm}}\) are multiplied by a factor \(i\). This changes \(\small{v_{cir}}\) to be along \(x\), the radial line and \(\small{v_{shm}}\) to be perpendicular to \(x\). The particle now oscillates with velocity \(\small{v_{cir}}\) and performs circular motion with velocity \(\small{v_{shm}}\). The change in circular motion frequency results in the emission or absorption of a photon. (Paradoxically, both \(\small{v^2_{cir}}\) and \(\small{v^2_{shm}}\) are zero, at the center, after that they are both negative.)
Does the change in oscillation frequency also result in an emission/absorption of a quantum of energy? This question arises because the projection of circular motion onto the diameter of its circular path is SHM oscillation. Oscillations can be viewed as projected circular motion along the diameter.
The particle's motion is the superposition of circular motion and oscillation. One energy packet is enough to account for energy gain or loss from its resultant motion. But where did this packet of energy originate from? Circular motion or oscillation? The initial delay when the particle first absorbs a photon then emits one for values of \(\small{\theta\gt45^o}\) suggests that the packet of energy is from circular motion.
The graphs were taken from the site: http://www.iss.com/resources/research/technical_notes/PC1_LWPolarizationStandards.html
This give rise to the relation at the cross point,
\(f_{cross}=f_{max}+\cfrac{1}{2}\Delta f\)
where \(f_{max}\) is the preceding maximum point, \(\Delta f\) is the difference between the two peaks and \(f_{cross}\) at the cross point.
On the absorption graph the right arm plots the the energy of the absorbed photons that bring the energy of the particle beyond \(\small{\cfrac{1}{2}mc^2}\). On the emission graph both arms graph the spread of energy around \(\small{\cfrac{1}{2}mc^2}\). The theoretical emission graph is given in the post '"Not Exactly A Fluorescence Polarizer" dated 28 Jul 2015. Both the right arm of the absorption spectrum and the left arm of the emission spectrum graph the spread of energy where the particle is at/around light speed \(c\).
The similarity between the two graphs suggest that the underlying mechanism that store energy when the particle is at light speed are of similar nature. This energy beyond the particle's \(\small{KE=\cfrac{1}{2}mc^2}\), is wholly emitted. We see this from the emission graphs that begin immediately after the local maxima on the absorption graph. At the absorption maxima, the particle is at light speed.
This suggests that the particle is first driven to light speed through photons absorption and then it oscillates about the \(\psi\) cloud center. Photons emission occurs at the center.
What happens when the particle swaps velocities \(\small{v_{cir}\to v_{shm}}\), \(\small{v_{shm}\to v_{cir}}\) as the post "Color!" dated 25 Jul 2015 suggests?
Mathematically this swap occurs with certainty. At the center both \(\small{v^2_{cir}}\) and \(\small{v^2_{shm}}\) attains a negative sign, and so both \(\small{v_{cir}}\) and \(\small{v_{shm}}\) are multiplied by a factor \(i\). This changes \(\small{v_{cir}}\) to be along \(x\), the radial line and \(\small{v_{shm}}\) to be perpendicular to \(x\). The particle now oscillates with velocity \(\small{v_{cir}}\) and performs circular motion with velocity \(\small{v_{shm}}\). The change in circular motion frequency results in the emission or absorption of a photon. (Paradoxically, both \(\small{v^2_{cir}}\) and \(\small{v^2_{shm}}\) are zero, at the center, after that they are both negative.)
Does the change in oscillation frequency also result in an emission/absorption of a quantum of energy? This question arises because the projection of circular motion onto the diameter of its circular path is SHM oscillation. Oscillations can be viewed as projected circular motion along the diameter.
The particle's motion is the superposition of circular motion and oscillation. One energy packet is enough to account for energy gain or loss from its resultant motion. But where did this packet of energy originate from? Circular motion or oscillation? The initial delay when the particle first absorbs a photon then emits one for values of \(\small{\theta\gt45^o}\) suggests that the packet of energy is from circular motion.
Thursday, August 6, 2015
Sparks Fly and Flashes
From the post "High Frequency EMW From Laser" dated 31 Jul 2015 and post "Squeeze Laser" dated 28 Jul 2015, a material will give off both photons and EMWs when hit and deformed. The particles within it oscillating at \(\small{\theta=45^o}\) is moved to \(\small{\theta=43.535^o}\). The energy stored while oscillating at \(\small{\theta=45^o}\) is released at maximum intensity.
The EMWs emitted could account for sparks (charge flow) when metal are hit. And the photons released account for the flashes seen.
The EMWs emitted could account for sparks (charge flow) when metal are hit. And the photons released account for the flashes seen.
Tuesday, August 4, 2015
Monday, August 3, 2015
The Violet Hue
The problem with \(g^{+}\) and \(T^{+}\) particles generating photons is that both gravity and temperature will change the color of an object.
If high temperature moves colors towards the ultra violet spectrum, high gravity will also move colors towards the violet spectrum.
Red hot hotter or white hot hotter?
If high temperature moves colors towards the ultra violet spectrum, high gravity will also move colors towards the violet spectrum.
Red hot hotter or white hot hotter?