Time Dilation $\gamma(x)$ around a BlackHole

When the radius of earth ${r}_{e}$ is shrunk to ${r}_{eo}$ = 0.00886 m light will not escape from it.  The actual gravity of such a black hole is,

$g=-\cfrac{{G}_{o}}{(x+{r}_{eo})^2}$

${g}_{eo}=-\cfrac{{G}_{o}}{{r}_{eo}^2}$ = -5.07071e18 ms^-2

And the corresponding gravity equation is,

$g=-{g}_{eo}{e}^{-\cfrac{{g}_{eo}{r}_{eo}}{{G}_{o}}(x)}$

The corresponding time dilation field equation $\gamma(x)$ is,

$\gamma(x)=\sqrt{1-\cfrac{2{G}_{o}}{{c}^{2}{r}_{eo}}{e}^{-\cfrac{{g}_{eo}{r}_{eo}}{{G}_{o}}(x)}}$

$\cfrac{2{G}_{o}}{{c}^{2}{r}_{eo}}=1$

$\cfrac{{g}_{eo}{r}_{eo}}{{G}_{o}}=\cfrac{1}{{r}_{eo}}$ = 112.86681715575618 m^-1

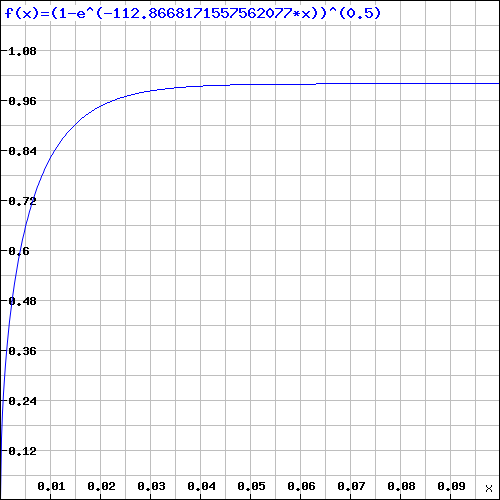
$\gamma(x)=\sqrt{1-e^{-112.866x}}$

This is a graph of time dilation $\gamma(x)$ = (1-e^(-112.866*x))^(0.5) around a black hole.  Time returns to normal very quickly at about 0.065 m.  So much for time travel around a black hole; a 6.5 cm disk around which time dilation occurs is way smaller than expected.