Pop Now, Pop Later

From the post "Amplitude, $A_n$" dated 23 Dec 2014 where it was proposed that the transition to an adjacent state occurs when the amplitude of the wave $\psi$ has increase to an extend where the perimeter of the resulting elliptical orbit is equal to the circular orbital perimeter of the next state.  This perimeter criteria is derived from the fact that $\psi$ is at constant light speed, when the perimeter of two orbits are the same, then $\psi$ on both orbits will have the same frequency and thus with Planck's relation ($E=h.f$), both will have the same energy.

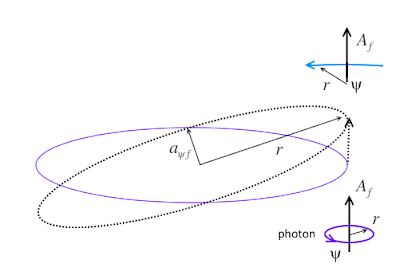
where,

$A_f=\sqrt{2}\sqrt{a^2_{\psi\,i}-a^2_{\psi\,f}}$   and

$r^{ 2 }=2a^2_{\psi\,i}-a^2_{\psi\,f}$

From the post "Touch And Go" dated 24 Dec 2014, transition to the state associated with $a_{\psi\,i}$ occurs when the long radius of the ellipse equals $a_{\psi\,i}$.  This occurs before the perimeters of the initial and final states are equal.

where,

$A_f=\sqrt{a^2_{\psi\,i}-a^2_{\psi\,f}}$   and

$r=a_{\psi\,i}$

If the emission of a photon occurs on transition to $r=\sqrt{2a^2_{\psi\,i}-a^2_{\psi\,f}}$ or $r=a_{\psi\,i}$, and $\psi$ thereafter orbit at $r=\sqrt{2a^2_{\psi\,i}-a^2_{\psi\,f}}$ or $r=a_{\psi\,i}$ with amplitude $A_i=0$, the energy in $A_f$ can be associated with the translation energy of the photon and, the oscillatory component of this wave (photon as a wave) is respectively $r=\sqrt{2a^2_{\psi\,i}-a^2_{\psi\,f}}$ or $r=a_{\psi\,i}$.

It could also be,

that the emission of a photon occurs only after $\psi$ returns to $a_{\psi\,f}$; after a timer interval $t$, having traveled along the elliptical path a quarter of the way at light speed, $c$.  In this case, the emitted photon has a oscillatory component at $a_{\psi\,f}$ only.

Which one of these occur?  The emitted photon is at $\sqrt{2a^2_{\psi\,i}-a^2_{\psi\,f}}$, $a_{\psi\,i}$ or $a_{\psi\,f}$.  If there is a constraint on $A_f$, below a threshold for which no emission occurs then all three possible scenarios can occur in different settings.  All three photons at their respective energies $E$ can be detected.

$E=h.\cfrac{2\pi.a_{\psi}}{c}$

What would be the constraint on $A_f$?  Goodnight.