From the table of data in the post "Ice, Water And Steam" dated 25 Oct 2017, the density of water at \(25^oC\) is \( 997.0479\,kgm^{-3}\) so,
\(v_{boom\,25^oC}=3.4354*\cfrac{997.0479}{10}=342.53\,ms^{-1}\)
This is the updated speed of a sonic boom.
Monday, October 30, 2017
Saturday, October 28, 2017
Red Herring Steamed
If we play this number game, water at temperature below \(80^oC\) (density \(971.8\,kgm^{-3}\)) but above \(60^oC\) (density \(983.2\,kgm^{-3}\)) has a density of \(975.96\,kgm^{-3}\) which gives,
\(v_{boom\,ice}=3.4354*\cfrac{975.96}{2*1+1*8}=335.28\,ms^{-1}\)
which would be lightning speed, quoted at \(750\,miles\,per\,hour\). Was magnetite a red herring? Earthquakes is due to lightning strikes on condensed underground steam?
How much energy can be released when lightning strikes condensed water at the above temperature range (\(\approx75^oC\) from www.engineeringtoolbox.com)?
\(v_{boom\,ice}=3.4354*\cfrac{975.96}{2*1+1*8}=335.28\,ms^{-1}\)
which would be lightning speed, quoted at \(750\,miles\,per\,hour\). Was magnetite a red herring? Earthquakes is due to lightning strikes on condensed underground steam?
How much energy can be released when lightning strikes condensed water at the above temperature range (\(\approx75^oC\) from www.engineeringtoolbox.com)?
Earthquake Is Nuclear?
Magnetite density \(Fe_3O_4\) = 5175 kgm-3
So,
\(v_{boom\,\small{Fe_3O_4}}=3.4354*\cfrac{5175}{3*26+4*8}=161.62\,ms^{-1}\) or \(581.83\,kmh^{-1}\)
but the speed of sound in magnetite \(v_{\small{sound}}\) = 5890 ms-1
The ratio,
\(\cfrac{v_{boom}}{v_{\small{sound}}}=\cfrac{161.62}{5890}=0.0274\)
Sound does not trigger earthquakes. Had the above ratio been an integer, earthquake could be triggered by sound reaching a magnetite layer causing it to collapse and changing its nature (post "Magnetite, Earthquake Crystals" dated 17 Aug 2017 and post "Magnetic Bonds And Stir" dated 17 Aug 2017). Earthquake would be much more frequent until magnetite is sufficiently far and insulated from sound on the ground level.
If instead of \(Fe_3O_4\) we have \(Fe_6O_8\) as a nucleus unit,
\(v_{boom\,\small{Fe_6O_8}}=3.4354*\cfrac{5175}{6*26+8*8}=80.81\,ms^{-1}\) or \(290.91\,kmh^{-1}\)
What would travel through the crystal strata at \(80.81\,ms^{-1}\) (or an integer multiple lower) and trigger a collapse?
Speed of lightning is quoted at about 335.28 ms-1, which is still too high compared to either \(v_{boom}\)'s above.
So,
\(v_{boom\,\small{Fe_3O_4}}=3.4354*\cfrac{5175}{3*26+4*8}=161.62\,ms^{-1}\) or \(581.83\,kmh^{-1}\)
but the speed of sound in magnetite \(v_{\small{sound}}\) = 5890 ms-1
The ratio,
\(\cfrac{v_{boom}}{v_{\small{sound}}}=\cfrac{161.62}{5890}=0.0274\)
Sound does not trigger earthquakes. Had the above ratio been an integer, earthquake could be triggered by sound reaching a magnetite layer causing it to collapse and changing its nature (post "Magnetite, Earthquake Crystals" dated 17 Aug 2017 and post "Magnetic Bonds And Stir" dated 17 Aug 2017). Earthquake would be much more frequent until magnetite is sufficiently far and insulated from sound on the ground level.
If instead of \(Fe_3O_4\) we have \(Fe_6O_8\) as a nucleus unit,
\(v_{boom\,\small{Fe_6O_8}}=3.4354*\cfrac{5175}{6*26+8*8}=80.81\,ms^{-1}\) or \(290.91\,kmh^{-1}\)
What would travel through the crystal strata at \(80.81\,ms^{-1}\) (or an integer multiple lower) and trigger a collapse?
Speed of lightning is quoted at about 335.28 ms-1, which is still too high compared to either \(v_{boom}\)'s above.
Wednesday, October 25, 2017
Ice, Water And Steam
These are density \((kgm^{-3})\) values for water at different temperature \(^oC\),
+100 958.4
+80 971.8
+60 983.2
+40 992.2
+30 995.6502
+25 997.0479
+22 997.7735
+20 998.2071
+15 999.1026
+10 999.7026
+4 999.9720
0 999.8395
−10 998.117
−20 993.547
−30 983.854
Steam has a density of \(0.6\,kgm^{-3}\) and ice has a density of \(916.7\,kgm^{-3}\). What shall we do?
Between ice of density \(916.7\,kgm^{-3}\), water at \(0^oC\) of density \( 999.8395\,kgm^{-3}\), and water at \(100^oC\) of density \( 958.4\,kgm^{-3}\) increasing temperature will hit \(v_{boom\,ice}\) of ice first then with increasing temperature as density drops, \(v_{boom\,100}\) of water at \(100^oC\).
\(v_{boom\,ice}=3.4354*\cfrac{916.7}{10}=314.9\,ms^{-1}\)
\(v_{boom\,100}=3.4354*\cfrac{958.4}{10}=329.25\,ms^{-1}\)
\(329.25\,ms^{-1}\) is very close to the sonic boom, \(v_{boom\,100}\) is the reason why the spout of the kettle made to taper, whistles when water boils. A narrowed opening increases \(v_{boom\,100}\) to a sonic boom. Of all the particles involved the most likely candidates responsible for the whistle are \(g^{+}\) and \(g^{-}\), because steam escaping from the spout of a boiling kettle is not at sonic boom speed, but the disintegrated particles are.
Latent heat is nuclear. Latent heat is due to resonance at \(v_{boom}\). Latent heat is not reversible.
Logic takes a second place when you guess. Courage takes first place.
+100 958.4
+80 971.8
+60 983.2
+40 992.2
+30 995.6502
+25 997.0479
+22 997.7735
+20 998.2071
+15 999.1026
+10 999.7026
+4 999.9720
0 999.8395
−10 998.117
−20 993.547
−30 983.854
Steam has a density of \(0.6\,kgm^{-3}\) and ice has a density of \(916.7\,kgm^{-3}\). What shall we do?
Between ice of density \(916.7\,kgm^{-3}\), water at \(0^oC\) of density \( 999.8395\,kgm^{-3}\), and water at \(100^oC\) of density \( 958.4\,kgm^{-3}\) increasing temperature will hit \(v_{boom\,ice}\) of ice first then with increasing temperature as density drops, \(v_{boom\,100}\) of water at \(100^oC\).
\(v_{boom\,ice}=3.4354*\cfrac{916.7}{10}=314.9\,ms^{-1}\)
\(v_{boom\,100}=3.4354*\cfrac{958.4}{10}=329.25\,ms^{-1}\)
\(329.25\,ms^{-1}\) is very close to the sonic boom, \(v_{boom\,100}\) is the reason why the spout of the kettle made to taper, whistles when water boils. A narrowed opening increases \(v_{boom\,100}\) to a sonic boom. Of all the particles involved the most likely candidates responsible for the whistle are \(g^{+}\) and \(g^{-}\), because steam escaping from the spout of a boiling kettle is not at sonic boom speed, but the disintegrated particles are.
Latent heat is nuclear. Latent heat is due to resonance at \(v_{boom}\). Latent heat is not reversible.
Logic takes a second place when you guess. Courage takes first place.
This Is Not Melting
If auto-ignition temperature is the temperature when the vapor molecules/atoms just achieve boom velocity, instantaneously as their vibration energy increases with temperature, then we have a good correspondence of temperature of the vapor given its molecular/atomic mass, and kinetic energy that was previously used to define temperature. As in
\(PV=nRT\)
we have instead,
\(T=density*f(v_{boom})\)
where \(T\) is temperature and \(f(v_{boom})\) is some function of \(v_{boom}\). Consider,
\(KE\equiv density*f(v_{boom})\)
so,
\(KE=\cfrac{1}{2}*density*v_{boom}^2\)
this would be kinetic energy per unit volume, but,
\(v_{boom}=3.4354*density*\cfrac{1}{particle\,count\,per\,type}\)
so,
\(KE=\cfrac{3.4354^2}{2}*density^3*\cfrac{1}{(particle\,count\,per\,type)^2}\)
And in the case of basic elements,
\(KE=density^3*\cfrac{5.901}{(atomic\,\,number)^2}\)
where the density (cubed) of the elements changes with \(T\). A plot of \(T\) vs \(v_{boom}\) of various density will give \(f(v_{boom})\) or the function f(x), from which we may then infer \(KE=g(T)\) where \(g(T)\) is a function of \(T\). Temperature \(T\) here then, as intended is a measure of the vibrational kinetic energy within the element.
This seemingly is a definition of temperature without the explicit involvement of temperature particles, derived from the vibrational kinetic energy of the atoms in an elements. A sentinel point in this definition is \(T_{boom}\), the temperature at which \(v_{boom}\) is achieved.
This is not melting, but it would be interesting if \(T_{boom}\) occurs before the melting point.
Or is it? Melting? \(v_{boom}\) changes density and could account for the energy released during phase change. There is a \(v_{boom}\) from solid to liquid, a different \(v_{boom}\) from liquid to gas and yet another value of \(v_{boom}\) for the gas as it disintegrate. Different \(v_{boom}\) values for different densities of the element/compound.
Is \(v_{boom}\) responsible for phase change? Phase change would then be nuclear. Boiling water for tea would then be nuclear.
\(PV=nRT\)
we have instead,
\(T=density*f(v_{boom})\)
where \(T\) is temperature and \(f(v_{boom})\) is some function of \(v_{boom}\). Consider,
\(KE\equiv density*f(v_{boom})\)
so,
\(KE=\cfrac{1}{2}*density*v_{boom}^2\)
this would be kinetic energy per unit volume, but,
\(v_{boom}=3.4354*density*\cfrac{1}{particle\,count\,per\,type}\)
so,
\(KE=\cfrac{3.4354^2}{2}*density^3*\cfrac{1}{(particle\,count\,per\,type)^2}\)
And in the case of basic elements,
\(KE=density^3*\cfrac{5.901}{(atomic\,\,number)^2}\)
where the density (cubed) of the elements changes with \(T\). A plot of \(T\) vs \(v_{boom}\) of various density will give \(f(v_{boom})\) or the function f(x), from which we may then infer \(KE=g(T)\) where \(g(T)\) is a function of \(T\). Temperature \(T\) here then, as intended is a measure of the vibrational kinetic energy within the element.
This seemingly is a definition of temperature without the explicit involvement of temperature particles, derived from the vibrational kinetic energy of the atoms in an elements. A sentinel point in this definition is \(T_{boom}\), the temperature at which \(v_{boom}\) is achieved.
This is not melting, but it would be interesting if \(T_{boom}\) occurs before the melting point.
Or is it? Melting? \(v_{boom}\) changes density and could account for the energy released during phase change. There is a \(v_{boom}\) from solid to liquid, a different \(v_{boom}\) from liquid to gas and yet another value of \(v_{boom}\) for the gas as it disintegrate. Different \(v_{boom}\) values for different densities of the element/compound.
Is \(v_{boom}\) responsible for phase change? Phase change would then be nuclear. Boiling water for tea would then be nuclear.
Nuclear Stability
From the post "Gasoline Boom And Diesel Boom" dated 23 Oct 2017,
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*density*\cfrac{1}{particle\,count\,per\,type}\)
where we obtain the boom velocity,
\(v_{boom}=3.4354*density*\cfrac{1}{particle\,count\,per\,type}\)
Obviously the higher this velocity is the greater the stability of the material is with regard to both temperature and collisions. The factor,
\(S_v=density*\cfrac{1}{particle\,count\,per\,type}\)
is then indicative of the relative stability of the materials concerned. In the case of the Elements,
\(S_v=\cfrac{element\,\,density}{atomic\,\,number}\)
where the density of the elements is at room temperature.
\(S_v\) is indicative of the relative stability of the elements. \(S_v\) is nuclear stability as we are concern here with the interactions of \(\psi\) particles. A \(S_v\) vs atomic number plot is given below,
This is not as expected; it is not in the profile of nuclear binding energy vs number of nucleons. In this plot, data was not available to \(Z=85\) and \(Z=87\), a break occurs along the atomic number axis. Elements that are gases under normal conditions are low in the plot. The most stable element is \(^5B\), Boron, followed by \(^4Be\), Beryllium.
Note: Nuclear binding energy, confined to the nucleus of an atomic, has nothing to do with material density, a property concerning the compactness between atoms. Maybe, nuclear binding energy is the same for all nucleus, but the element's density (an attribute derived from the space between atoms) that endows the element with strength against disintegration. Stability is a group thing.
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*density*\cfrac{1}{particle\,count\,per\,type}\)
where we obtain the boom velocity,
\(v_{boom}=3.4354*density*\cfrac{1}{particle\,count\,per\,type}\)
Obviously the higher this velocity is the greater the stability of the material is with regard to both temperature and collisions. The factor,
\(S_v=density*\cfrac{1}{particle\,count\,per\,type}\)
is then indicative of the relative stability of the materials concerned. In the case of the Elements,
\(S_v=\cfrac{element\,\,density}{atomic\,\,number}\)
where the density of the elements is at room temperature.
\(S_v\) is indicative of the relative stability of the elements. \(S_v\) is nuclear stability as we are concern here with the interactions of \(\psi\) particles. A \(S_v\) vs atomic number plot is given below,
This is not as expected; it is not in the profile of nuclear binding energy vs number of nucleons. In this plot, data was not available to \(Z=85\) and \(Z=87\), a break occurs along the atomic number axis. Elements that are gases under normal conditions are low in the plot. The most stable element is \(^5B\), Boron, followed by \(^4Be\), Beryllium.
Note: Nuclear binding energy, confined to the nucleus of an atomic, has nothing to do with material density, a property concerning the compactness between atoms. Maybe, nuclear binding energy is the same for all nucleus, but the element's density (an attribute derived from the space between atoms) that endows the element with strength against disintegration. Stability is a group thing.
Tuesday, October 24, 2017
Fire Starter
I have seen this before,
pumping the piston with short strokes while holding the open end with the other hand will ignite the dry material inside. The trick is to get the speed just right.
If we apply,
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*density*\cfrac{1}{particle\,count\,per\,type}\)
from the post "Sonic Boom" dated 13 Oct 2017 to kerosene of average density of \(795\,kgm^{-3}\) and formula \(C_{13.5}H_{29}\)
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*795*\cfrac{1}{13.5*6+29*1}\)
we have \(v_{boom}=24.83\,ms^{-1}\) or \(89.38\,kmh^{-1}\)
And when kerosene is diluted with \(70\%\) gasoline, its density drops to \(30\%\) with its average molecular formula unchanged,
\(v_{boom}=24.83*0.3\)
\(v_{boom}=7.45\,ms^{-1}\) or \(26.81\,kmh^{-1}\)
Gasoline in this mixture will have a reduced density by \(70\%\), and so a similarly reduced boom speed of,
\(v_{boom}=37.46*0.7\)
\(v_{boom}=26.22\,ms^{-1}\) or \(94.40\,kmh^{-1}\)
If boom speed is an indication of flash point (wrong not flash point, instead, kindle point), this is how mixing fuel reduces flash point. Molecular vibrations is directly proportional to temperature. At high temperature, in high vibrations, we achieve boom speed and the fuel is nuclear.
Note: Auto-ignition temperature or kindling point of a substance is the lowest temperature at which it spontaneously ignites in normal atmosphere without an external source of ignition, such as a flame or spark. Is should be kindling point and not flash point that is referred to above.
pumping the piston with short strokes while holding the open end with the other hand will ignite the dry material inside. The trick is to get the speed just right.
If we apply,
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*density*\cfrac{1}{particle\,count\,per\,type}\)
from the post "Sonic Boom" dated 13 Oct 2017 to kerosene of average density of \(795\,kgm^{-3}\) and formula \(C_{13.5}H_{29}\)
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*795*\cfrac{1}{13.5*6+29*1}\)
we have \(v_{boom}=24.83\,ms^{-1}\) or \(89.38\,kmh^{-1}\)
And when kerosene is diluted with \(70\%\) gasoline, its density drops to \(30\%\) with its average molecular formula unchanged,
\(v_{boom}=24.83*0.3\)
\(v_{boom}=7.45\,ms^{-1}\) or \(26.81\,kmh^{-1}\)
Gasoline in this mixture will have a reduced density by \(70\%\), and so a similarly reduced boom speed of,
\(v_{boom}=37.46*0.7\)
\(v_{boom}=26.22\,ms^{-1}\) or \(94.40\,kmh^{-1}\)
If boom speed is an indication of flash point (wrong not flash point, instead, kindle point), this is how mixing fuel reduces flash point. Molecular vibrations is directly proportional to temperature. At high temperature, in high vibrations, we achieve boom speed and the fuel is nuclear.
Note: Auto-ignition temperature or kindling point of a substance is the lowest temperature at which it spontaneously ignites in normal atmosphere without an external source of ignition, such as a flame or spark. Is should be kindling point and not flash point that is referred to above.
Monday, October 23, 2017
Nuclear Jet Engine
How to achieve a constant boom push at the fuel? A piston driven by circular motion will be sinusoidal...A jet engine! The fans provide the constant push speed. The fuel disintegrates.
How then to better utilize the various particles as the result of fuel disintegration? Conventional view of a jet engine only provides thrust, but all particles are present \((g^{+},\,g^{-})\) \((T^{+},\,T^{-})\) and \((p^{+},\,e^{-})\) as the fuel disintegrate. An average net accumulation of \(g^{+}\) particles in the jet provides lift, as smaller \(g^{-}\) particles are driven away quickly. What about the other types of particles? As \(g^{+}\) particles are driven into the open, it seems to be too wasteful. We are speculating that the jet engine provides lift by itself without Bernoulli principle being applied to an advancing wing driven by the engine's thrust.
Firstly, a jet engine working around a particular push speed, is best run with fuel of a narrow range of carbon number; a piston engine that provides a wide range of push speeds as the drive is in circular motion, is best run with fuel that has a wide range of carbon number.
Ignition point should not be a concern, at the correct boom speed. Ignition as the fuel nuclear disintegrate is guaranteed, theoretically. Ignition is wasteful as the fuel burns.
Should fuel be allowed to ignite at all? \(g^{+}\) particles provides lift and \(T^{+}\) particles provides thrust. Maybe...
How then to better utilize the various particles as the result of fuel disintegration? Conventional view of a jet engine only provides thrust, but all particles are present \((g^{+},\,g^{-})\) \((T^{+},\,T^{-})\) and \((p^{+},\,e^{-})\) as the fuel disintegrate. An average net accumulation of \(g^{+}\) particles in the jet provides lift, as smaller \(g^{-}\) particles are driven away quickly. What about the other types of particles? As \(g^{+}\) particles are driven into the open, it seems to be too wasteful. We are speculating that the jet engine provides lift by itself without Bernoulli principle being applied to an advancing wing driven by the engine's thrust.
Firstly, a jet engine working around a particular push speed, is best run with fuel of a narrow range of carbon number; a piston engine that provides a wide range of push speeds as the drive is in circular motion, is best run with fuel that has a wide range of carbon number.
Ignition point should not be a concern, at the correct boom speed. Ignition as the fuel nuclear disintegrate is guaranteed, theoretically. Ignition is wasteful as the fuel burns.
Should fuel be allowed to ignite at all? \(g^{+}\) particles provides lift and \(T^{+}\) particles provides thrust. Maybe...
Gasoline Boom And Diesel Boom
If we were to apply,
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*1000*\cfrac{1}{10}\)
or more clearly,
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*density*\cfrac{1}{particle\,count\,per\,type}\)
from the post "Sonic Boom" dated 13 Oct 2017, to common diesel fuel of average chemical formula \(C_{12}H_{24}\) and a density of \(840\,kgm^{-3}\).
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*840*\cfrac{1}{12*6+24*1}\)
Note: If we need high speed fuel, the trade off is between low particle count per type of particle and high density fuel. Density decreases with low particle count. Coil up fuel with low particle count but high density comes to mind, but conventional view on hydrocarbons that have many branches is that they burn less effectively. Why should fuel be burning?
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*1000*\cfrac{1}{10}\)
or more clearly,
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*density*\cfrac{1}{particle\,count\,per\,type}\)
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*840*\cfrac{1}{12*6+24*1}\)
we have a diesel boom at \(30.05\,ms^{-1}\) or \(108.22\,kmh^{-1}\) Ooops
And if we apply the expression to gasoline of density \(719.7\,kgm^{-3}\) and on average (\(C_{4}-C_{12}\)), \(C_{8}H_{18}\),
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*719.7*\cfrac{1}{8*6+18*1}\)
we have a gasoline boom at \(37.46\,ms^{-1}\) or \(134.86\,kmh^{-1}\) Ooops
These are not cruise speeds. But these speeds suggest that both gasoline and diesel ignite without a spark when pushed at their respective boom speeds. For maximum energy yield, both boom speed should be sustained; at maximum efficiency the energy conversion is nuclear! For less that perfect efficiency (sinusoidal boom speed), the fuel combustion in the heat produced, produces waste gas.
Do we really need the engine to go nuclear?
Note: If we need high speed fuel, the trade off is between low particle count per type of particle and high density fuel. Density decreases with low particle count. Coil up fuel with low particle count but high density comes to mind, but conventional view on hydrocarbons that have many branches is that they burn less effectively. Why should fuel be burning?
Sunday, October 22, 2017
Wise Up Reaction
It is not fusion that is explosive nor is it big particles disintegrating into basic particles that is necessarily explosive, it is chain reaction, where an action triggers one or more other actions that a cascade of energy is released.
So, let the sonic boom be. \(^{235}U\) as a vapor with a specific density can be driven to an disintegration speed. It is the chain reaction that occurs as emissions from the elements' disintegration triggers more disintegrations that is explosive.
Enough said.
So, let the sonic boom be. \(^{235}U\) as a vapor with a specific density can be driven to an disintegration speed. It is the chain reaction that occurs as emissions from the elements' disintegration triggers more disintegrations that is explosive.
Enough said.
Thursday, October 19, 2017
Hydrogen Bomb
This is the newest reincarnation of a hydrogen bomb,
Fusion occurs at the tip of the vortex. Go ahead blow yourselves up.
\(\cfrac{15.43}{2}\), corrects for relative velocities as opposing streams from opposite slanted surface of the triangular cone collide.
Fusion occurs at the tip of the vortex. Go ahead blow yourselves up.
\(\cfrac{15.43}{2}\), corrects for relative velocities as opposing streams from opposite slanted surface of the triangular cone collide.
It Was Nuclear
You will not believe that this old Chinese contraption that feeds a stove fire is nuclear,
The schematic of which for the mad scientist ready to blow up this world,
The piston is pulled for two seconds and then pushed for two seconds. If we consider \(H_2\), from the post "A Small Boom" dated 16 Oct 2017,
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*0.08988*\cfrac{1}{2}\)
\(v_{\small{H_2\,boom}}=0.1543\,ms^{-1}=0.555\,kmh^{-1}\)
we might add the dimension \(2\times15.43\,cm\) for moving hydrogen gas in the pump. (\(2\times28.6\,cm\) for pumping nitrogen and \(2\times30.68\,cm\) for pumping oxygen.
We are doomed...A nuclear reactor in every household!
The schematic of which for the mad scientist ready to blow up this world,
The piston is pulled for two seconds and then pushed for two seconds. If we consider \(H_2\), from the post "A Small Boom" dated 16 Oct 2017,
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*0.08988*\cfrac{1}{2}\)
\(v_{\small{H_2\,boom}}=0.1543\,ms^{-1}=0.555\,kmh^{-1}\)
we might add the dimension \(2\times15.43\,cm\) for moving hydrogen gas in the pump. (\(2\times28.6\,cm\) for pumping nitrogen and \(2\times30.68\,cm\) for pumping oxygen.
We are doomed...A nuclear reactor in every household!
Wednesday, October 18, 2017
Smaller Because of Resistance
\(\varepsilon_o\)!
The spectra lines are measured in space. \(a_{\psi}\) in the post "The Path Also Taken" dated 18 Oct 2017 and X Ray, Inner Electron Cloud And Just As Shocking TWO" dated 15 Oct 2017, is in a solid. The concept of \(\varepsilon\) is applicable only as a resistance to the extent of \(\psi\) in a soild. That is why from the X-ray data, \(a_{\psi}\) calculated is smaller from spectra lines data; \(\psi\) experiences more resistance to extend in a solid.
Goodnight.
The spectra lines are measured in space. \(a_{\psi}\) in the post "The Path Also Taken" dated 18 Oct 2017 and X Ray, Inner Electron Cloud And Just As Shocking TWO" dated 15 Oct 2017, is in a solid. The concept of \(\varepsilon\) is applicable only as a resistance to the extent of \(\psi\) in a soild. That is why from the X-ray data, \(a_{\psi}\) calculated is smaller from spectra lines data; \(\psi\) experiences more resistance to extend in a solid.
Goodnight.
The Path Also Taken
If we use,
\(\sqrt[3]{N}.2\pi a_{\psi\,c}=\lambda_\beta\)
and
\(\cfrac{ave.\,E\alpha}{E\beta}=\sqrt[3]{\cfrac{N+1}{N}}\)
\(\cfrac{N+1}{N}=\left(\cfrac{ave.\,E\alpha}{E\beta}\right)^3\)
\(\cfrac{N+1}{N}=(\cfrac{1.54184}{1.39222})^3=1.36\)
\(N=9\)
since,
\(\cfrac{9+1}{9}=1.37\)
So,
\(a_{\psi\,c}=\cfrac{\lambda_\beta}{\sqrt[3]{N}.2\pi }\)
\(a_{\psi\,c}=\cfrac{1.39222}{\sqrt[3]{9}.2\pi }\)
\(a_{\psi\,c}=0.10493e-10=0.010493\,\,nm\)
This is the first time we have actually obtained \(a_{\psi\,\,c}\) from experimental data. It is however, way smaller than expected, because,
\(\sqrt[3]{N}.a_{\psi\,c}=a_{\psi\,\small{N}}\)
when \(N=77\)
\(a_{\psi\,\small{N}}=4.4639e-11\,\,m\)
which smaller than the values for \(a_{\psi}\) obtained from hydrogen spectra lines experiments, in the post "Sizing Them Up" dated 3 Dec 2014.
Nonetheless,
\(f_{res}=0.061\cfrac { c }{ a_{\psi} }\)
\(f_{res}=0.061\cfrac { 299792458 }{ \sqrt[3]{9}*0.10493e-10 }\)
\(f_{res}=0.83786*10^{18}\,\,Hz\)
which is nine times less than the previously calculated value of \(f_{res}=7.473*10^{18} Hz\). And so the current that would cause resonance is,
\(I_{res}=\cfrac{1.1974}{9}=0.13304\,\,A\)
This current reduced by an integer divisor will also cause resonance but slower. Currents higher by an integer multiplier than \(I_{res}\) will not caused resonance. But it is,
\(\sqrt[3]{N}.a_{\psi\,c}=\sqrt[3]{9}*0.10493e-10=2.1826e-11\)
that is resonating. What is this entity than is about nine times bigger than the previous value,
\(a_{\psi}=0.2447e-11\)
Does,
\(\sqrt[3]{N}.2\pi a_{\psi\,c}=\lambda_\beta\)
make sense in the first place? Or,
\(N.2\pi a_{\psi}=\lambda_\beta\)
What is happening here? What are we setting into resonance? \(a_{\psi\,c}\), \(\sqrt[3]{N}a_{\psi\,c}\) or \(Na_{\psi}\)?
The lower values for \(a_{\psi\,c}\) suggests that,
\(\cfrac{a_{\psi\,1}}{a_{\psi\,1}}=\left(\cfrac{N_1}{N_2}\right)^3\)
maybe wrong; that when particles merge, the total volume of \(\psi\) may not be conserved.
The expression, \(N.a_{\psi}\) suggests that,
the particles, \(a_{\psi}\) are stacked up. Which would imply that X-ray emission is along an axis where \(N\) particles stack up; perpendicularly outwards, across \(N\).
If \(a_{\psi}\) being stack up is true, then it would be impossible to obtain X ray from atomized \(Cu\) vapor nor non-homogeneous alloys of \(Cu\) where \(a_{\psi}\) cannot stack up.
\(\sqrt[3]{N}.2\pi a_{\psi\,c}=\lambda_\beta\)
and
\(\cfrac{ave.\,E\alpha}{E\beta}=\sqrt[3]{\cfrac{N+1}{N}}\)
\(\cfrac{N+1}{N}=\left(\cfrac{ave.\,E\alpha}{E\beta}\right)^3\)
\(\cfrac{N+1}{N}=(\cfrac{1.54184}{1.39222})^3=1.36\)
\(N=9\)
since,
\(\cfrac{9+1}{9}=1.37\)
So,
\(a_{\psi\,c}=\cfrac{\lambda_\beta}{\sqrt[3]{N}.2\pi }\)
\(a_{\psi\,c}=\cfrac{1.39222}{\sqrt[3]{9}.2\pi }\)
\(a_{\psi\,c}=0.10493e-10=0.010493\,\,nm\)
This is the first time we have actually obtained \(a_{\psi\,\,c}\) from experimental data. It is however, way smaller than expected, because,
\(\sqrt[3]{N}.a_{\psi\,c}=a_{\psi\,\small{N}}\)
when \(N=77\)
\(a_{\psi\,\small{N}}=4.4639e-11\,\,m\)
which smaller than the values for \(a_{\psi}\) obtained from hydrogen spectra lines experiments, in the post "Sizing Them Up" dated 3 Dec 2014.
Nonetheless,
\(f_{res}=0.061\cfrac { c }{ a_{\psi} }\)
\(f_{res}=0.061\cfrac { 299792458 }{ \sqrt[3]{9}*0.10493e-10 }\)
\(f_{res}=0.83786*10^{18}\,\,Hz\)
which is nine times less than the previously calculated value of \(f_{res}=7.473*10^{18} Hz\). And so the current that would cause resonance is,
\(I_{res}=\cfrac{1.1974}{9}=0.13304\,\,A\)
This current reduced by an integer divisor will also cause resonance but slower. Currents higher by an integer multiplier than \(I_{res}\) will not caused resonance. But it is,
\(\sqrt[3]{N}.a_{\psi\,c}=\sqrt[3]{9}*0.10493e-10=2.1826e-11\)
that is resonating. What is this entity than is about nine times bigger than the previous value,
\(a_{\psi}=0.2447e-11\)
Does,
\(\sqrt[3]{N}.2\pi a_{\psi\,c}=\lambda_\beta\)
make sense in the first place? Or,
\(N.2\pi a_{\psi}=\lambda_\beta\)
What is happening here? What are we setting into resonance? \(a_{\psi\,c}\), \(\sqrt[3]{N}a_{\psi\,c}\) or \(Na_{\psi}\)?
The lower values for \(a_{\psi\,c}\) suggests that,
\(\cfrac{a_{\psi\,1}}{a_{\psi\,1}}=\left(\cfrac{N_1}{N_2}\right)^3\)
maybe wrong; that when particles merge, the total volume of \(\psi\) may not be conserved.
The expression, \(N.a_{\psi}\) suggests that,
the particles, \(a_{\psi}\) are stacked up. Which would imply that X-ray emission is along an axis where \(N\) particles stack up; perpendicularly outwards, across \(N\).
If \(a_{\psi}\) being stack up is true, then it would be impossible to obtain X ray from atomized \(Cu\) vapor nor non-homogeneous alloys of \(Cu\) where \(a_{\psi}\) cannot stack up.
Tuesday, October 17, 2017
Venus Pulsing
A closer look at \(f\propto \cfrac{1}{m}\) leads to the post "Twinkle, Twinkle Little Stars" dated 25 Jul 2014,
\(f=\cfrac{1}{2\pi}\sqrt{\cfrac{g_{p}}{r_{p}}}\)
and Venus adjusted surface gravity, \(g_v=0.02586\,\,kms^{-2}\) and its radius \(r_v=6052\,\,km\) which give,
\(f=\cfrac{1}{2\pi}\sqrt{\cfrac{0.02586}{6052}}=0.0003290\,\,s^{-1}\)
which is about one pulse in \(3039.6\,s\) or one pulse in \(50.66\,mins\). Do not confusion this pulse with atmospheric disturbance.
\(f=\cfrac{1}{2\pi}\sqrt{\cfrac{g_{p}}{r_{p}}}\)
and Venus adjusted surface gravity, \(g_v=0.02586\,\,kms^{-2}\) and its radius \(r_v=6052\,\,km\) which give,
\(f=\cfrac{1}{2\pi}\sqrt{\cfrac{0.02586}{6052}}=0.0003290\,\,s^{-1}\)
which is about one pulse in \(3039.6\,s\) or one pulse in \(50.66\,mins\). Do not confusion this pulse with atmospheric disturbance.
Monday, October 16, 2017
To Assume Not Much
In the post "X Ray, Inner Electron Cloud And Just As Shocking TWO" dated 15 Oct 2017, the expression,
\(N.2\pi a_{\psi}=\lambda_\beta\)
was formulated before \(a_{\psi\,c}\) was discovered. We might have,
\(\sqrt[3]{N}.2\pi a_{\psi\,c}=\lambda_\beta\)
from,
\(\sqrt[3]{\cfrac{1}{N}}=\cfrac{a_{\psi\,c}}{a_{\psi\,\small{N}}}\)
and so,
\(\cfrac{ave.\,E\alpha}{E\beta}=\sqrt[3]{\cfrac{N+1}{N}}\)
From which we may find \(a_{\psi\,c}\), but for the resonance of the electron cloud that we seek, we need the electron cloud \(a_{\psi\,cloud}\),
not \(\sqrt[3]{N}.a_{\psi\,c}\) nor \(a_{\psi\,\,c}\)
The rationale for making the estimate \(N\) and \(N+1\) is that given,
\(N.2\pi a_{\psi}=\lambda_\beta\)
and
\((N+1)2\pi a_{\psi}=\lambda_{ave\,\,\alpha}\)
no matter what \(a_{\psi}\) is, the addition of one more particle pushes \(a_{\psi}\) outwards and the allowable energy states splits into two narrowly spaced energy states. When the resonance frequency is applied using an appropriate current, the particles injected resonate. X-ray radiations at the \(E\alpha\) values will dominate and is adjusted as the current is reduced by an integer divisor.
This way, there is no need to assume that \(a_{\psi}=a_{\psi\,c}\). The only assumption is that the \(E\alpha\)'s and \(E\beta\) are consecutive, due to the injection and emission of one particle \(a_{\psi}\).
Furthermore,
\(N.2\pi a_{\psi}=\lambda_\beta\)
\((N+1)2\pi a_{\psi}=\lambda_{ave\,\,\alpha}\)
\((\cfrac{\lambda_\beta}{2\pi a_{\psi}}+1)2\pi a_{\psi}=\lambda_{ave\,\,\alpha}\)
\(\lambda_\beta+2\pi a_{\psi}=\lambda_{ave\,\,\alpha}\)
If \(f \propto \cfrac{1}{m}\) (the approximation part) such that,
\(m.f=\,\,constant\)
\(m_\beta c.f_{\beta}.\lambda_\beta+m_\psi c.f_{\psi}.2\pi a_{\psi}=(m_\beta+m_\psi) c.f_{ave\,\,\alpha}.\lambda_{ave\,\,\alpha}\)
that the total work done in going around \(\lambda_\beta\) and around the additional particle \(a_{\psi} \), is the work done going around \(\lambda_{ave\,\,\alpha}\).
Furthermore,
\(N.2\pi a_{\psi}=\lambda_\beta\)
\((N+1)2\pi a_{\psi}=\lambda_{ave\,\,\alpha}\)
\((\cfrac{\lambda_\beta}{2\pi a_{\psi}}+1)2\pi a_{\psi}=\lambda_{ave\,\,\alpha}\)
\(\lambda_\beta+2\pi a_{\psi}=\lambda_{ave\,\,\alpha}\)
If \(f \propto \cfrac{1}{m}\) (the approximation part) such that,
\(m.f=\,\,constant\)
\(m_\beta c.f_{\beta}.\lambda_\beta+m_\psi c.f_{\psi}.2\pi a_{\psi}=(m_\beta+m_\psi) c.f_{ave\,\,\alpha}.\lambda_{ave\,\,\alpha}\)
that the total work done in going around \(\lambda_\beta\) and around the additional particle \(a_{\psi} \), is the work done going around \(\lambda_{ave\,\,\alpha}\).
Goodnight.
A Small Boom
From the post "Sonic Boom" dated 14 Oct 2017, for water (not steam),
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*1000*\cfrac{1}{10}\)
If we replace water with the most abundant element in air, nitrogen, \(N_2\),
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*1.165*\cfrac{1}{14}\)
which has a density of \(1.165\,\, kgm^{-3}\) with a total of 14 particles (adding Atomic Numbers) in the molecule. We have
\(E_{input/proton}=\cfrac{1}{2}(one\,\,particle)*c^{ 2 }*(one\,\,unit\,\,volume)*0.286\)
we have a low boom at \(0.286\,\, ms^{-1}\) or \(1.03\,\, kmh^{-1}\)
what is the significance of this speed?
This calculations however is based on resonance, not of a minimum threshold, beyond \(343.5\,ms^{-1}\) or \(1.03\,\, kmh^{-1}\) resistance due to the booms should decrease rapidly. The \(Q\) factor of the underlying resonance phenomenon determines the rise and fall of resistance around the boom values.
The nitrogen boom can be observed as a small boat accelerates to high speed. This boom is experienced as a bump in the wave as the bow lifts due to the boom. But as speed increases the resistance decays quickly. If the boat remains at nitrogen boom speed, \(1.03\,\, kmh^{-1}\), it will flip over, bow backwards.
If we are able to obtain the Q profiles as speed varies around \(343.5\,\,ms^{-1}\) or \(1.03\,\, kmh^{-1}\), the Q factors are indicative of the underlying resonance phenomena.
Good night.
Note: We also have for \(O_2\),
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*1.429*\cfrac{1}{16}\)
\(v_{\small{O_2\,boom}}=0.3068\,ms^{-1}=1.10\,kmh^{-1}\)
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*1000*\cfrac{1}{10}\)
If we replace water with the most abundant element in air, nitrogen, \(N_2\),
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*1.165*\cfrac{1}{14}\)
which has a density of \(1.165\,\, kgm^{-3}\) with a total of 14 particles (adding Atomic Numbers) in the molecule. We have
\(E_{input/proton}=\cfrac{1}{2}(one\,\,particle)*c^{ 2 }*(one\,\,unit\,\,volume)*0.286\)
we have a low boom at \(0.286\,\, ms^{-1}\) or \(1.03\,\, kmh^{-1}\)
what is the significance of this speed?
This calculations however is based on resonance, not of a minimum threshold, beyond \(343.5\,ms^{-1}\) or \(1.03\,\, kmh^{-1}\) resistance due to the booms should decrease rapidly. The \(Q\) factor of the underlying resonance phenomenon determines the rise and fall of resistance around the boom values.
The nitrogen boom can be observed as a small boat accelerates to high speed. This boom is experienced as a bump in the wave as the bow lifts due to the boom. But as speed increases the resistance decays quickly. If the boat remains at nitrogen boom speed, \(1.03\,\, kmh^{-1}\), it will flip over, bow backwards.
If we are able to obtain the Q profiles as speed varies around \(343.5\,\,ms^{-1}\) or \(1.03\,\, kmh^{-1}\), the Q factors are indicative of the underlying resonance phenomena.
Good night.
Note: We also have for \(O_2\),
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*1.429*\cfrac{1}{16}\)
\(v_{\small{O_2\,boom}}=0.3068\,ms^{-1}=1.10\,kmh^{-1}\)
Sunday, October 15, 2017
X Ray, Inner Electron Cloud And Just As Shocking TWO
May this revision will explain better with a diagram and a change to the notation for the number of \(a_\psi\) that constitute the electron cloud, \(N\).
From the post "A Shield" and "A \(\Psi\) Gun" both dated 27 May 2016,
\(f_{res}=0.061\cfrac { c }{ a_{\psi} }\)
\(a_{\psi}\) is driven to oscillate about \(x=\cfrac{\pi \sqrt { 2{ mc^{ 2 } } } }{G}\). The work done in moving \(\psi\) forward is given by,
\(\int_{\pi-A_w}^{\pi+A_p}{tanh(x)}dx\)
On the return, at position \(x\), \(\psi\) radiates this energy gained. The energy radiated is,
\(X=\int_{\pi-A_w}^{\pi+A_p}{tanh(x)}dx-\int_{\pi-A_w}^{x}{tanh(x)}dx\)
\(X=\left[ ln(cosh(x)) \right] _{ \pi -A_{ w } }^{ \pi +A_{ p } }-\left[ ln(cosh(x)) \right] _{ \pi -A_{ w } }^{ x }\)
\( X=X_{ o }-ln(cosh(x))\)
with, \( X_{ o }=ln(cosh(\pi +A_{ p }))\)
A plot of log(cosh(pi+2))-log(cosh(x)) shows an almost linear decrease in energy radiated given the position \(x=a_{\psi}\),
\(U_{1/2}\) marks the value of \(a_{\psi}\) where work done travelling on the left and right side are equal.
We would also expect an almost linear increase in \(X\) as the amplitude \(A_p\) is increased at any given position, for example \(x=\pi\). ie
\( X_{\pi}=ln(cosh(x_{1/2} +x))-ln(cosh(x_{1/2}))\)
is almost increasing linearly. In addition, when \(a_{\psi}\) drops below
\(n.2\pi f_n a_{\psi}=c\) --- (*)
where the particle(s) is in resonance along \(2\pi a_{\psi}\) with \(n\) wavelengths along the perimeter of a circle of radius \(a_{\psi}\), a radiation peak occurs as \(a_{\psi}\) move to a lower energy state \(n\rightarrow n-1\).
\(a_{\psi}\) is driven to a higher value above \(x=\cfrac{\pi \sqrt { 2{ mc^{ 2 } } } }{G}\) by an external field, on its return, it travels below it normal energy state. It loses potential energy continuously, when it passes a resonance point given by (*), it emits an resonance peak. This is not the energy states given by the Schrodinger wave equation of orbiting electrons, they are energy states when two or more particles interacting as waves exist in a cloud of energy density, \(\psi\), from the post "Two Quantum Wells, Quantum Tunneling, \(v_{min}\)" dated 19 Jul 2015.
In particular, the driving field is affecting the inner electron clouds that surrounds the nucleus below the orbiting \(T^{+}\) particles as described in the post "The Rest Are In The Clouds" dated 16 Apr 2016.
The following table is the X ray emission data using high energy electron bombardment,
\(a_{\psi}1\) and \(a_{\psi}2\) are calculated data.
The split into \(E\,\alpha1\) and \(E\alpha2\) is consistent with the split in the solution for \(a_{\psi}\) in the post "Two Quantum Wells, Quantum Tunneling, \(v_{min}\)" dated 19 Jul 2015. \(E \beta\) is due to the energy state available at the next lower level, \(N\), where the electron cloud contains \(N\) particles.
We estimate the value of \(N\), the energy state of the electron cloud and \(N+1\) the next higher state after the electron accepts a particle by taking the ratio of,
\(\cfrac{ave.\,E\alpha}{E\beta}=\cfrac{N+1}{N}\)
since,
\(N.2\pi a_{\psi}=\cfrac{c}{f_n}=\lambda_\beta\)
\(\cfrac{\lambda_{\alpha\,\,ave}}{\lambda_{\beta}}=\cfrac{ave.\,E\alpha}{E\beta}=\cfrac{N+1}{N}\)
Using the average value of \(E\alpha1\) and \(E\alpha2\) and \(E\beta\) to find \(a_{\psi1}\) and \(a_{\psi2}\) respectively. And for the inner electron cloud,
\(a_{\psi}=\cfrac{\lambda_{\beta}}{N.2\pi }\)
For \(Cu\),
\(N=9\)
The inner electron cloud has a radius of \(a_{\psi}=0.02447*10^{-10}\)
which is one fifth the size of the atomic radius at 1.45 A. This lead us to the resonance frequency,
\(f_{res}=0.061\cfrac { 299792458 }{ 0.02447*10^{-10}}=7.473*10^{18} Hz=7.473 EHz\)
needed to drive \(a_{\psi}\) to resonance. Given an elementary electron charge of 1.602176565*10^{-19} C, a bombardment at \(f_{res}\) is
\(I_{res}=q_e.f_{res}=1.602176565*10^{-19}*7.473*10^{18}=1.1974 A\)
This radiation due to the excitation of the inner electron clouds is in the \(X\) ray region. If this is true, with \(f_{res}\), \(X\) ray production is safer and cheaper... Hurrah! Just before you electrocute yourself, that's 1.1974 A per electron cloud. Hurrah!
The good news is any integer division of \(f_{res}\) will still set the system into resonance but slowly. For example,
\(f=\cfrac{f_{res}}{1000}\)
will still resonate but has a slow buildup.
Note: As the atomic size increases the inner electron cloud is compressed to a smaller radius.
From the post "A Shield" and "A \(\Psi\) Gun" both dated 27 May 2016,
\(f_{res}=0.061\cfrac { c }{ a_{\psi} }\)
\(a_{\psi}\) is driven to oscillate about \(x=\cfrac{\pi \sqrt { 2{ mc^{ 2 } } } }{G}\). The work done in moving \(\psi\) forward is given by,
\(\int_{\pi-A_w}^{\pi+A_p}{tanh(x)}dx\)
On the return, at position \(x\), \(\psi\) radiates this energy gained. The energy radiated is,
\(X=\int_{\pi-A_w}^{\pi+A_p}{tanh(x)}dx-\int_{\pi-A_w}^{x}{tanh(x)}dx\)
\(X=\left[ ln(cosh(x)) \right] _{ \pi -A_{ w } }^{ \pi +A_{ p } }-\left[ ln(cosh(x)) \right] _{ \pi -A_{ w } }^{ x }\)
\( X=X_{ o }-ln(cosh(x))\)
with, \( X_{ o }=ln(cosh(\pi +A_{ p }))\)
A plot of log(cosh(pi+2))-log(cosh(x)) shows an almost linear decrease in energy radiated given the position \(x=a_{\psi}\),
\(U_{1/2}\) marks the value of \(a_{\psi}\) where work done travelling on the left and right side are equal.
We would also expect an almost linear increase in \(X\) as the amplitude \(A_p\) is increased at any given position, for example \(x=\pi\). ie
\( X_{\pi}=ln(cosh(x_{1/2} +x))-ln(cosh(x_{1/2}))\)
is almost increasing linearly. In addition, when \(a_{\psi}\) drops below
\(n.2\pi f_n a_{\psi}=c\) --- (*)
where the particle(s) is in resonance along \(2\pi a_{\psi}\) with \(n\) wavelengths along the perimeter of a circle of radius \(a_{\psi}\), a radiation peak occurs as \(a_{\psi}\) move to a lower energy state \(n\rightarrow n-1\).
In particular, the driving field is affecting the inner electron clouds that surrounds the nucleus below the orbiting \(T^{+}\) particles as described in the post "The Rest Are In The Clouds" dated 16 Apr 2016.
The following table is the X ray emission data using high energy electron bombardment,
| Element | ave \(E\,\alpha\) | \(E\,\alpha1\) | \(E\,\alpha2\) | \(E\,\beta\) | n | \(a_{\psi}1\) | \(a_{\psi}2\) |
| Cr2,8,13,1 | 2.29100 | 2.28970 | 2.29361 | 2.08487 | 11 | 0.0331517775 | 0.0331858844 |
| Fe2,8,14,2 | 1.93736 | 1.93604 | 1.93998 | 1.75661 | 10 | 0.0308378963 | 0.0310675679 |
| Co2,8,15,2 | 1.79026 | 1.78897 | 1.79285 | 1.62079 | 10 | 0.0284964345 | 0.0286654428 |
| Cu2.8.18.1 | 1.54184 | 1.54056 | 1.54439 | 1.39222 | 9 | 0.0272691257 | 0.0277007991 |
| Mo2,8,18,13,1 | 0.71073 | 0.70930 | 0.71359 | 0.63229 | 8 | 0.0141412915 | 0.0143778083 |
\(a_{\psi}1\) and \(a_{\psi}2\) are calculated data.
The split into \(E\,\alpha1\) and \(E\alpha2\) is consistent with the split in the solution for \(a_{\psi}\) in the post "Two Quantum Wells, Quantum Tunneling, \(v_{min}\)" dated 19 Jul 2015. \(E \beta\) is due to the energy state available at the next lower level, \(N\), where the electron cloud contains \(N\) particles.
We estimate the value of \(N\), the energy state of the electron cloud and \(N+1\) the next higher state after the electron accepts a particle by taking the ratio of,
\(\cfrac{ave.\,E\alpha}{E\beta}=\cfrac{N+1}{N}\)
since,
\(N.2\pi a_{\psi}=\cfrac{c}{f_n}=\lambda_\beta\)
\(\cfrac{\lambda_{\alpha\,\,ave}}{\lambda_{\beta}}=\cfrac{ave.\,E\alpha}{E\beta}=\cfrac{N+1}{N}\)
Using the average value of \(E\alpha1\) and \(E\alpha2\) and \(E\beta\) to find \(a_{\psi1}\) and \(a_{\psi2}\) respectively. And for the inner electron cloud,
\(a_{\psi}=\cfrac{\lambda_{\beta}}{N.2\pi }\)
For \(Cu\),
\(N=9\)
The inner electron cloud has a radius of \(a_{\psi}=0.02447*10^{-10}\)
which is one fifth the size of the atomic radius at 1.45 A. This lead us to the resonance frequency,
\(f_{res}=0.061\cfrac { 299792458 }{ 0.02447*10^{-10}}=7.473*10^{18} Hz=7.473 EHz\)
needed to drive \(a_{\psi}\) to resonance. Given an elementary electron charge of 1.602176565*10^{-19} C, a bombardment at \(f_{res}\) is
\(I_{res}=q_e.f_{res}=1.602176565*10^{-19}*7.473*10^{18}=1.1974 A\)
This radiation due to the excitation of the inner electron clouds is in the \(X\) ray region. If this is true, with \(f_{res}\), \(X\) ray production is safer and cheaper... Hurrah! Just before you electrocute yourself, that's 1.1974 A per electron cloud. Hurrah!
The good news is any integer division of \(f_{res}\) will still set the system into resonance but slowly. For example,
\(f=\cfrac{f_{res}}{1000}\)
will still resonate but has a slow buildup.
Note: As the atomic size increases the inner electron cloud is compressed to a smaller radius.
Saturday, October 14, 2017
Sonic Boom
From the post "No Solution But Exit Velocity Anyway" dated 14 Jul 2015,
\(v^{ 2 }_{ { max } }=\cfrac { 1 }{ m } \cfrac { \psi _{ n } }{ \psi _{ max } }\left\{ \psi _{ n }-\psi _{ max } \right\} e^{ \psi _{ max } }\left( { e^{ 2\psi _{ max } }-1 } \right) ^{ 1/2 }\) --- (*)
where \(\psi(x)=-ln(cosh(x-\cfrac{1}{2}x_a)+C\) without scaling both \(x\) and \(y\). With proper scaling,
\(\psi=-i{ 2{ mc^{ 2 } } }\,ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } }(x-x_z)))+c\)
which is the case for the post "Twirl Plus SHM, Spinning Coin" dated 17 Jul 2015. \(-i\) denotes the direction of \(\psi\) and can be ignored as we deal with magnitude here. From that post,
\(\cfrac { \psi _{ d } }{ m } =2{ c^{ 2 } }cos(\theta )ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } x_z))\)
where \(\psi_d=\psi_{max}-\psi_n\) is to oscillate on the surface of \(\psi_{max=77}\) at \(x=x_z\) where
\(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } x_z=3.135009\) and so that,
\(ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } x_z))=2.4438\)
for one charge or one particle.
When we rearrange (*)
\(v^{ 2 }_{ { max } }=-\cfrac { \psi _{ n }-\psi _{ max }}{ m }. \cfrac { \psi _{ n } }{ \psi _{ max } }\ e^{ \psi _{ max } }.\left( { e^{ 2\psi _{ max } }-1 } \right) ^{ 1/2 }\)
\(v^{ 2 }_{ { max } }=-\cfrac { \psi _{ d }}{ m } \cfrac { \psi _{ n } }{ \psi _{ max } }\ e^{ \psi _{ max } }\left( { e^{ 2\psi _{ max } }-1 } \right) ^{ 1/2 }\)
and we set, \(\psi_{max}=\psi(x_z)=ln(cosh(3.135009)=2.4438\), and in both solutions \(n=1\) and \(max=77\)
\(\cfrac { \psi _{ n } }{ \psi _{ max } }=\cfrac{1}{4}.\cfrac{1}{2.4438}\) a constant irrespective of the scaling needed to the \(y-axis\).
We have,
\(v^{ 2 }_{ { max } }=-2{ c^{ 2 } }cos(\theta )*2.4438*\cfrac{1}{4}*\cfrac{1}{2.4438}.e\left( { e^{ 2 }-1 } \right) ^{ 1/2 }\)
because
\(e^{ \psi _{ max } }\left( { e^{ 2\psi _{ max } }-1 } \right) ^{ 1/2 }=e\left( { e^{ 2 }-1 } \right) ^{ 1/2 }\)
as we set \(\psi _{ max }=1\); \(\psi_{max}\) to be one particle.
Therefore,
\(v^{ 2 }_{ { max } }=-c^{ 2 }cos(\theta )*3.4354\)
where the negative sign provides a \(i\) that indicates \(\psi_{n=1}\) escape perpendicular to the radial distance \(x\).
If we apply this to water molecules, assuming that they are sufficiently spherical,
\(cos(\theta )\approx 1\) as \(\theta\approx0\)
The density of water is 1000 kg m-3, and there are a total of ten particles of each type (counting total atomic numbers) per water molecule,
where \(E_{input/proton}\) is the energy density input per particle in a unit volume that would eject a basic particle \(\psi_{n=1}\) or \(\psi_{c}\). We have,
\(E_{input/proton}=\cfrac{1}{2}(one\,\,particle)*c^{ 2 }*(one\,\,unit\,\,volume)*343.54\)
since the particles are already at light speed, \(c\) in the unit volume. We would need to move in \(343.54\) such volume per second. ie at a speed of \(343.54 ms^{-1}\)
For this reason, a sonic boom at the speed of \(343.54 ms^{-1}\).
Don't take this too seriously...
Note: Missing post remains missing. This hopefully replaces the lost post. Each type of particles does not interact with another different type, eg. gravity particles do not interact with protons.
With
\(\theta_{\pi}=3.135009\)
\(\psi_{max}=\psi(x_z)=2mc^2ln(cosh(\theta_{\pi})\) was set to one, ie
\(2mc^2ln(cosh(\theta_{\pi}))=1\)
that corresponds to the definition/observation that \(\psi_{max}\), \(n=77\) is one particle. When the scaling factor \(2mc^2\) is also considered; as we call \(\psi_{max}\) one particle,
\(m=\cfrac{1}{2c^2}*\cfrac{1}{2.4438}=2.2765e-18\)
we have also defined its mass density.
\(v^{ 2 }_{ { max } }=\cfrac { 1 }{ m } \cfrac { \psi _{ n } }{ \psi _{ max } }\left\{ \psi _{ n }-\psi _{ max } \right\} e^{ \psi _{ max } }\left( { e^{ 2\psi _{ max } }-1 } \right) ^{ 1/2 }\) --- (*)
where \(\psi(x)=-ln(cosh(x-\cfrac{1}{2}x_a)+C\) without scaling both \(x\) and \(y\). With proper scaling,
\(\psi=-i{ 2{ mc^{ 2 } } }\,ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } }(x-x_z)))+c\)
which is the case for the post "Twirl Plus SHM, Spinning Coin" dated 17 Jul 2015. \(-i\) denotes the direction of \(\psi\) and can be ignored as we deal with magnitude here. From that post,
\(\cfrac { \psi _{ d } }{ m } =2{ c^{ 2 } }cos(\theta )ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } x_z))\)
where \(\psi_d=\psi_{max}-\psi_n\) is to oscillate on the surface of \(\psi_{max=77}\) at \(x=x_z\) where
\(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } x_z=3.135009\) and so that,
\(ln(cosh(\cfrac { G }{ \sqrt { 2{ mc^{ 2 } } } } x_z))=2.4438\)
for one charge or one particle.
When we rearrange (*)
\(v^{ 2 }_{ { max } }=-\cfrac { \psi _{ n }-\psi _{ max }}{ m }. \cfrac { \psi _{ n } }{ \psi _{ max } }\ e^{ \psi _{ max } }.\left( { e^{ 2\psi _{ max } }-1 } \right) ^{ 1/2 }\)
\(v^{ 2 }_{ { max } }=-\cfrac { \psi _{ d }}{ m } \cfrac { \psi _{ n } }{ \psi _{ max } }\ e^{ \psi _{ max } }\left( { e^{ 2\psi _{ max } }-1 } \right) ^{ 1/2 }\)
and we set, \(\psi_{max}=\psi(x_z)=ln(cosh(3.135009)=2.4438\), and in both solutions \(n=1\) and \(max=77\)
\(\cfrac { \psi _{ n } }{ \psi _{ max } }=\cfrac{1}{4}.\cfrac{1}{2.4438}\) a constant irrespective of the scaling needed to the \(y-axis\).
We have,
\(v^{ 2 }_{ { max } }=-2{ c^{ 2 } }cos(\theta )*2.4438*\cfrac{1}{4}*\cfrac{1}{2.4438}.e\left( { e^{ 2 }-1 } \right) ^{ 1/2 }\)
because
\(e^{ \psi _{ max } }\left( { e^{ 2\psi _{ max } }-1 } \right) ^{ 1/2 }=e\left( { e^{ 2 }-1 } \right) ^{ 1/2 }\)
as we set \(\psi _{ max }=1\); \(\psi_{max}\) to be one particle.
Therefore,
where the negative sign provides a \(i\) that indicates \(\psi_{n=1}\) escape perpendicular to the radial distance \(x\).
If we apply this to water molecules, assuming that they are sufficiently spherical,
\(cos(\theta )\approx 1\) as \(\theta\approx0\)
The density of water is 1000 kg m-3, and there are a total of ten particles of each type (counting total atomic numbers) per water molecule,
\(\cfrac{1}{2}m_{\rho}v^{ 2 }_{ { max } }=E_{input/proton}=\cfrac{1}{2}c^{ 2 }*3.4354*1000*\cfrac{1}{10}\)
where \(E_{input/proton}\) is the energy density input per particle in a unit volume that would eject a basic particle \(\psi_{n=1}\) or \(\psi_{c}\). We have,
\(E_{input/proton}=\cfrac{1}{2}(one\,\,particle)*c^{ 2 }*(one\,\,unit\,\,volume)*343.54\)
since the particles are already at light speed, \(c\) in the unit volume. We would need to move in \(343.54\) such volume per second. ie at a speed of \(343.54 ms^{-1}\)
For this reason, a sonic boom at the speed of \(343.54 ms^{-1}\).
Don't take this too seriously...
Note: Missing post remains missing. This hopefully replaces the lost post. Each type of particles does not interact with another different type, eg. gravity particles do not interact with protons.
With
\(\theta_{\pi}=3.135009\)
\(\psi_{max}=\psi(x_z)=2mc^2ln(cosh(\theta_{\pi})\) was set to one, ie
\(2mc^2ln(cosh(\theta_{\pi}))=1\)
that corresponds to the definition/observation that \(\psi_{max}\), \(n=77\) is one particle. When the scaling factor \(2mc^2\) is also considered; as we call \(\psi_{max}\) one particle,
\(m=\cfrac{1}{2c^2}*\cfrac{1}{2.4438}=2.2765e-18\)
we have also defined its mass density.
Friday, October 13, 2017
Copulins
Now that events leading to mankind's future for the next two centuries have come to pass (this post has nothing to do with it), this is my take on copulins.
Young bees just born are brought before the Queen bee and are assigned to one of approximately nine functional roles in the hive. The Queen bee brushes against the younglings, who are then escorted out to fulfill their newly assigned roles. Some young ones are escorted out of the hive and are killed. It seems that the Queen are able to chemically programmed the young bees. Those who reject her are killed. Bees who later, wake up from their programming are also killed. The point is, there are nine possible chemical variants for each of the nine roles. If we are able to isolate the chemicals and identify the variations we are then closer to deciphering the chemical codes that may apply to us.
The grand assumption is that copulins is that part of us that is insectoid.
The trick is to fool the Queen bee into giving up her chemicals for each role. Maybe a termite queen might be a easier con.
Goodnight.
Young bees just born are brought before the Queen bee and are assigned to one of approximately nine functional roles in the hive. The Queen bee brushes against the younglings, who are then escorted out to fulfill their newly assigned roles. Some young ones are escorted out of the hive and are killed. It seems that the Queen are able to chemically programmed the young bees. Those who reject her are killed. Bees who later, wake up from their programming are also killed. The point is, there are nine possible chemical variants for each of the nine roles. If we are able to isolate the chemicals and identify the variations we are then closer to deciphering the chemical codes that may apply to us.
The grand assumption is that copulins is that part of us that is insectoid.
The trick is to fool the Queen bee into giving up her chemicals for each role. Maybe a termite queen might be a easier con.
Goodnight.
Thursday, October 12, 2017
I Apologize
Some posts are still missing, but I found,
\(\cfrac{1}{\lambda_{p}}=\cfrac{1}{\lambda_{f}}-\cfrac{1}{\lambda_{i}}\)
that follows immediately from,
\(E=h.f=h\cfrac{c}{\lambda}\)
and
\(E_p=E_f-E_i\)
that the photon emitted on a energy state transition, \(n_i\rightarrow n_f\) is the energy difference between the two states.
I will pick up that line of thought yet...
Still, I am missing \(v_{max}=???\). That post is important because it makes the unlikely combination of ice and sonic boom dangerous. Very dangerous.
\(\cfrac{1}{\lambda_{p}}=\cfrac{1}{\lambda_{f}}-\cfrac{1}{\lambda_{i}}\)
that follows immediately from,
\(E=h.f=h\cfrac{c}{\lambda}\)
and
\(E_p=E_f-E_i\)
that the photon emitted on a energy state transition, \(n_i\rightarrow n_f\) is the energy difference between the two states.
I will pick up that line of thought yet...
Still, I am missing \(v_{max}=???\). That post is important because it makes the unlikely combination of ice and sonic boom dangerous. Very dangerous.
Tuesday, October 10, 2017
Planck's Constant Dead
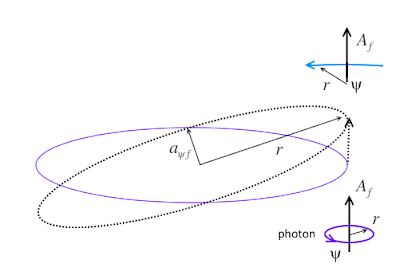
In the case when \(n=1\), as \(\psi\) goes around the radius of the celestial body, \(r=a_{\psi\,f}\), one photon pulse is emitted and between two photons, an EMP.
The frequency is simply,
\(f=\cfrac{c}{2\pi r}=\cfrac{c}{2\pi a_{\psi\,f}}\)
The question of whether photon/EMP emission occurs at at peak \(A_f\), when a transition to \(A_i=0\) results in a collapse of the amplitude, or when at \(A_i\), \(\psi\) returns all a quarter of the period to \(A_f=0\), is still open. Either scenario is possible. Together with the all possible conditions for emission as amplitude, \(A_f\) increases (Post "Pop Now, Pop Later" dated 06 Oct 2017) invites other possible emission frequencies,
\(f=\cfrac{c}{2\pi r}=\cfrac{c}{2\pi a_{\psi\,i}}\)
when \(r=a_{\psi_i}\) is the emission condition. These emitted frequencies do not indicate the difference in energy levels that, on transition between them, leads to the emission. Only when (if) the emission occurs on the criterion of equal perimeter,
\(f=\cfrac{c}{2\pi r}=\cfrac{c}{2\pi \sqrt{2a^2_{\psi\,i}-a^2_{\psi\,f}}}\)
does the expression for frequency/energy of the quanta, photon or EMP, reflect the different between the energy levels as shown by the term,
\(\cfrac{1}{\sqrt{2a^2_{\psi\,i}-a^2_{\psi\,f}}}\)
Notice the factor \(2\) before \(a^2_{\psi\,i}\).
The difference in energy levels, when a emission occurs, also shows up in \(A_n\).
\(A_f=\sqrt{2}\sqrt{a^2_{\psi\,i}-a^2_{\psi\,f}}\)
In the case of of an emission when \(r=a_{\psi\,i}\) where the radius of the elliptical path touches \(a_{\psi\,i}\),
\(A_f=\sqrt{a^2_{\psi\,i}-a^2_{\psi\,f}}\)
These expressions differ by a constant factor of \(\sqrt{2}\). Since,
\(\cfrac{1}{n}=\left(\cfrac{a_{\psi\,c}}{a_{\psi\,n}}\right)^3\)
\(a_{\psi\,n}=\sqrt[3]{n}.a_{\psi\,c}\)
and from the post "Touch And Go" dated 24 Dec 2014,
\(E_{ o }=-mc^{ 2 }\cfrac { 1 }{ a_{ \psi \, i } } \sqrt { \cfrac { (a_{ \psi \, i}-a_{ \psi \, f }) }{ (a_{ \psi \, i }+a_{ \psi \, f }) } }\)
and,
\(E_{ \Delta n }=E_{ o }\sqrt { a^{ 2 }_{ \psi \, i}-a^{ 2 }_{ \psi \, f} }\)
\(E_{ \Delta n }=mc^{ 2 }(\cfrac { a_{ \psi \, f } }{ a_{ \psi \, i } } -1)\)
\(E_{ \Delta n }=mc^{ 2 }(\sqrt[3]{\cfrac{n_f}{n_i}} -1)=mc^{ 2 }(\cfrac{\sqrt[3]{n_f}-\sqrt[3]{n_i}}{\sqrt[3]{n_i}})\)
on a transition from \(n_f\rightarrow n_i\). where \(n_f\) is larger then \(n_i\) when \(a_{\psi\,f}\) is smaller than \(a_{\psi\,i}\). What is this expression about? Consider,
\(f\lambda=c=f_c.2\pi a_{\psi\,c}=f_c.2\pi\cfrac{a_{\psi\,f}}{\sqrt[3]{n_f}}\)
we have,
\(E_{ \Delta n }=mc.f_c.2\pi a_{\psi\,f}\left(\cfrac{\sqrt[3]{n_f}-\sqrt[3]{n_i}}{\sqrt[3]{n_i}\sqrt[3]{n_f}}\right)\)
where \(mc.f_c\) is the rate of change of momentum over one period. It is a force along the orbital path of \(\psi\) and \(2\pi a_{\psi\,f}\) is the total distance along such this path. That is to say,
\(mc.f_c.2\pi a_{\psi\,f}=work\,\,done\)
is the work done along the orbital path as \(\psi\) moves at light speed, \(c\) around an orbit of radius \(a_{\psi\,f}\).
If we set,
\(E=h.f_c\left(\cfrac{\sqrt[3]{n_f}-\sqrt[3]{n_i}}{\sqrt[3]{n_i}\sqrt[3]{n_f}}\right)\)
then,
\(h=mc.2\pi a_{\psi\,f}\)
on a transition from \(n_f\rightarrow n_i\). Given \(n_f\), \(h\) is a constant.
We have this result before. Maybe Planck constant is also dead... 罗刹 of all constants.
The frequency is simply,
\(f=\cfrac{c}{2\pi r}=\cfrac{c}{2\pi a_{\psi\,f}}\)
The question of whether photon/EMP emission occurs at at peak \(A_f\), when a transition to \(A_i=0\) results in a collapse of the amplitude, or when at \(A_i\), \(\psi\) returns all a quarter of the period to \(A_f=0\), is still open. Either scenario is possible. Together with the all possible conditions for emission as amplitude, \(A_f\) increases (Post "Pop Now, Pop Later" dated 06 Oct 2017) invites other possible emission frequencies,
\(f=\cfrac{c}{2\pi r}=\cfrac{c}{2\pi a_{\psi\,i}}\)
when \(r=a_{\psi_i}\) is the emission condition. These emitted frequencies do not indicate the difference in energy levels that, on transition between them, leads to the emission. Only when (if) the emission occurs on the criterion of equal perimeter,
\(f=\cfrac{c}{2\pi r}=\cfrac{c}{2\pi \sqrt{2a^2_{\psi\,i}-a^2_{\psi\,f}}}\)
does the expression for frequency/energy of the quanta, photon or EMP, reflect the different between the energy levels as shown by the term,
\(\cfrac{1}{\sqrt{2a^2_{\psi\,i}-a^2_{\psi\,f}}}\)
Notice the factor \(2\) before \(a^2_{\psi\,i}\).
The difference in energy levels, when a emission occurs, also shows up in \(A_n\).
\(A_f=\sqrt{2}\sqrt{a^2_{\psi\,i}-a^2_{\psi\,f}}\)
In the case of of an emission when \(r=a_{\psi\,i}\) where the radius of the elliptical path touches \(a_{\psi\,i}\),
\(A_f=\sqrt{a^2_{\psi\,i}-a^2_{\psi\,f}}\)
These expressions differ by a constant factor of \(\sqrt{2}\). Since,
\(\cfrac{1}{n}=\left(\cfrac{a_{\psi\,c}}{a_{\psi\,n}}\right)^3\)
\(a_{\psi\,n}=\sqrt[3]{n}.a_{\psi\,c}\)
and from the post "Touch And Go" dated 24 Dec 2014,
\(E_{ o }=-mc^{ 2 }\cfrac { 1 }{ a_{ \psi \, i } } \sqrt { \cfrac { (a_{ \psi \, i}-a_{ \psi \, f }) }{ (a_{ \psi \, i }+a_{ \psi \, f }) } }\)
and,
\(E_{ \Delta n }=E_{ o }\sqrt { a^{ 2 }_{ \psi \, i}-a^{ 2 }_{ \psi \, f} }\)
\(E_{ \Delta n }=mc^{ 2 }(\cfrac { a_{ \psi \, f } }{ a_{ \psi \, i } } -1)\)
\(E_{ \Delta n }=mc^{ 2 }(\sqrt[3]{\cfrac{n_f}{n_i}} -1)=mc^{ 2 }(\cfrac{\sqrt[3]{n_f}-\sqrt[3]{n_i}}{\sqrt[3]{n_i}})\)
on a transition from \(n_f\rightarrow n_i\). where \(n_f\) is larger then \(n_i\) when \(a_{\psi\,f}\) is smaller than \(a_{\psi\,i}\). What is this expression about? Consider,
\(f\lambda=c=f_c.2\pi a_{\psi\,c}=f_c.2\pi\cfrac{a_{\psi\,f}}{\sqrt[3]{n_f}}\)
we have,
\(E_{ \Delta n }=mc.f_c.2\pi a_{\psi\,f}\left(\cfrac{\sqrt[3]{n_f}-\sqrt[3]{n_i}}{\sqrt[3]{n_i}\sqrt[3]{n_f}}\right)\)
where \(mc.f_c\) is the rate of change of momentum over one period. It is a force along the orbital path of \(\psi\) and \(2\pi a_{\psi\,f}\) is the total distance along such this path. That is to say,
\(mc.f_c.2\pi a_{\psi\,f}=work\,\,done\)
is the work done along the orbital path as \(\psi\) moves at light speed, \(c\) around an orbit of radius \(a_{\psi\,f}\).
If we set,
\(E=h.f_c\left(\cfrac{\sqrt[3]{n_f}-\sqrt[3]{n_i}}{\sqrt[3]{n_i}\sqrt[3]{n_f}}\right)\)
then,
\(h=mc.2\pi a_{\psi\,f}\)
on a transition from \(n_f\rightarrow n_i\). Given \(n_f\), \(h\) is a constant.
We have this result before. Maybe Planck constant is also dead... 罗刹 of all constants.
Monday, October 9, 2017
Half Waves And Pulsar
Half wave when \(n=\cfrac{1}{2}\) is just fanciful,
Does it really exist? The point of zero amplitude, where the forward and return path cross is a point from which emission occurs at full amplitude \(A_i\rightarrow A_f\) then \(A_i\rightarrow 0\); where emission occurs when \(\psi\) returns from an elevated state \(A_f\) to \(A_i=0\). \(A_f\) is emitted. In the case of the infinitely small, it may not be noticeable, but on a planetary scale, this big particle will be pulsating when the cross point spins as the big particle spins.
A pulsar!
Does it really exist? The point of zero amplitude, where the forward and return path cross is a point from which emission occurs at full amplitude \(A_i\rightarrow A_f\) then \(A_i\rightarrow 0\); where emission occurs when \(\psi\) returns from an elevated state \(A_f\) to \(A_i=0\). \(A_f\) is emitted. In the case of the infinitely small, it may not be noticeable, but on a planetary scale, this big particle will be pulsating when the cross point spins as the big particle spins.
A pulsar!
Sunday, October 8, 2017
And They All Popped
In the post "Pop Now, Pop Later" dated 06 Oct 2017, the diagrams show \(\psi\) in orbit, the direction of motion was arbitrary. However, since the right hand screw rule was conceived under the notion of conservation of energy, strictly speaking,
A photon is self propelling. An electromagnetic pulse decays. As both direction of rotation are equally probable, emission of a photon or an EMP is equally likely. If a photon is emitted when \(A_f\) is upward, an EMP is released when \(A_f\) is downward as \(\psi\) moves beyond \(pi\) phase.
Which might explain the confusion of photons with \(EMW\)s. They are both emitted for \(n\ge 1\). When \(n=\cfrac{1}{2}\), that \(\psi\) oscillates between space and a time dimension, depending on the direction of \(\psi\), either a photon or an \(EMP\) is emitted with a state transition.
A photon emitting another photon, or an EMP!
If we can influence the direction of \(\psi\) then we can switch the material from a photon emitter to an \(EMP\) emitter and vice versa. Conversely, the presence of photons or \(EMP\)s is indicative of the direction of \(\psi\) when \(n=\cfrac{1}{2}\).
When \(n\ge1\), if \(\psi\) are aligned and uniform, it could be that photons are emitted on one side and \(EMP\)s on the opposite side.
And they all popped.
A photon is self propelling. An electromagnetic pulse decays. As both direction of rotation are equally probable, emission of a photon or an EMP is equally likely. If a photon is emitted when \(A_f\) is upward, an EMP is released when \(A_f\) is downward as \(\psi\) moves beyond \(pi\) phase.
Which might explain the confusion of photons with \(EMW\)s. They are both emitted for \(n\ge 1\). When \(n=\cfrac{1}{2}\), that \(\psi\) oscillates between space and a time dimension, depending on the direction of \(\psi\), either a photon or an \(EMP\) is emitted with a state transition.
A photon emitting another photon, or an EMP!
If we can influence the direction of \(\psi\) then we can switch the material from a photon emitter to an \(EMP\) emitter and vice versa. Conversely, the presence of photons or \(EMP\)s is indicative of the direction of \(\psi\) when \(n=\cfrac{1}{2}\).
When \(n\ge1\), if \(\psi\) are aligned and uniform, it could be that photons are emitted on one side and \(EMP\)s on the opposite side.
And they all popped.
Saturday, October 7, 2017
Elevated Not Excited
When \(A_f\) is elevated but not emitted, the particle remains in a elevated state (not an excited state denoted by \(a_f\) but an elevated state denoted by \(A_f\neq 0\)) until next photon impact drives \(A_f\) beyond the emission threshold and a photon is emitted. As highlighted in the post "Pop Now, Pop Later" dated 06 Oct 2017, it is possible that this photon is emitted when the particle is at the excited energy state (\(a_i\)), or on the particle's return to the lower energy stated at \(a_f\).
But the maximum speed is light speed. The residue energy that remains with the particle results in the wave amplitude not being zero; at \(a_i\), \(A_i\neq 0\) or at \(a_f\), \(A_f\neq 0\). In either case, the particle is in an elevated state. The particle is still restricted to quantized energy states, \(a_n\), but its amplitude \(A_n\) allows for a spread of energy and a mechanism for state transitions.
How does this spread of energy manifest itself?
But the maximum speed is light speed. The residue energy that remains with the particle results in the wave amplitude not being zero; at \(a_i\), \(A_i\neq 0\) or at \(a_f\), \(A_f\neq 0\). In either case, the particle is in an elevated state. The particle is still restricted to quantized energy states, \(a_n\), but its amplitude \(A_n\) allows for a spread of energy and a mechanism for state transitions.
How does this spread of energy manifest itself?
Wrong Direction Scarab UFO
This post corrects the post "A Scarab, A Russian Named Viktor And An UFO" dated 10 Dec 2014. The amplified gravity field should have been upwards.
The tapered coil on the crawl like construct concentrate and amplify the induced gravity field upwards.
The tapered coil on the crawl like construct concentrate and amplify the induced gravity field upwards.
Friday, October 6, 2017
Sapphire Made Of \(T^{-}\)
Sapphire has a density of 3.95–4.03 gcm-3. \(Al_2O_3\) has a density of 3.987gcm-3.
It is likely that in the formation of sapphire, \(Al_2O_3\) is stripped of its other proton layer with twelve paired orbits (three paired orbits from two \(Al\) and nine paired orbits from three \(O\) ), in a barrage of \(T^{-}\) particles. This way density increases. The subsequent \((T^{+},\,T^{-})\) paired orbits bond and form a crystal lattice. Given that the twelve paired orbits is the maximum number of orbits possible with equal angle (63.4o) in 3D space, the lattice formed as the orbits bond is also the maximum variety possible.
Goodnight.
It is likely that in the formation of sapphire, \(Al_2O_3\) is stripped of its other proton layer with twelve paired orbits (three paired orbits from two \(Al\) and nine paired orbits from three \(O\) ), in a barrage of \(T^{-}\) particles. This way density increases. The subsequent \((T^{+},\,T^{-})\) paired orbits bond and form a crystal lattice. Given that the twelve paired orbits is the maximum number of orbits possible with equal angle (63.4o) in 3D space, the lattice formed as the orbits bond is also the maximum variety possible.
Goodnight.
Nothing Pops?
The expression \(r=\sqrt{2a^2_{\psi\,i}-a^2_{\psi\,f}}\) also opens up the possibility that
\(2a^2_{\psi\,i}-a^2_{\psi\,f}\lt 0\)
\(a_{\psi\,f}\gt \sqrt{2}a_{\psi\,i}\) both \(a_{\psi\,i}\) and \(a_{\psi\,f}\) being positive.
In this case, photon emission based on the equal perimeter criterion does not occur. A state transition is likely to be when \(r=a_i\).
It is tempting to set,
\(\cfrac{1}{2}mc^2=E_{\Delta n}=mc^{ 2 }(\cfrac { a_{ \psi \, f } }{ a_{ \psi \, i } } -1)\)
where \(E_{\Delta n}\) as derived in the post "Amplitude, \(A_n\)" dated 23 Dec 2014, is the energy in \(A_f\). And \(m\) is the mass density of the photon. This simply states that the photon is at light speed along \(A_f\). Then,
\(a_{ \psi \, i }=\cfrac{2}{3}a_{ \psi \, f }\)
Of course,
\(a_{ \psi \, f }\gt a_{ \psi \, i }\)
Does this suggest that unless \(a_{ \psi \, i }\lt\cfrac{2}{3}a_{ \psi \, f }\), we have no emission? That the energy states denoted by \(a_{ \psi \, i }\) and \(a_{ \psi \, f }\) must first be sufficiently far apart for photon emissions to occur with a state transition between them?
Any energy state \(a_{\psi\,f}\) above \(a_{\psi\,i}\), where
\(a_{\psi\,i}\lt a_{\psi\,f}\lt \cfrac{3}{2}a_{\psi\,i}\)
is invisible (with no photon emission) when a state transition from \(a_{\psi\,i}\) occurs. Or does it simply mean that photons can be emitted with velocity less than light speed along \(A_f\)?
What happen to \(A_f\) if not emitted?
Pop Now, Pop Later
From the post "Amplitude, \(A_n\)" dated 23 Dec 2014 where it was proposed that the transition to an adjacent state occurs when the amplitude of the wave \(\psi\) has increase to an extend where the perimeter of the resulting elliptical orbit is equal to the circular orbital perimeter of the next state. This perimeter criteria is derived from the fact that \(\psi\) is at constant light speed, when the perimeter of two orbits are the same, then \(\psi\) on both orbits will have the same frequency and thus with Planck's relation (\(E=h.f\)), both will have the same energy.
where,
\(A_f=\sqrt{2}\sqrt{a^2_{\psi\,i}-a^2_{\psi\,f}}\) and
\(r^{ 2 }=2a^2_{\psi\,i}-a^2_{\psi\,f}\)
From the post "Touch And Go" dated 24 Dec 2014, transition to the state associated with \(a_{\psi\,i}\) occurs when the long radius of the ellipse equals \(a_{\psi\,i}\). This occurs before the perimeters of the initial and final states are equal.
where,
\(A_f=\sqrt{a^2_{\psi\,i}-a^2_{\psi\,f}}\) and
\(r=a_{\psi\,i}\)
If the emission of a photon occurs on transition to \(r=\sqrt{2a^2_{\psi\,i}-a^2_{\psi\,f}}\) or \(r=a_{\psi\,i}\), and \(\psi\) thereafter orbit at \(r=\sqrt{2a^2_{\psi\,i}-a^2_{\psi\,f}}\) or \(r=a_{\psi\,i}\) with amplitude \(A_i=0\), the energy in \(A_f\) can be associated with the translation energy of the photon and, the oscillatory component of this wave (photon as a wave) is respectively \(r=\sqrt{2a^2_{\psi\,i}-a^2_{\psi\,f}}\) or \(r=a_{\psi\,i}\).
It could also be,
that the emission of a photon occurs only after \(\psi\) returns to \(a_{\psi\,f}\); after a timer interval \(t\), having traveled along the elliptical path a quarter of the way at light speed, \(c\). In this case, the emitted photon has a oscillatory component at \(a_{\psi\,f}\) only.
Which one of these occur? The emitted photon is at \(\sqrt{2a^2_{\psi\,i}-a^2_{\psi\,f}}\), \(a_{\psi\,i}\) or \(a_{\psi\,f}\). If there is a constraint on \(A_f\), below a threshold for which no emission occurs then all three possible scenarios can occur in different settings. All three photons at their respective energies \(E\) can be detected.
\(E=h.\cfrac{2\pi.a_{\psi}}{c}\)
What would be the constraint on \(A_f\)? Goodnight.
where,
\(A_f=\sqrt{2}\sqrt{a^2_{\psi\,i}-a^2_{\psi\,f}}\) and
\(r^{ 2 }=2a^2_{\psi\,i}-a^2_{\psi\,f}\)
From the post "Touch And Go" dated 24 Dec 2014, transition to the state associated with \(a_{\psi\,i}\) occurs when the long radius of the ellipse equals \(a_{\psi\,i}\). This occurs before the perimeters of the initial and final states are equal.
\(A_f=\sqrt{a^2_{\psi\,i}-a^2_{\psi\,f}}\) and
\(r=a_{\psi\,i}\)
It could also be,
that the emission of a photon occurs only after \(\psi\) returns to \(a_{\psi\,f}\); after a timer interval \(t\), having traveled along the elliptical path a quarter of the way at light speed, \(c\). In this case, the emitted photon has a oscillatory component at \(a_{\psi\,f}\) only.
Which one of these occur? The emitted photon is at \(\sqrt{2a^2_{\psi\,i}-a^2_{\psi\,f}}\), \(a_{\psi\,i}\) or \(a_{\psi\,f}\). If there is a constraint on \(A_f\), below a threshold for which no emission occurs then all three possible scenarios can occur in different settings. All three photons at their respective energies \(E\) can be detected.
\(E=h.\cfrac{2\pi.a_{\psi}}{c}\)
What would be the constraint on \(A_f\)? Goodnight.
Tuesday, October 3, 2017
Diamond Is Silicon Not Carbon
Silicon has a density of 2.3290 g/cm3 and diamond has a density of 3.515 g/cm3. Could it be that all four paired orbits in the outer proton layer of \(Si\) have been stripped and in their place \(T^{-}\) particles terminates the nucleus core. Effectively an \(C\) isotope with an outer most \((T^{+}, T^{-})\) layer of four paired orbits (each \(p^{+}\) particle held by the weak field from a \(T^{+}\) particle being replaced with a \(T^{-}\)). These paired orbits bond with four other similar isotopes at the corners of a tetrahedron and forms the diamond lattice.
A stripped \(Si\) lattice cell will be smaller and so when packed into a lattice, the resulting crystal has a higher density.
Diamond is Silicon not Carbon.
If this is true, diamond can be formed by bombarding \(Si\) crystal with \(T^{-}\) particles and at the same time removing the freed electric charges by applying an electric potential end to end.
A stripped \(Si\) lattice cell will be smaller and so when packed into a lattice, the resulting crystal has a higher density.
Diamond is Silicon not Carbon.
If this is true, diamond can be formed by bombarding \(Si\) crystal with \(T^{-}\) particles and at the same time removing the freed electric charges by applying an electric potential end to end.
Monday, October 2, 2017
Artificial Rubies
If clear crystal are bonded by temperature particles, where the intermolecular (interatomic) bonds that holds the crystal together involve only \(T^{+}\) and \(T^{-}\) particles, then either the nuclei so bonded lose the outer \(p^{+}\) layer or gain a \(g^{+}\) and a \(T^{+}\) layer.
In the former case and in the case of atomic crystal unit cells, the nulcei would have transmuted to an element one left along a horizontal period of the periodic table. A crystal made from \(Cu\), behave like \(Ni\) in the lattice.
In the former but in the case of molecular crystal unit cells, the molecule quasi nucleus as a whole loses one \(p^{+}\) layer. The final "transmuted" molecule is that which appears as the chemical composition associated with the crystal. For example ruby, \(Al_2O_3:Cr\) gives the transmuted repeating unit of the crystal. \(AlSiO_3\) is the simplest likely starting molecule. The \(AlSi\) pair loses a singular unpaired proton layer that is above the three paired oxygen, \(O\) proton orbits. The exposed \(T^{+}\) orbit that previously provided for the weak field that held the escaped proton acquires a \(T^{-}\) particle and pairs up with another unit. The paired \((T^{+}, T^{-})\) bond links up with other paired units and we have a crystal lattice.
\(AlSi\) is above \(O_3\), when the crystal collapses as in the case of magnetite (post "Split, Stir And Charged" dated 17 Aug 2017), \(O_3\rightarrow Cr \), Chromium is formed.
If this is true, to form Ruby we have to first help the lone outer proton in \(Al_2O_3\) to escape and then cools it with \(T^{-}\) particles and lastly encourage the paired \((T^{+}, T^{-})\) bonds re-orientate and link up into a lattice.
Bloody hell, not. \(AlSi\) has an extra \(g^{+}\) particle that cannot be removed without also removing the \(T^{+}\) particle that forms crystal bonds. The crystal unit is with an isotope of \(Al\) and is denser (more mass as the result of one more \(g^{-}\) particles that balance the \(g^{+}\) particle in the nucleus) than natural ruby.
Natural ruby without an isotopes and without the resulting density anomaly is likely to have a quasi nuclei \(Al_2O_3\) that has acquired first an extra \(g^{+}\) layer followed by a \(T^{+}\) layer.
What about diamonds?
In the former case and in the case of atomic crystal unit cells, the nulcei would have transmuted to an element one left along a horizontal period of the periodic table. A crystal made from \(Cu\), behave like \(Ni\) in the lattice.
In the former but in the case of molecular crystal unit cells, the molecule quasi nucleus as a whole loses one \(p^{+}\) layer. The final "transmuted" molecule is that which appears as the chemical composition associated with the crystal. For example ruby, \(Al_2O_3:Cr\) gives the transmuted repeating unit of the crystal. \(AlSiO_3\) is the simplest likely starting molecule. The \(AlSi\) pair loses a singular unpaired proton layer that is above the three paired oxygen, \(O\) proton orbits. The exposed \(T^{+}\) orbit that previously provided for the weak field that held the escaped proton acquires a \(T^{-}\) particle and pairs up with another unit. The paired \((T^{+}, T^{-})\) bond links up with other paired units and we have a crystal lattice.
\(AlSi\) is above \(O_3\), when the crystal collapses as in the case of magnetite (post "Split, Stir And Charged" dated 17 Aug 2017), \(O_3\rightarrow Cr \), Chromium is formed.
If this is true, to form Ruby we have to first help the lone outer proton in \(Al_2O_3\) to escape and then cools it with \(T^{-}\) particles and lastly encourage the paired \((T^{+}, T^{-})\) bonds re-orientate and link up into a lattice.
Bloody hell, not. \(AlSi\) has an extra \(g^{+}\) particle that cannot be removed without also removing the \(T^{+}\) particle that forms crystal bonds. The crystal unit is with an isotope of \(Al\) and is denser (more mass as the result of one more \(g^{-}\) particles that balance the \(g^{+}\) particle in the nucleus) than natural ruby.
Natural ruby without an isotopes and without the resulting density anomaly is likely to have a quasi nuclei \(Al_2O_3\) that has acquired first an extra \(g^{+}\) layer followed by a \(T^{+}\) layer.
What about diamonds?
Bouncing Astronaut
I was reading...
A set of parallel mirrors were launched into space and set in motion in the direction parallel to the planes of the mirrors. Light bouncing between the mirrors at constant light speed takes a longer time interval between bounce as the mirrors move at higher velocity. The motion of the mirrors adds a displacement component along its direction of travel. Light instead of just bouncing perpendicularly between the mirrors has to travel along this direction of motion also.
This has nothing to do with gravity! The setup might as well be on earth and the result is the same. There was no need to go into outer space.
The time interval taken as light bounce between the mirrors was used to "measure" time. It was said that since this interval increases as the mirrors speed up, time itself slows down. And the astronaut with the mirrors aged slowly.
A set of parallel mirrors were launched into space and set in motion in the direction parallel to the planes of the mirrors. Light bouncing between the mirrors at constant light speed takes a longer time interval between bounce as the mirrors move at higher velocity. The motion of the mirrors adds a displacement component along its direction of travel. Light instead of just bouncing perpendicularly between the mirrors has to travel along this direction of motion also.
This has nothing to do with gravity! The setup might as well be on earth and the result is the same. There was no need to go into outer space.
The time interval taken as light bounce between the mirrors was used to "measure" time. It was said that since this interval increases as the mirrors speed up, time itself slows down. And the astronaut with the mirrors aged slowly.
Light bouncing off mirrors has nothing to do with the astronaut aging unless the astronaut is also bouncing off the mirrors and each time he hits a mirror he dies a little. In this case, the longer it takes between consecutive bounce the less he aged. Ouch..., Ouch..., Ouch... compared to Ouch, Ouch, Ouch.
In a gravity field, without the action of any force, as an object increases in velocity in space (KE for PE), its speed in time decreases.
\(v^2_t+v^2_s=c^2\) --- (*)
where \(v_t\) is the object velocity in time, \(v_s\) is its velocity in space and \(c\) is a constant.
Energy across the time and space dimensions is conserved. In this way, time as experienced by the object slows. The gravity field here is incidental, the object could be likewise accelerating in a temperature field or an electric field without the action of an applied contact force.
If there is an applied force from an engine, is energy still conserved? No. Does time speed slow? No, (*) does not apply.
And life goes on, Ouch...