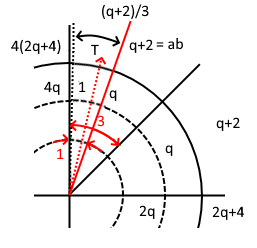
From previously, "Going Around In Circle" dated 09 Jan 2023, \(3\) has been excluded as a factor of \(q+2\),
the total number of integer marks along arc \(q+2\) from \(1\) to \(\cfrac{q+2}{3}\) is about,
\(T=\cfrac{q+2}{3}-1+1\)
after removing \(1\) and \(2\) as possible intercepts,
\(T=\cfrac{q+2}{3}-3+1=\cfrac{q+2}{3}-2=\cfrac{q-4}{3}\)
and the number of possible 1st intercept lines from arc \(q\) and below is,
\(a=\cfrac{q-1}{2}-2=\cfrac{q-5}{2}\)
where arcs \(1\) and \(2\) are excluded. There is more targets than arrows, and the numbers \(2\), \(3\), \(4\) and \(5\) are involved.
The targets are evenly spaced along arc \(q+2\) at equal angle intervals, \(\cfrac{\pi}{2}*\cfrac{1}{2}*\cfrac{1}{q+2}=\cfrac{\pi}{4(q+2)}\),
\(\cfrac{3\pi}{4(q+2)}\),\(\cfrac{4\pi}{4(q+2)}\), \(\cfrac{5\pi}{4(q+2)}\)... \(\cfrac{(q+2)\pi}{3*4(q+2)}=\cfrac{\pi}{12}\) excluded.
\(\cfrac{\pi}{4}\cfrac{3}{(q+2)}\),\(\cfrac{\pi}{4}\cfrac{4}{(q+2)}\), \(\cfrac{\pi}{4}\cfrac{5}{(q+2)}\)... \(\cfrac{\pi}{4}\cfrac{(q+1)}{3*(q+2)}\)
whereas the arrows are at,
\((\cfrac{\pi}{4}*\cfrac{1}{3})\) excluded, \((\cfrac{\pi}{4}*\cfrac{1}{5})\), \((\cfrac{\pi}{4}*\cfrac{1}{7})\), \((\cfrac{\pi}{4}*\cfrac{1}{9})\)... \((\cfrac{\pi}{4}*\cfrac{1}{q-2})\)
Removing \(\cfrac{\pi}{4}\) the common factor,
\(\cfrac{3}{(q+2)}\),\(\cfrac{4}{(q+2)}\), \(\cfrac{5}{(q+2)}\)... \(\cfrac{(q+1)}{3}*\cfrac{1}{(q+2)}\)
\(\cfrac{1}{5}\), \(\cfrac{1}{7}\), \(\cfrac{1}{9}\)... \(\cfrac{1}{q-2}\)
If these two series share a common member, then \(q+2\) is not prime.
This is nothing new, as a prime candidate is often tested for all possible factors. These members are on the delimited line,
\(\cfrac{1}{q+2} x\)
and \(3\le x\le \cfrac{q+1}{3}\)
and the curve,
\(\cfrac{1}{x}\)
but for \(x\) odd, \(5\le x\le (q-2)\)
If the line and the curve intersect within the specified domains at integer points then \(q+2\) is not prime.
The target are on a line and the arrows on a reciprocal curve. They will meet once, but do they meet in the restricted domains? The line maybe translated along the \(x\) axis, as any coincidental member on the two series will fail \(q+2\) as a prime.
The line and curve will meet, but not necessarily on odd integer points, but always, no matter how large \(q\) is, as the curve is translated along the \(x\) axis within its domain in odd integer steps,\(5\le x\le (q-2)\).
Integers that are candidates for factors will be below the curve \(\cfrac{1}{x}\) when the line starts at the origin. As the line translated along \(x\) in odd integer steps, candidates that are not factors are moved above the curve.
Factors will meet on the curve exactly.
Good morning.