For Twins Large

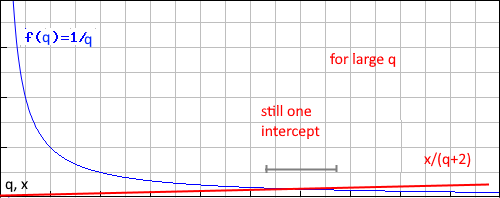
 There is still just one intercept at a time, as the line is translated by odd steps (start on odd number plus 2 for every next step).

The two low gradients might guarantee an odd integer intercepts.  This suggests twin primes cease to exist beyond this point.

Twin prime conjecture is wrong.  Even if the twin prime returns and then start off again, some regions along the primes number will not have twin primes series.

If the target points on \(1/q\) were to straighten out, there is still no guarantee that there will be a intersect at an integer on \(1/q\).

So, when there is no integer intercept， twin primes occurs over long stretches where \(1/q\) levels off, then the \(1/q\) asymptote drops and factors appear, the twin prime disappears over a short period, afterwards, the asymptote levels off again and twin primes occur again over a relatively long period.  Over long plateau of the asymptote either no twin primes or consecutive twin primes can occur.  This is followed by a drop in the asymptote and once again a series of twin primes or not can occur.  The drop in asymptote usher a change but can change to the same.