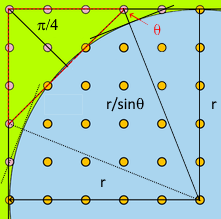
Consider again,
\(\theta_0=\cfrac{\pi}{4}\)
\(Area = r(\cfrac{1}{sin\theta_0}-1).r(\cfrac{1}{sin\theta_0}-1)tan\theta_0=r^2(\cfrac{1}{sin\theta_0}-1)^2tan\theta_0\)
For all four quadrant, multiply by \(M_0=4\).
Consider the next triangle for which there are two,
\(\theta_1=\cfrac{1}{2}(\pi-(\cfrac{\pi}{2}-\theta_0))=\cfrac{\pi}{4}+\cfrac{\theta_0}{2}=\cfrac{3}{8}\pi\)
\(Area = r(\cfrac{1}{sin\theta_1}-1).r(\cfrac{1}{sin\theta_1}-1)tan\theta_1=r^2(\cfrac{1}{sin\theta_1}-1)^2tan\theta_1\)
\(M_1=4*2\)
And the next \(\theta_2\),
\(\theta_2=\cfrac{1}{2}(\pi-(\cfrac{\pi}{2}-\theta_1))=\cfrac{\pi}{4}+\cfrac{\theta_1}{2}=\cfrac{7}{16}\pi\)
We have,
\(S_{\theta_2}=\cfrac{\pi}{4}+\cfrac{1}{2}\left(\cfrac{\pi}{4}+\cfrac{\theta_0}{2}\right)=\cfrac{\pi}{4}+\cfrac{1}{2}*\cfrac{\pi}{4}+\cfrac{\theta_0}{2^2}\)
\(S_{\theta_3}=\cfrac{\pi}{4}+\cfrac{1}{2}\left(\cfrac{\pi}{4}+\cfrac{1}{2}\left(\cfrac{\pi}{4}+\cfrac{\theta_0}{2}\right)\right)=\cfrac{\pi}{4}+\cfrac{\pi}{2*4}+\cfrac{\pi}{2^2*4}+\cfrac{\theta_0}{2^3}\)
\(S_{\theta_4}=\cfrac{\pi}{4}+\cfrac{1}{2}\left(\cfrac{\pi}{4}+\cfrac{\pi}{2*4}+\cfrac{\pi}{2^2*4}+\cfrac{\theta_0}{2^3}\right)=\cfrac{\pi}{4}+\cfrac{\pi}{2*4}+\cfrac{\pi}{2^2*4}+\cfrac{\pi}{2^3*4}+\cfrac{\theta_0}{2^4}\)
In general,
\(S_{\theta_i}=\cfrac{\pi}{2^2}+\cfrac{\pi}{2^3}+\cfrac{\pi}{2^4}+...+\cfrac{\pi}{2^{i+1}}+\cfrac{\theta_0}{2^{i}}\)
Multiplicative factor due to symmetry, \(M_2=4*2^2=16\), in general for \(\theta_i\),
\(M_i=4*2^{i}=2^{i+2}\)
We have a series \(E_i\) to estimate \(\pi\), with \(r=1\), area of square 4,
\(\epsilon_i=M_i(\cfrac{1}{sin\theta_i}-1)^2tan\theta_i\)
\(\theta_0=\cfrac{\pi}{4}\)
\(S_{\theta_i}=\cfrac{\pi}{2^2}+\cfrac{\pi}{2^3}+...+\cfrac{\pi}{2^{i+1}}+\cfrac{\theta_0}{2^{i}}=\cfrac{\pi}{2^2}+\cfrac{\pi}{2^3}+...+\cfrac{\pi}{2^{i+2}}\)
and \(M_i=2^{i+2}\)
\(E_i=4-\epsilon_0-\epsilon_1-\epsilon_2...-\epsilon_i\)
\(E_0=8(\sqrt{2}-1)=3.313708\)
\(\epsilon_1=8(\cfrac{1}{sin(\frac{\pi}{4}+\frac{\pi}{8})}-1)^2tan(\frac{\pi}{4}+\frac{\pi}{8})=0.131111\)
\(E_1=8(\sqrt{2}-1)-0.131111=3.182598\)
\(\epsilon_2=16(\cfrac{1}{sin(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16})}-1)^2tan(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16})=0.03087297\)
\(E_2=8(\sqrt{2}-1)-0.131111-0.03087297=3.151725\)
\(\epsilon_3=32(\cfrac{1}{sin(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16}+\frac{\pi}{32})}-1)^2tan(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16}+\frac{\pi}{32})\\=0.0076065\)
\(E_3=8(\sqrt{2}-1)-0.131111-0.03087297-0.0076065=3.144118\)
\(\epsilon_4 =64(\cfrac{1}{sin(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16}+\frac{\pi}{32}+\frac{\pi}{64})}-1)^2tan(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16}+\frac{\pi}{32}+\frac{\pi}{64}) \\=0.001894755\)
\(E_4=8(\sqrt{2}-1)-0.131111-0.03087297-0.0076065-0.001894755=3.1422236\)
\(\epsilon_5 =128(\cfrac{1}{sin(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16}+\frac{\pi}{32}+\frac{\pi}{64}+\cfrac{\pi}{128})}-1)^2tan(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16}+\frac{\pi}{32}+\frac{\pi}{64}+\cfrac{\pi}{128}) \\=0.000473261\)
\(E_5=8(\sqrt{2}-1)-0.131111-0.03087297-0.0076065-0.001894755-0.000473261\\=3.1417500\)
\(\epsilon_6 =256(\cfrac{1}{sin(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16}+\frac{\pi}{32}+\frac{\pi}{64}+\frac{\pi}{128}+\frac{\pi}{256})}-1)^2tan(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16}+\frac{\pi}{32}+\frac{\pi}{64}+\frac{\pi}{128}+\frac{\pi}{256}) \\=0.000118288\)
\(E_6=8(\sqrt{2}-1)-0.131111-0.03087297-0.0076065-0.001894755\\-0.000473261-0.000118288=3.1416317\)
Just for fun. \(\pi\) as a simple series.