No, sum of the reciprocals of primes is not the count of primes,
\(\pi(x)\ne log(x)\)
but,
\(\sum^n_{i=1}\cfrac{1}{p_n}\rightarrow log(n)\)
more correctly, piecewise,
\(\sum^n_{i}\cfrac{1}{p_n}\rightarrow log(x)|^{n}_{i}\)
for \(n\) and \(i\) large, positive. Which adds no information because, the sum of \(\cfrac{1}{x}\) is smaller than the integration of \(\cfrac{1}{x}\), ie \(log(x)\). And rightfully,
\(p_n=n\)
which means a log(x) factor is the result of possible intersections of \(\cfrac{1}{x}\) with \(\cfrac{x}{p_n+2}\).
Shifting \(\cfrac{x}{p_n+2}\) against \(\cfrac{1}{x}\) to find an integer intercept is,
\(\cfrac{x_1}{p_n+2}=y=\cfrac{1}{x_2}\)
\(x_1x_2=p_n+2\)
looking for a product of \(x_1\) and \(x_2\), that rules out \(p_n+2\) as prime.
There is still no new information that makes prime \(p_n\) different from any number \(x\).
If \(\pi(x)\lt log(x)\) that the number of primes up to \(x\) is bounded by \(log(x)\), and not \(x/log(x)\) there are way less primes available for anything and everything.
\(\pi(x)\lt log(x)\)
This is serious, Prime Scarce.
It's \(\pi(x)=log(x)\) and not \(\cfrac{x}{log(x)}\) and \(p_n=n\) and not \(nlog(n)\),
Earth is a dynamic system spinning and revolving, a space elevator no matter how weightless,
will topple the system and end up spinning along the equator, albeit a new equator. When that happens, there will be huge tidal waves, flooding and drastic climate changes. So, don't build a space elevator anywhere else except exactly at the equator.
From the previous post "Zero Error Small Piece Of Pi" dated 11 Jan 2023, that series for \(\pi\) has a zero correction at the infinite term, that means the infinite but one term represents \(\pi\) fully, and \(\pi\) is rational. Eventually.
Neither \(e\) nor \(\sqrt{2}\) share this. Both their descending series representations tend to zero at the infinite term but not quite zero.
A new kind of irrationality.
The fact is,
\(\theta_0=\cfrac{\pi}{4}\)
\(S_{\theta_i}=\cfrac{\pi}{2^2}+\cfrac{\pi}{2^3}+...+\cfrac{\pi}{2^{i+1}}+\cfrac{\theta_0}{2^{i}}=\cfrac{\pi}{2^2}+\cfrac{\pi}{2^3}+...+\cfrac{\pi}{2^{i+2}}\)
\(S^{i\rightarrow\infty}_{\theta_i}=\cfrac{\pi}{2^2}(1+\cfrac{1}{2}+\cfrac{1}{2^2}+...+\cfrac{1}{2^{i}}...)\)
\(S^{i\rightarrow\infty}_{\theta_i}=\cfrac{\pi}{2^2}(2)\)
\(S^{i\rightarrow\infty}_{\theta_i}=\cfrac{\pi}{2}\)
So, the last correction is,
\(\epsilon_{i\rightarrow\infty}=M_{i\rightarrow\infty}(\cfrac{1}{sin\theta_{i\rightarrow\infty}}-1)^2tan\theta_{i\rightarrow\infty}\)
\(\epsilon_{i\rightarrow\infty}=M_{i\rightarrow\infty}(\cfrac{1}{sin(\frac{\pi}{2})}-1)^2tan(\frac{\pi}{2})=0\)
no matter what \(M_{i\rightarrow\infty}\) and \(tan(\frac{\pi}{2})\) are. The smallest piece of \(\pi\) corrected is zero.
Consider again,
\(Area = r(\cfrac{1}{sin\theta_0}-1).r(\cfrac{1}{sin\theta_0}-1)tan\theta_0=r^2(\cfrac{1}{sin\theta_0}-1)^2tan\theta_0\)
For all four quadrant, multiply by \(M_0=4\).
Consider the next triangle for which there are two,
\(\theta_1=\cfrac{1}{2}(\pi-(\cfrac{\pi}{2}-\theta_0))=\cfrac{\pi}{4}+\cfrac{\theta_0}{2}=\cfrac{3}{8}\pi\)
\(Area = r(\cfrac{1}{sin\theta_1}-1).r(\cfrac{1}{sin\theta_1}-1)tan\theta_1=r^2(\cfrac{1}{sin\theta_1}-1)^2tan\theta_1\)
\(M_1=4*2\)
And the next \(\theta_2\),
\(\theta_2=\cfrac{1}{2}(\pi-(\cfrac{\pi}{2}-\theta_1))=\cfrac{\pi}{4}+\cfrac{\theta_1}{2}=\cfrac{7}{16}\pi\)
We have,
\(S_{\theta_2}=\cfrac{\pi}{4}+\cfrac{1}{2}\left(\cfrac{\pi}{4}+\cfrac{\theta_0}{2}\right)=\cfrac{\pi}{4}+\cfrac{1}{2}*\cfrac{\pi}{4}+\cfrac{\theta_0}{2^2}\)
\(S_{\theta_3}=\cfrac{\pi}{4}+\cfrac{1}{2}\left(\cfrac{\pi}{4}+\cfrac{1}{2}\left(\cfrac{\pi}{4}+\cfrac{\theta_0}{2}\right)\right)=\cfrac{\pi}{4}+\cfrac{\pi}{2*4}+\cfrac{\pi}{2^2*4}+\cfrac{\theta_0}{2^3}\)
\(S_{\theta_4}=\cfrac{\pi}{4}+\cfrac{1}{2}\left(\cfrac{\pi}{4}+\cfrac{\pi}{2*4}+\cfrac{\pi}{2^2*4}+\cfrac{\theta_0}{2^3}\right)=\cfrac{\pi}{4}+\cfrac{\pi}{2*4}+\cfrac{\pi}{2^2*4}+\cfrac{\pi}{2^3*4}+\cfrac{\theta_0}{2^4}\)
In general,
\(S_{\theta_i}=\cfrac{\pi}{2^2}+\cfrac{\pi}{2^3}+\cfrac{\pi}{2^4}+...+\cfrac{\pi}{2^{i+1}}+\cfrac{\theta_0}{2^{i}}\)
Multiplicative factor due to symmetry, \(M_2=4*2^2=16\), in general for \(\theta_i\),
\(M_i=4*2^{i}=2^{i+2}\)
We have a series \(E_i\) to estimate \(\pi\), with \(r=1\), area of square 4,
\(\epsilon_i=M_i(\cfrac{1}{sin\theta_i}-1)^2tan\theta_i\)
\(\theta_0=\cfrac{\pi}{4}\)
\(S_{\theta_i}=\cfrac{\pi}{2^2}+\cfrac{\pi}{2^3}+...+\cfrac{\pi}{2^{i+1}}+\cfrac{\theta_0}{2^{i}}=\cfrac{\pi}{2^2}+\cfrac{\pi}{2^3}+...+\cfrac{\pi}{2^{i+2}}\)
and \(M_i=2^{i+2}\)
\(E_i=4-\epsilon_0-\epsilon_1-\epsilon_2...-\epsilon_i\)
\(E_0=8(\sqrt{2}-1)=3.313708\)
\(\epsilon_1=8(\cfrac{1}{sin(\frac{\pi}{4}+\frac{\pi}{8})}-1)^2tan(\frac{\pi}{4}+\frac{\pi}{8})=0.131111\)
\(E_1=8(\sqrt{2}-1)-0.131111=3.182598\)
\(\epsilon_2=16(\cfrac{1}{sin(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16})}-1)^2tan(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16})=0.03087297\)
\(E_2=8(\sqrt{2}-1)-0.131111-0.03087297=3.151725\)
\(\epsilon_3=32(\cfrac{1}{sin(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16}+\frac{\pi}{32})}-1)^2tan(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16}+\frac{\pi}{32})\\=0.0076065\)
\(E_3=8(\sqrt{2}-1)-0.131111-0.03087297-0.0076065=3.144118\)
\(\epsilon_4 =64(\cfrac{1}{sin(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16}+\frac{\pi}{32}+\frac{\pi}{64})}-1)^2tan(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16}+\frac{\pi}{32}+\frac{\pi}{64}) \\=0.001894755\)
\(E_4=8(\sqrt{2}-1)-0.131111-0.03087297-0.0076065-0.001894755=3.1422236\)
\(\epsilon_5 =128(\cfrac{1}{sin(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16}+\frac{\pi}{32}+\frac{\pi}{64}+\cfrac{\pi}{128})}-1)^2tan(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16}+\frac{\pi}{32}+\frac{\pi}{64}+\cfrac{\pi}{128}) \\=0.000473261\)
\(E_5=8(\sqrt{2}-1)-0.131111-0.03087297-0.0076065-0.001894755-0.000473261\\=3.1417500\)
\(\epsilon_6 =256(\cfrac{1}{sin(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16}+\frac{\pi}{32}+\frac{\pi}{64}+\frac{\pi}{128}+\frac{\pi}{256})}-1)^2tan(\frac{\pi}{4}+\frac{\pi}{8}+\frac{\pi}{16}+\frac{\pi}{32}+\frac{\pi}{64}+\frac{\pi}{128}+\frac{\pi}{256}) \\=0.000118288\)
\(E_6=8(\sqrt{2}-1)-0.131111-0.03087297-0.0076065-0.001894755\\-0.000473261-0.000118288=3.1416317\)
Just for fun. \(\pi\) as a simple series.
Consider the circle,
and the estimate for the number of integer points in the circle is, square minus four triangles.
\(e_z=(2r)^2-4(r(\sqrt{2}-1))^2\)
\(e_z=4r^2(1-(\sqrt{2}-1)^2)\)
\(e_z=4r^2(1-(2+1-2\sqrt{2})\)
\(e_z=8r^2(\sqrt{2}-1)\)\(\pi\) need not get involved, but the estimation comes from a circle in a square.
Good night.
These are frequencies for Fusobacterium infection including the eyes,
Fusobacterium Infection 470-12 377-91 115-7 Hz
Fusobacterium Infection 470-12 377-91 115-7 177-979 1779-79 Hz
Fusobacterium Infection 115-7 Hz
Fusobacterium Infection 377-91 Hz
Fusobacterium Infection 470-12 Hz
Good luck.
There is still just one intercept at a time, as the line is translated by odd steps (start on odd number plus 2 for every next step).
Twin prime conjecture is wrong. Even if the twin prime returns and then start off again, some regions along the primes number will not have twin primes series.
If the target points on \(1/q\) were to straighten out, there is still no guarantee that there will be a intersect at an integer on \(1/q\).
So, when there is no integer intercept， twin primes occurs over long stretches where \(1/q\) levels off, then the \(1/q\) asymptote drops and factors appear, the twin prime disappears over a short period, afterwards, the asymptote levels off again and twin primes occur again over a relatively long period. Over long plateau of the asymptote either no twin primes or consecutive twin primes can occur. This is followed by a drop in the asymptote and once again a series of twin primes or not can occur. The drop in asymptote usher a change but can change to the same.
More accurately,
which does not indicate the inevitability of \(q+2\) being prime.
No prove.
From previously, "Going Around In Circle" dated 09 Jan 2023, \(3\) has been excluded as a factor of \(q+2\),
the total number of integer marks along arc \(q+2\) from \(1\) to \(\cfrac{q+2}{3}\) is about,
\(T=\cfrac{q+2}{3}-1+1\)
after removing \(1\) and \(2\) as possible intercepts,
\(T=\cfrac{q+2}{3}-3+1=\cfrac{q+2}{3}-2=\cfrac{q-4}{3}\)
and the number of possible 1st intercept lines from arc \(q\) and below is,
\(a=\cfrac{q-1}{2}-2=\cfrac{q-5}{2}\)
where arcs \(1\) and \(2\) are excluded. There is more targets than arrows, and the numbers \(2\), \(3\), \(4\) and \(5\) are involved.
The targets are evenly spaced along arc \(q+2\) at equal angle intervals, \(\cfrac{\pi}{2}*\cfrac{1}{2}*\cfrac{1}{q+2}=\cfrac{\pi}{4(q+2)}\),
\(\cfrac{3\pi}{4(q+2)}\),\(\cfrac{4\pi}{4(q+2)}\), \(\cfrac{5\pi}{4(q+2)}\)... \(\cfrac{(q+2)\pi}{3*4(q+2)}=\cfrac{\pi}{12}\) excluded.
\(\cfrac{\pi}{4}\cfrac{3}{(q+2)}\),\(\cfrac{\pi}{4}\cfrac{4}{(q+2)}\), \(\cfrac{\pi}{4}\cfrac{5}{(q+2)}\)... \(\cfrac{\pi}{4}\cfrac{(q+1)}{3*(q+2)}\)
whereas the arrows are at,
\((\cfrac{\pi}{4}*\cfrac{1}{3})\) excluded, \((\cfrac{\pi}{4}*\cfrac{1}{5})\), \((\cfrac{\pi}{4}*\cfrac{1}{7})\), \((\cfrac{\pi}{4}*\cfrac{1}{9})\)... \((\cfrac{\pi}{4}*\cfrac{1}{q-2})\)
Removing \(\cfrac{\pi}{4}\) the common factor,
\(\cfrac{3}{(q+2)}\),\(\cfrac{4}{(q+2)}\), \(\cfrac{5}{(q+2)}\)... \(\cfrac{(q+1)}{3}*\cfrac{1}{(q+2)}\)
\(\cfrac{1}{5}\), \(\cfrac{1}{7}\), \(\cfrac{1}{9}\)... \(\cfrac{1}{q-2}\)
If these two series share a common member, then \(q+2\) is not prime.
This is nothing new, as a prime candidate is often tested for all possible factors. These members are on the delimited line,
\(\cfrac{1}{q+2} x\)
and \(3\le x\le \cfrac{q+1}{3}\)
and the curve,
\(\cfrac{1}{x}\)
but for \(x\) odd, \(5\le x\le (q-2)\)
If the line and the curve intersect within the specified domains at integer points then \(q+2\) is not prime.
The target are on a line and the arrows on a reciprocal curve. They will meet once, but do they meet in the restricted domains? The line maybe translated along the \(x\) axis, as any coincidental member on the two series will fail \(q+2\) as a prime.
Integers that are candidates for factors will be below the curve \(\cfrac{1}{x}\) when the line starts at the origin. As the line translated along \(x\) in odd integer steps, candidates that are not factors are moved above the curve.
Factors will meet on the curve exactly.
Good morning.
Since a dodecahedron cannot be divided along its edges into two like a tetrahedron, it seem that only positive particles are possible.
Going somewhere.
The presence of \(q\) does not guarantee that \(q+2\) is prime.
\(q+2=a*b\)
if \(a\) is not an integer neither \(a\) nor \(b\) is a factor of \(q+2\).
\(q\) is prime means none of the 1st intercept lines (lines through the first mark and the center of the arc) below it, cross it at an integer marking.
The first mark intercept lines approaches the vertical as the arc value approach \(2q\).
The first mark intercept from arc \(2q\) will be very close to the first mark of \(2(q+2)\).
The widest 1st mark comes from \(q=3\) or an arc of length \(6\). If this 1st intercept line crosses on \(R_a\) on arc \(2(q+2)\)then the integer marks between the first mark on arc \(2(q+2)\) and \(R_a\) will have no intercepts from all first mark intercept from arcs below it, when \(q+2\) is prime.
The arc \(2q=6\) divides the right angle in \(\cfrac{\pi}{12}\) this angle extends a width,
\(\cfrac{\pi}{12}*\cfrac{2}{\pi}2(q+2)=\cfrac{1}{3}(q+2)\)
on arc \(2(q+2)\).
So, \(q+2\) is prime only if there are no intercepts from its third mark to the \(\cfrac{1}{3}(q+2)\) mark due to all 1st mark intercept lines below it.
This narrows the range from which a factor of \(q+2\) can be found, to a number up to \(\cfrac{1}{3}(q+2)\) after considering the number \(3\).
All numbers above arc \(b=3\) will mark, with a 1st intercept line, to the left of the 1st intercept line from \(b=3\), and narrows the range from which a factor can be found.
Only \(b\) that are odd are considered.
The 1st intercept steps in decreasing step angle given by \(\cfrac{\pi}{4b}\).
The step angle size of \(q\) is \(\cfrac{\pi}{4q}\). If, an integer marking at \(n\), intercepts with the first intercept line from arc \(b\).
\(n\cfrac{\pi}{4q}=\cfrac{\pi}{4b}\)
then \(q=nb\)
then \(q\) has a factor \(n\), and \(b\).
There is no further information to indicate \(q+2\) to be prime.
The length of phosphorus-oxygen double bonds is \(1.52\,\dot{A}\)
\(f_{res}=0.122\cfrac{c}{BL}\)
\(f_{res}=0.122*\cfrac{299792458}{1.52}*10^{10}\)
\(\cfrac{f_{res}}{10^{15}}= 240.622\,\,Hz\)
This frequency will hopefully change the functional group to a tautomer P(OH)3 attached compound. And render toxins like Sarin, Tabun and VX ineffective.
Other phosphorous bonds breakable,
Phosphorus-oxygen single bonds,
\(f_{res}=0.122*\cfrac{299792458}{1.66}*10^{10}\)
\(\cfrac{f_{res}}{10^{15}}= 220.329\,\,Hz\)
or with the involvement of d orbitals,
\(f_{res}=0.122*\cfrac{299792458}{1.62}*10^{10}\)
\(\cfrac{f_{res}}{10^{15}}= 225.769\,\,Hz\)
Dephosphorylation deactivates proteins and is very dangerous.
Take your time,
Particle assignments and then Platonic Solids assignments,
Whatever the assignment one particle pair, force/energy type is missing.
\(C^+\), \(C^-\) for life force, Chi. Chronos, actually. Time particles/photons.
Maybe to amplify the number of negative particles, a frequency of \(141.988\,kHz\) will drive more particles outwards.
This is a \(T^{+}\) source, a complete encased octahedron,
it renders things more colorful and with enough strength, combusts them.
This is a \(T^{-}\) source, a half encased octahedron, shorted at the base,
it turns things invisible and at high strength crystalizes them. Things made invisible can be illuminated by the encased tetrahedron shown above. A beam of this nature is deflected by crystalline surfaces.
\(p^+\), \(e^-\), \(g^+\), \(g^-\), \(m^+\), \(m^-\) and space.
Just enough Platonic Solids; but which is which. Can a negative source be amplified without making them positive,
is there more negative particles or do the particles increase in size and turn positive.
Hydrogen Chloride bond length is, \(1.275\,\dot{A}\)
\(f_{res}=0.122\cfrac{c}{BL}\)
\(f_{res}=0.122*\cfrac{299792458}{1.275}*10^{10}\)
\(\cfrac{f_{res}}{10^{15}}= 286.860\,\,Hz\)
Hydrogen Chloride 286-86 2868-60 Hz
Just in case you have poison in your drinks.
If superimposed dimension count as such higher dimensions and there can be three orthogonal axes in 3D space the last providing chirality.
There are two other dimensions in space and then three in time, for a total of five possible dimensions to superimpose on. Including the mandate (un-imposed), that we exist in, five superimpose dimensions and six existing dimensions for a total of thirteen dimensions.
One higher dimension is three space plus time superimposed on another one dimension.
Superposition will explain how particles are made to radiate photons.
They started as a superposition of a photon and a particle in the first place. Orthogonality restricts the types of superposition possible and so limits the types of photons emitted or not at all.
If this,
\(\cfrac{\partial^2\psi}{\partial\,t^2_c}=ic\cfrac{\partial^2\psi}{\partial\,x\partial\,t_c}\)
can accommodate another, \(\cfrac{\partial}{\partial\,t}\) or \(\cfrac{\partial}{\partial\,x}\), then that is higher dimension.
Nothing else.
Then again, there might be a new type of energy that can be drawn from the time dimension,
In which case, we have two types of electrons, both almost massless because of missing or oscillating \(t_g\). An oscillating field can be subjected to a similar field and displays a bias that is observed as a small mass/inertia. Without \(t_g\), massless, would mean a wave; a pure wave.
This might destroy wave-particle duality. Wave and particles are separate entity with the similar field properties.
And there's a lot more types of particles.
If \(t_c\) is also oscillating then there are two wave/particle superimposed in a orthogonal direction. And this beast,
\(\cfrac{\partial^2\psi}{\partial\,t^2_c}=ic\cfrac{\partial^2\psi}{\partial\,x\partial\,t_c}\)
is sleeping with,
\(i\cfrac{\partial^2\psi}{\partial\,t^2_m}=-c\cfrac{\partial^2\psi}{\partial\,x\partial\,t_m}\)
in an orthogonal manner, \(i*i=-1\).
Four types of energy (Platonic Solids) can be drawn from the time dimension, (a believe, not science) in different combinations of a wave creates different particles. Particle may superimpose orthogonally and manifest as different distinctive particles with different (superimposed) properties.
Those with \(t_g\), gravitational energy are particles with mass, those with oscillating \(t_g\) display small mass under gravitational field. The rest (absolutely no \(t_g\)) are photons for the time being.
Good night.
Remember this model of an electron,
where \(t_g\) in oscillation results in a particle without mass. But this field is manifested/ produced in rotation.
This is magnetism. An electron in circular motion, produce magnetic field lines that is actually gravitational field lines. This way temperature acts independently. Magnetism does not exist, it is just gravity fields; magnetic monopoles do not exist.
This would explain,
This arrangement brings control upwards and downwards. Slow the spin of the top disc and the contraption lifts; slow down the spin of the bottom disc and the contraption lowers.
Open the disc in the direction of intended travel and the contraption move forward in that direction.
Or, bring the disc closer in the direction of intended travel and the contraption move forward in that direction.
A rational diagonal is easier to draw, \(c=\cfrac{a}{b}\) means a line \(b\) on the x axis and \(a\) up on the y axis; a line through cutting the both axes at these point is \(c\). But what else?
The effect of not allowing other numbers for \(c\) is an incomplete set of spaced ellipses.
But what look like a ellipse is an ellipse. Since every ellipse can be drawn on a pixelized computer screen, there are finite number of rational points on every ellipse. Birch and Swinnerton-Dyer conjecture is half proven!
The latter part of the Conjecture, "...and the first non-zero coefficient in the Taylor expansion of L(E, s) at s = 1 is given by more refined arithmetic data attached to E over K", suggests an irrational coefficient, possibly involving \(\sqrt{2}\) and \(\pi\).
Dithering is after the ellipse has been drawn. A kind of fuzz to made the lines smooth.
A made-up question to plot ellipse on cartesian points. Not fun.
Note: \(c\) is used to general the ellipse; rational \(c\), plots rational points on the ellipse. If \(c\) not rational move diagonal to next rational points and start there.
When the square full right angle triangle divided by the repeated factor, \(2\). It seem an area of size \(1\) square unit does not count,
There are not considered squares there! And apparently, a lot of unit squares are being cut up to fit into a right angle triangle.
What childhood memories.
Prime are not congruent, by their definition! This is wrong.
When \(a=1\), for
\(b=2n\)
Area of triangle\(=\cfrac{1}{2}a*b=\cfrac{1}{2}.2n=n\)
But side \(c\) must also be rational.
\(\sqrt{1^2+(2n)^2}=\sqrt{4n^2+1}\)
which is the square of an odd number. \(c\) is odd.
\(\sqrt{4n^2+1}=2m+1\)
\(4n^2+1=(2m+1)^2\)
\(n=\cfrac{1}{4}\sqrt{(2m+1)^2-1}\)
So, maybe...
\(b=2n=\cfrac{1}{2}\sqrt{(2m+1)^2-1}\)
\(c=2m+1\)
\(a=1\)
This unfortunately does not happen. \(a=1\) only is wrong. Both is possible, \(a=odd\), \(b=even\) and \(c=odd\). Both sides \(a\) and \(b\) being even is not allow because they will generate a \(\sqrt{2}\) factor in \(c\) unless they form a perfect square. A pair of \(a\) and \(b\) both odd will give even \(c\) s. A pair of \(a\), \(b\), odd and even, will given odd \(c\) s.
But what about fractions? odd, even fraction?
In seem that this question is didactic, Kindergarten all over again. Aliens teachers...
Thank you.
This is why they are squares in rational right angle triangle,
\(\cfrac{1}{2}*\cfrac{204}{3}*\cfrac{6}{3}=68=2*2*17\)
the squares comes from multiple factors, in this case \(2*2\).
Note: \({\cfrac{204}{3},\,\cfrac{6}{3}}\) also work for an area of 51 which has no square and so squareless.
This is why the elliptic,
More likely every curve has more than one, such set.
Because this can fly,
so, this can fly better,
$$y^{-i2ln(a)/\pi}=a^{\frac{1}{n}}$$
$$e^{i\theta-i2ln(a)/\pi}=a^{\frac{1}{n}}$$
This is wrong! So have been,
$$\LARGE{e^{(i\theta)^{-i2ln(a)/\pi}=\,\LARGE{{a}^{\small\frac{1}{n}}}}}$$
Which is bad...
$$\LARGE{e^{{(i\theta)^{-i2ln(a)/\pi}}=\,\LARGE{{a}^{\small\frac{1}{n}}}}}$$
$$\LARGE{e^{{(ie)^{-i2ln(\theta)ln(a)/\pi}}=\,\LARGE{{a}^{\small\frac{1}{n}}}}}$$
$$\LARGE{e^{{(i^i)^{-2ln(\theta)ln(a)/\pi}.(e)^{-i2ln(\theta)ln(a)/\pi}}=\,\LARGE{{a}^{\small\frac{1}{n}}}}}$$
$$\LARGE{e^{{(i^i)^{-2ln(\theta)ln(a)/\pi}}.e^{-i2ln(\theta)ln(a)/\pi}=\,\LARGE{{a}^{\small\frac{1}{n}}}}}$$
\(\theta=\cfrac{\pi}{2n}\), and \(i^i=0.20788\lt 1\)
What about,
$$\LARGE{e^{(i^i)^{-\frac{2}{\pi}ln(a+\frac{\pi}{2n})}}}$$
$$\LARGE{e^{e^{-i\frac{2}{\pi}ln(a+\frac{\pi}{2n})}}}$$
And what the f**k for?
$$\LARGE{|a^{\frac{1}{n}}|=e^{(i^i)^{-\frac{2}{\pi}ln(a+\frac{\pi}{2n})}}}.{e^{{cos\left(\frac{2}{\pi}ln(a+\frac{\pi}{2n})\right)}}}$$
Since the imaginary part has is a sine function,
$$-1 \le \angle arg\le 1$$
and as only positive values are considered, and the stated condition,
$$\cfrac{1}{m}+\cfrac{1}{n}+\cfrac{1}{k}\lt 1$$
$$|\angle arg |\lt 1$$
Still not going to heaven.
Looking at,
\(c^k= e^{-i\cfrac{\pi}{2k}}. c^{i\cfrac{\pi}{2}}\) This is wrong.
Consider,
\(y=c^{i\cfrac{\pi}{2}}\)
\(ln(y)=i\cfrac{\pi}{2}ln(c)\)
\(y=c.e^{i\cfrac{\pi}{2}}\)
\(c^k= c.e^{i\cfrac{\pi}{2}\left(1-\cfrac{1}{k}\right)}\)
Visually,
With \(|c|\rightarrow \infty\), \(c\) goes to heaven, upwards.
And it seem that,
\(a^{\frac{1}{m}}+b^{\frac{1}{n}}=c^\frac{1}{k}\)
is just,
\(cos(\theta_m)+cos(\theta_n)=cos(\theta_k)\), where the radius of the circle has been normalized with a factor \(\cfrac{\pi}{2}\).
\(r\theta_n=arc_n\) , \(r=\cfrac{2}{\pi}\)
\(\theta_n=\cfrac{1}{n}\cfrac{\pi}{2}\)
\(\theta_m=\cfrac{1}{m}\cfrac{\pi}{2}\)
\(\theta_k=\cfrac{1}{k}\cfrac{\pi}{2}\)
\(cos(\cfrac{\pi}{2m})+cos(\cfrac{\pi}{2n})=cos(\cfrac{\pi}{2k})\)
What happened to \(a^{m}, b^{n}, c^{k}\)?
$${ln(y)nln(a)}=\frac{\pi}{2}ln(a)$$
Consider, $$y=e^{i\theta}$$
$$ln(y)=i\cfrac{1}{n}\cfrac{\pi}{2}$$
$$\cfrac{2ln(y)ln(a)}{\pi}=i\frac{1}{n}ln(a)$$
$$ln(y)nln(a)=i\frac{\pi}{2}ln(a)$$
$$ln(y)=ln(a)(\frac{i\pi}{2}-n)$$
$$e^{i\theta}=a^{\cfrac{i\pi}{2}-n}$$
$$a^n=e^{-i\theta} a^{\cfrac{i\pi}{2}}$$
And so,
$$a^m=e^{-i\theta_m} a^{\cfrac{i\pi}{2}}$$
$$b^n=e^{-i\theta_n} a^{\cfrac{i\pi}{2}}$$
$$c^k=e^{-i\theta_k} a^{\cfrac{i\pi}{2}}$$
With \(\theta_n=\cfrac{\pi}{2n}\), \(\theta_m=\cfrac{\pi}{2m}\), \(\theta_k=\cfrac{\pi}{2k}\)
$$a^m+b^n=e^{-i\cfrac{\pi}{2n}}. a^{i\cfrac{\pi}{2}}+e^{-i\cfrac{\pi}{2m}} .b^{i\cfrac{\pi}{2}}=e^{-i\cfrac{\pi}{2k}}. c^{i\cfrac{\pi}{2}}=c^k$$
And they just keep turning.
If we define a cross product as, \(a\otimes b=b^a\)
consider,
\(\frac{1}{m}\otimes a = a^{\frac{1}{m}}\)
\(\frac{1}{n}\otimes b = b^{\frac{1}{n}}\)
\(\frac{1}{k}\otimes c = c^{\frac{1}{k}}\)
and
\(c^\frac{1}{k}=a^{\frac{1}{m}}+b^{\frac{1}{n}}\)
where \(\cfrac{1}{m}+\cfrac{1}{n}+\cfrac{1}{k}\lt 1\)
Are \(\frac{1}{m}\), \(\frac{1}{n}\) and \(\frac{1}{k}\) confined strictly within the space of a one eighth of a sphere of radius \(r=\frac{2}{\pi}\) (surface of sphere not included)? Yes. As required.
This will have finite numbers of triplets, \((a^m,\,b^n,\,c^k)\) but their values can be high.
Does \(a\), \(b\) and \(c\) being co-prime make them (their axes) orthogonal here? As illustrated, positive and orthogonal.
\(\{\frac{1}{k},\,c\}\), is defined on the plane extended by \((\frac{1}{n}\otimes b)\) and \((\frac{1}{m}\otimes a)\). The cross product \((\frac{1}{k}\otimes c)\) lift \(\{\frac{1}{k},\,c\}\) into a perpendicular plane. \((\frac{1}{m}\otimes a)\), \((\frac{1}{n}\otimes b)\) and \((\frac{1}{k}\otimes c)\) forms a rectangular axis, right handed.
What happen to the angle in between with cross product?
It is in \(\cfrac{1}{n}\), etc in actual \(\cfrac{1}{n}\) should be represented by a vector,
\(\cfrac{2}{\pi}e^{i\theta}\), where \(\theta=\cfrac{1}{n}\cfrac{\pi}{2}\) the arc length \(\cfrac{1}{n}\) divided by the radius, \(\cfrac{2}{\pi}\). This radius constant is in all \(a\), \(b\) and \(c\) and cancels eventually in the equation,
\(a^m+b^n=c^k\)
Consider, $$y=e^{i\theta}$$
$$ln(y)=i\cfrac{1}{n}\cfrac{\pi}{2}$$
$$-i\cfrac{2ln(y)ln(a)}{\pi}=\frac{1}{n}ln(a)$$
$$y^{-i2ln(a)/\pi}=a^{\frac{1}{n}}$$
$$e^{i\theta-i2ln(a)/\pi}=a^{\frac{1}{n}}$$
$$e^{i\theta}a^{-i2/\pi}=a^{\frac{1}{n}}$$ This is wrong.
$$e^{i\theta}=a^{\frac{1}{n}+i2/\pi}$$
$$Re[e^{i\theta}]=cos(\theta)=a^{\frac{1}{n}}$$
This is where \(cos(\theta)\) for the cross product is hiding.
This means the illustration is consistent. Fermat–Catalan Conjecture, on hold.
In the previous post "Looking For P4?" dated 02 Dec 2023, the arc \(P1+P2+2\) is not excluded from providing a \(q\). This \(q=1\), and \(P3=P1+P2+2-2=P1+P2\).
And there is no need for full lower arcs, just long enough to provide the first integer marking.
This is how arc \(P1+P2-2\) provides a possible solution always,
Possibly,
\(P4=P1-2\), \(P3=P2+2\)
or
\(P4=P1+2\), \(P3=P2-2\)
when the radial intersects arc \(P1+P2+2\) and recovers 4 integer units in total.
Before, in the case of Beal Conjecture, \(q\), the scaling factor, is a factor of \(C^z\), in this case however \(q\) need not be a factor of \(P1+P2+2\).
\(q_1\) and \(q_2\) are selected when the line through the 1 mark on a lower arc meets the arc \(P1+P2+2\) on a integer mark. These \(q_n\) are primes. \(P4\) is then,
\(P4=1.q_1\) or
\(P4=1.q_2\)
Only on the first integer marking on arc \(n\) is the factor \(P4=1.q_n\), a possible candidate for \(P4\). All other distances along the lower arcs will not provide a prime factor. \(a.p_n\), \(b.p_n\)... etc, are not prime.
\(P3\) is obtained by \(P3=P1+P2+2-P4\). If it is not a prime number, find the next \(p_n\).
Where is the \(\cfrac{1}{\pi}\) factor often encountered? It is hidden in the radius.
Thank you very much, for your Ps and Qs.
Note: The first integer mark from the vertical is always available no matter what \(a\) introduced in the previous post "Missing The Mark Goldbach" dated 02 Jan 2023, is.
The bisector divides \(P1+P2-n\) into two odd numbers. \(q\) is odd. Only odd number are considered in turn as factor/primes.
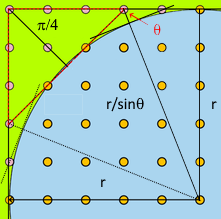
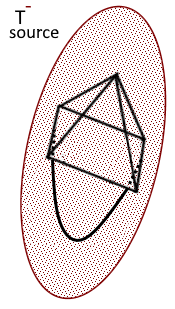
Consider two primes, \(P1\) and \(P2\), we construct a quadrant with an arc ABC and another arc EFG. These arcs are of length.
arc ABC\(=P1+P2\) and
arc EFG\(=P1+P2+2\)
Both arcs are divided by its length to give integer points and provide markings, each of unit length \(1\),
Since there is symmetry about the bisector of the arcs, only one portion is discuss here. Since, \(P1+P2\) is even, this portion is always odd.
Let \(m+n=P1+P2\)
and
\(j+k=P3+P4=P1+P2+2\)
Consider,
\(\cfrac{P2}{P1+P2}=\cfrac{P3}{P1+P2+2}\)
\(P3=\cfrac{P1+P2+2}{P1+P2}P2=\cfrac{n}{n+m}(P1+P2+2)\)
\(\cfrac{k}{j+k}=\cfrac{P3}{(P1+P2+2)}=\cfrac{n}{n+m}\)
So,
\(\cfrac{1}{j+k}=\left(\cfrac{n}{k}\right)\cfrac{1}{n+m}\)
since \(n\lt k\)
the unit division along \((j+k)\) is a fraction of the unit division along \((n+m)\). \(P1\) is not a factor of \(P4\) and \(P2\) is not a factor of \(P3\).
In fact, given that the length of arc EFG is just one plus the length of arc ABC. This gain in a unit division is spread over the length of EFG There is no line through the origin that will meet both markings on ABC and EFG.
If a line OF is drawn from an integer mark on EFG, this line will not intersect with any integer mark on ABC. This is true for any marking on EFG, and so for all values of \(P4\). A missed integer marking means the obtained value is not an integer; it is not a valid value.
Also since, arc EFG has length,
arc EFG\(=P1+P2+2\)
and the lower arcs have length \(P1+P2\), \(P1+P2-2\)... ...\(6\),\(4\),\(2\)
There is a possible \(a\gt 1\), such that
\({P1+P2+2}=a\overset{ \frown}L\)
where \(\overset{ \frown}L\) is the length of a lower arcs.
\(\cfrac{1}{\overset{ \frown}L}=a.\cfrac{1}{P1+P2+2}\)
The unit markings on arc L is of multiple unit width on arc EFG.
A line OF through an integer point on this lower arc \(\overset{ \frown}L\) will cross another integer point along EFG. This would mean \(P4\) has a factor (like P1) on \(\overset{ \frown}L\), given by this intersection.
Consecutive marking on this lower arc L will intersect EFG at \(a\) spacing apart. That means there are \(a-2\) choices of \(P4\) for an \(a\) size aperture on EFG that do not have this factor.
\(a\) decreases with with longer arc length L. The choice of \(P4\) to avoid an integer marking on L also decreases. With a lower arc length of \(2\) that accommodates for the case \(P4=P3\), there are at most \((P1+P2-2)-2+1\),\(P1+P2-2\) (odd numbers discarded) possible values of \(a\) (every lower arc provides a factor and is avoided), excluded are \(L=(P1+P2)\) that provides no factors and \(L=1\). So, there is at least one choice on arc EFG that allows line OF to avoid all integer intersections on the lower arcs. (The one choice on arc of length \(P1+P2-2\) when all lower arcs have factors).
That means \(P4\) can have no factors. \(P4\) can be prime. The primes \(P1\) and \(P2\) guarantee that there is at least one choice of \(P4\) to be prime. The arc ABC allows line OF to sweep for all integer on EFG, to obtain a value for \(P4\) that is prime.
When \(P4\) is prime, and by symmetry \(P3\) is also prime (swap \(P3\) with \(P4\)). For \(P3\), start at the horizontal instead, line OF missing all markings on lower arcs. It is the same line when \(P4\) was discussed.
So, given two primes, \(P1\) and \(P2\) the sum of which is \(P1+P2\), there are then \(P3\) and \(P4\), such that the next integer,
\(P1+P2+2=P3+P4\)
and both \(P3\) and \(P4\) are prime.
So by induction, given that \((1+1=2)\), \((2+1=3)\), \((3,1=4)\) and \((3+2=5)\) all even numbers can be represented as the sum of two primes.
Goldbach's Conjecture is proven.
Note:
Factors found using this graphical method divide \(P3\), \(P4\) and their sum \(P3+P4=P1+P2+2\).
If OF crosses with integer markings on EFG and any of the lower arcs L, then a factor is found on L. That cannot happen. \(P1+P2+2\) cannot be divided. This derivation does not choose \(P4\) and \(P3\).
Starting from an integer marking on arc L, but the line OF misses integer markings on arc EFG, means \(P4\) and \(P3\) are not integers. Starting from an integer marking on EFG, but the line OF misses integer markings on L, means the lower arc does not provide a factor to both \(P4\) and \(P3\) and \(P1+P2+2\). Not just \(P4\). This graphical method find factors for \(P4\), \(P3\) and their sum \(P3+P4=P1+P2+2\).
Only experiment and persistent will tell. A much safer way to turn invisible than stuffing olive into your navel.
Happy New Year.
This does work because it seem that one \(q\) fits all, \(n_{j}\), \(n_{j+1}\)...
There seems to be no simple math problem now. But maybe all higher composite numbers share all factors, prime or otherwise, from lower composite numbers, as the graph above suggests.
They do, but is just \(2\) for the series \(2n_{j}\), \(2n_{j+1}\)...
To used the graphical method from (post "Beal And Integer Quadrant Arcs" dated 31 Dec 2022), we plot \(A^x=n_{j}\), \(B^y=1\) and \(C^z=n_{j}+1\). Any irreducible factor wholly divides \(n_{j}\) and is a prime factor of \(n_{j}\).
At first it seem, this graphical method to find factors that disallows other factors when a prime factor is plotted, would discontinue Grimm series of \(n_j\) immediately.
However, for the integer \(n_{j+k}=4n_{j}+3\) with arc \(4(4n_{j}+3+1)=16(n_{j}+1)\), the arc \(4(n_{j}+1)\) suggest a factor \(4\).
What? Ignore this line when doing arc \(4n_{j}+3\)?
