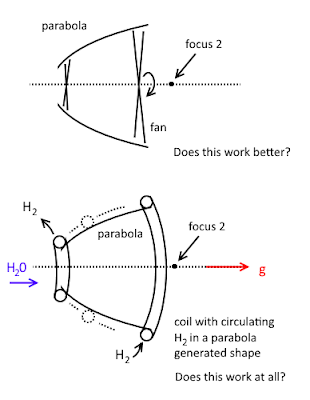
With the second focus,
The reasoning is that from Einstein's equivalence principle that the mass of an object obtained from gravity observations is the same mass when the object is subjected to a force, then it is postulated here that force-interactions are gravitational in nature and are due to gravity particles and gravitational energy density \(\psi\). This \(\psi\) can be made to distribute in a parabola profile such that the term,
\(\cfrac{\partial^2\psi}{\partial x^2}=0 \)
at a focus point, such that in the expression,
\(\cfrac{\partial \psi}{\partial x}\cfrac{\partial \psi}{\partial t}=\cfrac{c^2p}{\sqrt{2}}.\cfrac{\partial^2\psi}{\partial x^2}.e^{-i\pi/4}\)
from the post "My Own Wave equation", dated 20 Nov 2014, the solution for \(\cfrac{\partial \psi}{\partial t}\) is without an explicit phase lag, \(e^{-i\pi/4}\).
Notice that in the case of a jet engine in the top diagram, the second focus point is beyond the fan axial.
Do they work?